🖥 خوارزميات أساسية في تعلم الآلة

هذا المنشور هو ترجمة (حرفية) للفصل الثالث “لكتاب المائة صفحة في تعليم الآلة” من تأليف أندري بوركوف.

الفصل الثالث: خوارزميات أساسية

في هذا الفصل، سنشرح خمس خوارزميات ليست فقط هي الأكثر شهره ولكن أيضاً إما تكون هي الأكثر فاعليه أو تستخدم كجزء من أجزاء خوارزميات أخرى.

الإنحدار الخطي

يعتبر الإنحدار الخطي من أشهر خوارزميات الإنحدار والذي يتشكل فيه النموذج بشكل خطي بناءاً على الخصائص المدخله فيه.

مشكلة

لدينا مجموعه من الأمثله المصنفة $\{(x_{i},y_{i})\}_{i=1}^{n}$، هنا $N$ هو حجم المجموعة، $x_{i}$ هي أبعاد متجه الخواص للمثال $i=1 ... N$، $y_{i}$ هو رقم صحيح والهدف $(y_{i} \in R)$ وكل خاصية $x_{i} ^{(j)}, j = 1 ... D$ هي رقم صحيح أيضاً.

نريد أن نبني نموذج $f_{w,b} (x)$ بشكل خطي من الخصائص المعطاه في المثال $x$:

$$f_{w,b} (x) = wx + b$$ المعادلة (1)

فيها $w$ عبارة عن متجه $D$-الأبعاد من المدخلات، $b$ هي رقم صحيح و $wx$ هي ضرب نقطي. الرمز $f_{w,b}$ يعني ان النموذج $f$ لديه مدخلين: $w$ و $b$. سنستخدم النوذج لنتوقع $y$ المجهولة للمعطى $x$ كالتالي: $y = f_{w,b} (x)$. نموذجين يعطون مدخلين اثنين $(w,b)$ سيخرجون على الأرجح توقعين اثنين إذا تمت تجربتهما على نفس المثال. نريد إيجاد النتائج الأمثل $(w*,b*)$. بالتأكيد، النتائج الأفضل للمدخلات ستُعرف النموذج الذي يُنتج أكثر التوقعات دقة.
كما تلاحظ شكل النموذج الخطي في المعادلة (1) مشابة بشكل كبير لشكل نموذج متجهات الدعم SVM. الفرق الوحيد في الإشارة. يتشابهة النموذجان بشكل كبير. ولكن، أبعاد الخط العازل في متجهات الدعم SVM يتحكم بإتخاذ القرار: يستخدم للفصل بين مجموعتين. وبهذا، يجب أن يكون أبعد ما يكون بين كل مجموعة والأخرى. في الجانب الآخر، أبعاد الخط العازل في الإنحدار الخطي يتم إختيارة ليكون أقرب ما يكون لكل بيانات التدريب.
يمكنك مشاهدة أهمية النقطة السابقة في الرسم البياني التالي. يُعرض خط الإنحدار (اللون الأزرق الفاتح) للبيانات (النقط الزرقاء) بشكل أحادي الأبعاد. يمكننا إستخدام الخط لتوقع نتائج $y_{new}$ للبيانات الغير مصنفة المدخله $x_{new}$ التي لم تستخدم في بناء النموذج. اذا كان المثال متجهة ذات $D$-الأبعاد، الفارق الوحيد سيكون ان نموذج الإنحدار لن يكون خطاً ولكن سطح مستوي (لمتجة الخواص ثنائية الأبعاد) أو لفائض بعدي $D > 2$.

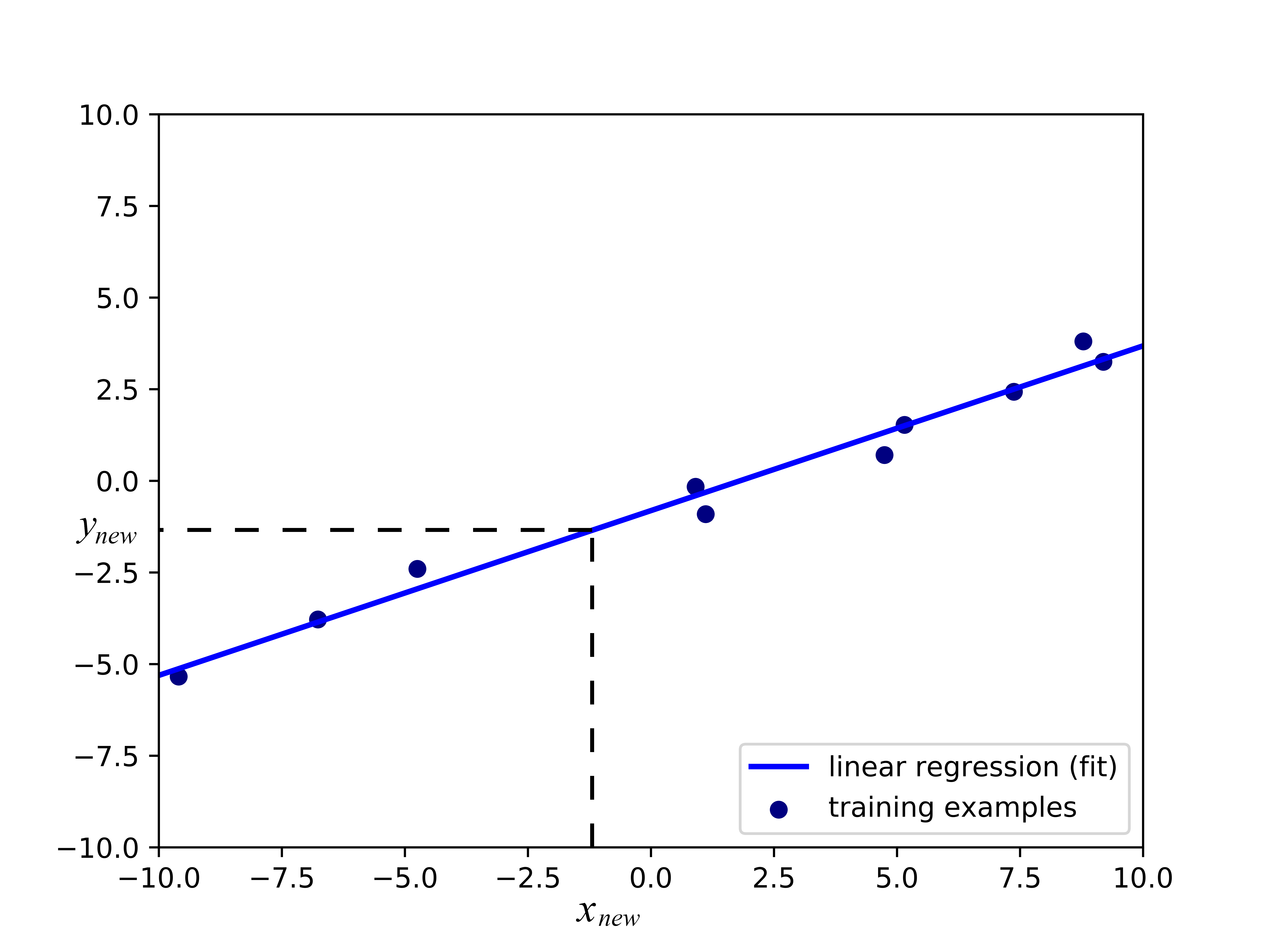صورة 1: إنحدار خطي لمثالث أحادي الأبعاد

يتبين الآن أهمية أن يبقى إنحدار الخط الفاصل أقرب قدر الإمكان إلى بيانات التدريب: إذا كان الخط الازرق بعيد عن النقاط الزرقاء، فأن التوقع $y_{new}$ سيكون غالباً خاطئ.

الحل

لإيجاد الحل المطلوب، خطوة التحسين في الإنحدار الخطي والتي تهدف لإيجاد القيم المثلى لـ $w^*$ و $b^*$ تحاول التقليل من التالي:

$$\displaystyle \min_{w,b} \frac{1}{N} \displaystyle \sum_{i=1...N} (f_{x,b}(x_{i}) - y_{i})^2$$ المعادلة (2)

التعبير $(f(x_{i}) - y_{i})^2$ يطلق عليه دالة الخسارة. تقيس الدالة الأمثلة $i$ التي أخطأت تصنيفها. هذا النوع من دالة الخسارة يطلق عليه دالة الخسارة المربعه Squared Error Loss. جميع الخوارزميات التي تعتمد على النماذج لديها دوال خسارة وما نفعلة لإيجاد النموذج الأفضل هو تقليل متوسط الخسارة ويطلق عليه أيضاً الخطر التجريبي Empirical Risk. متوسط الخسارة للنموذج هو متوسط جميع الأخطاء التي وُجِدت بعد تطبيق النموذج على بيانات التدريب.
لماذا الخسارة في الإنحدار الخطي دالة مُربعه؟ لماذا لا نجد القيمة المطلقة للفرق بين الأهداف الصحيحه $y_{i}$ وقيمة التوقع $f(x_{i})$ وإستخدامها لإيجاد الأخطاء؟ يمكننا ذلك. ويمكننا أيضاً إستخدام التكعيب بدلاً من التربيع.
الآن قد يتضح عدد القرارات التي تبدون عشوائية التي إتخذنائها عند تصميمنا لخوارزمية تعلم الآلة: قررنا إستخدام مزيج من الخصائص الخطية لتوقع النتائج. ولكن يمكن ان نستخدم التربيع او دالة متعددة الحدود لتجميع قيم الخصائص. يمكننا أيضاً إستخدام أي دالة خسارة أخرى نراها مناسبة: الفرق المطلق بين $f(x_{i})$ و $y_{i}$، أو تكعيب الفرق بينهما; الخسارة الثنائية Binary Loss (1 عندما $f(x_{i})$ و $y_{i}$ مختلفين و 0 عندما يكونا متشابهين) قد تكون خيار آخر، صحيح؟

إذا إتخذنا قرارات أخرى لطريقة تشكيل النموذج، طريقة تشكيل دالة الخسارة، وإختيار الخوارزمية التي ستقلل متوسط الخسارة لإيجاد القيم المناسبة للمدخلات، سنكون وقتها قد إخترعنا خوارمزية تعلم آلة مختلفة. يبدو ذلك سهلاً أليس كذلك؟ ولكن لا تستعجل في إختراع خوارزمية جديدة. كونها مختلفة لا يعني أنها ستعمل جيداً في التجارب.

يخترع الأشخاص خوارزميات تعلم جديده لسببين:
- الخوارزمية الجديده تحل مشكلة عمليه أفضل من أي خوارزمية أخرى موجودة.
- الخوارزمية الجديده لديها ضمانات نظرية أفضل عن جودة النموذج التي تنشأة.

المبرر العملي لإختيار نموذج خطي هو سهولته. لماذا نستخدم نموذج مُعقد عندما يمكننا إستخدام السهل؟ سبب آخر هو ان النموذج الخطي نادراً ما يتعرض لفرط التخصيص. فرط التخصيص Overfitting هي خاصية في النموذج تجعلة يتوقع بشكل صحيح جداً للأمثلة المستخدمة وقت التدريب ولكن دائماً ما يخطئ عندما تقدم لهم بيانات ليست موجودة ولم تمر على الخوارزمية في وقت التدريب.

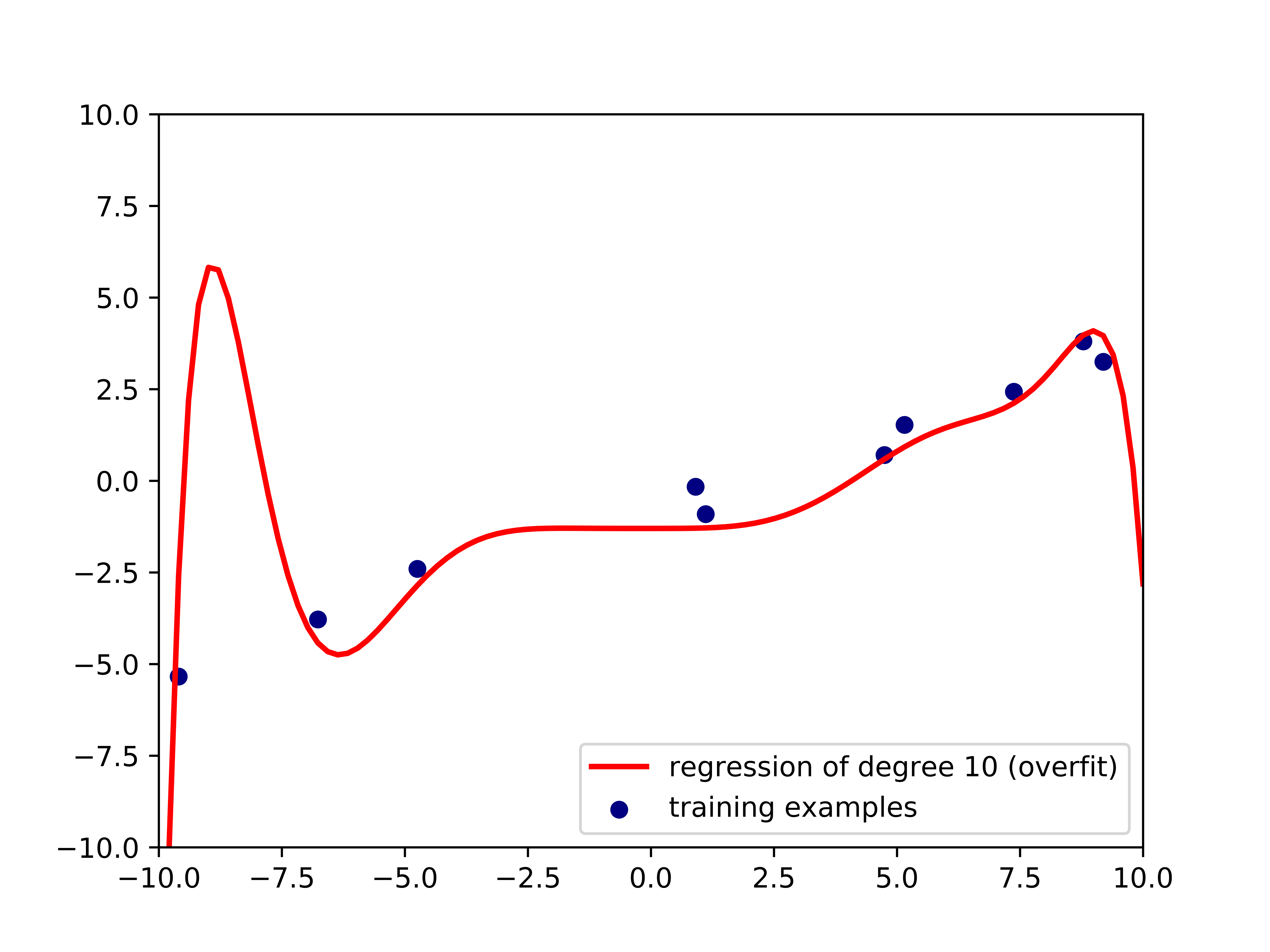صورة 2: فرط التخصيص

يظهر مثال في الصورة 2 عن فرط التخصيص. البيانات التي أستخدمت لبناء خط الإنحدار باللون الأحمر هي نفسها التي أستخدمت في الصورة 1، الفرق الوحيد هنا هي انها إنحدار أحادي Polynomial Regression بدرجة 10. يتوقع الإنحدار بشكل صحيح لكل البيانات المُدربه، ولكن سيفشل بشكل واضح مع بيانات جديده غير مُدرب عليها. سنتكلم أكثر عن فرط التخصيص وكيفية تفادية في الفصل الخامس.
والآن نعرف لماذا الإنحدار الخطي مفيد: لأنه لا يتفرط بالتخصيص بشكل كبير. ولكن ماذا عن الخسارة التربيعية؟ لماذا قررنا أنها ستكون تربيعية؟ في 1705، عالم الرياضيات الفرنسي أدريان ماري ليجاندر، أول من نشر فكرة جمع التربيع لقياس أداء النموذج قال أن تربيع الخطأ قبل جمعة خطوة مناسبة. لماذا قال ذلك؟ القيمة المطلقة غير مناسبة، لأن ليس لديها مشتق مستمر، مما يجعل الداله غير عملية. الدوال الغير عملية تجلب لنا صعوبات عند إستخدام الجبر الخطي لإيجاد أقرب شكل للحل لمشكلة تحسين للنموذج. الشكل الأقرب لإيجاد الدالة الأمثل هي التعبيرات الجبرية البسيطة وغالباً ما يفضل إستخدام طرق التحسين العددية المعقدة، مثل نزول إشتقاقي Gradient Descent.

الأخطاء التربيعية أيضاً مفيدة لأنها تضخم الفرق بين النتائج الصحيحة والتوقعات بناءاً على الفرق. من الممكن أيضاً رفعها إلى 3 أو 4، ولكن مشتقاتها ستكون معقدة للعمل بها.
أخيراً، لماذا نهتم بمشتقة متوسط الخسارة؟ تذكر أن في علم الجبر إذا استطعت إيجاد مشتقة الدالة في المعادلة (2)، يمكننا حينها مساواة الإشتقاق إلى صفر وإيجاد الحل للمعادلات التي ستعطينا القيم الأمثل لـ $w^*$ و $b^*$. يمكنك تجربة ذلك بنفسك بدقائق معدودة.

الإنحدار اللوجستي

أول شئ أقولة عن الإنحدار اللوجستي انه ليس إنحدار، بل خوارزمية تصنيف. الإسم جاء من الإحصاء وذلك بسبب ان العمليات الحسابية للإنحدار اللوجستي مشابهة بشكل كبير لتلك في الإنحدار الخطي.

سنشرح الإنحدار اللوجستي في مثال تصنيف ثنائي. ولكن يمكن إستخدامة لأي حجم من أحجام التصنيف.

مشكلة

في الإنحدار اللوجستي، لا نزال نريد النموذج $y_{i}$ كدالة خطية $x_{i}$، ولكن بـ$y_{i}$ ثنائية لن يكون ذلك سهلاً. المزيج الخطي للخصائص مثل $wx_{i}+b$ هو دالة تمتد من سالف مالا نهاية إلى موجب مالا نهاية، ولكن $y_{i}$ نتيجتها محصوره بقيمتين.

في غياب أجهزة الكمبيوتر، مُجبراً على عمل العمليات الحسابية يدوياً، العلماء في الماضي أرادو إيجاد نموذج تصنيف خطي بأي طريقة. وجدو أنه إذا عرفنا تصنيف سالب بـ0 والموجب بـ1، سنحتاج فقط لإيجاد دالة مستمرة بسيطة مجالها المقابل هو (0،1). في تلك الحالة، إذا كانت النتيجة من النموذج لمدخل $x$ قريبة إلى 0، فأننا نعطية تصنيف سالب لـ$x$، وغير ذلك سيعطى تصنيف موجب. أحدى الدوال القادرة على ذلك هي الدالة اللوجستية البسيطة Standard Logistic Function (وتعرف أيضاً بـ دالة سيجمويد Sigmoid Function).

$$f(x) = \frac{1}{1+e^{-x}}$$

هنا $e$ هي قاعدة اللوغاريثم الطبيعية (تعرف أيضاً بعدد أويلر أو دالة $exp$ في برنامج الإكسل ولغات برمجية أخرى). رسمها البياني كالتالي:

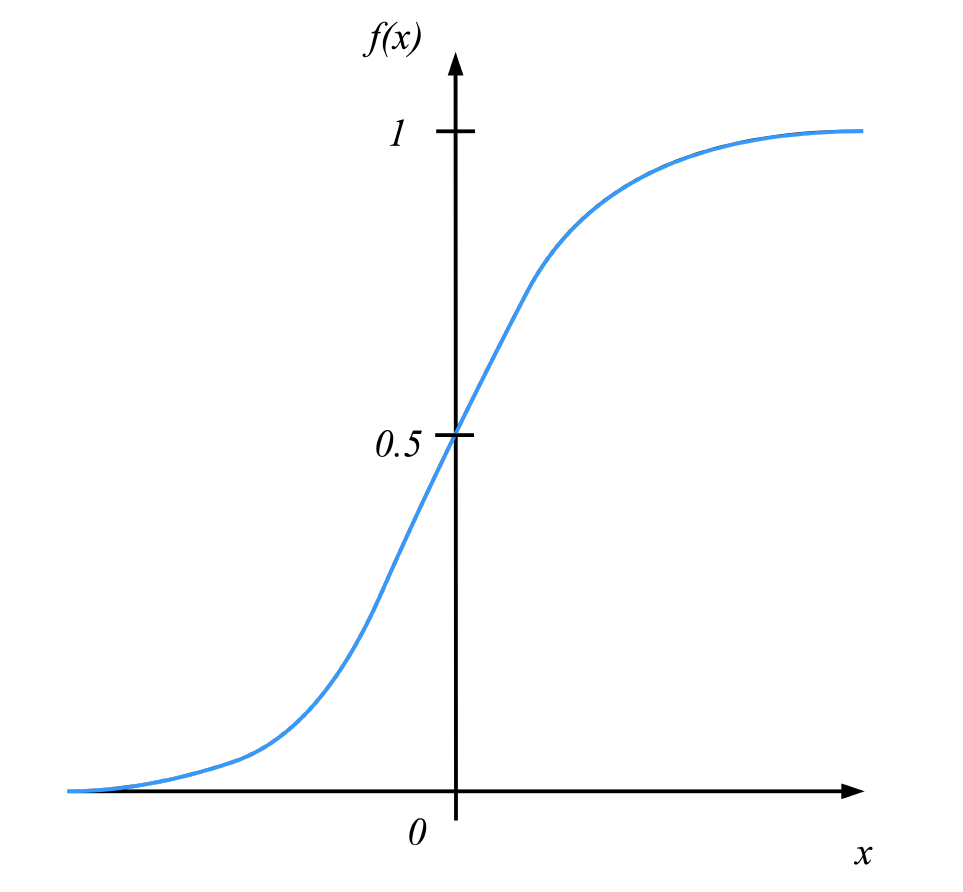صورة 3: دالة لوجستية

بالنظر على الدالة اللوجستية البسيطة في الرسم البياني، نرى كيف أنها مناسبة للتصنيف الذي نرغب به: إذا حسنا القيم $x$ و $b$ بالطريقة الصحيحة، يمكننا قراءة نتائج $f(x)$ أنها إحتمالية ان تكون $y_{i}$ موجبة. على سبيل المثال، إذا كانت أعلى أو مساوية لـ0.5 نقول ان تصنيف $x$ موجب، وغير ذلك سالب. مع التجارب، إختيار قيمة الفصل، 0.5، يمكن أن يتغير حسب المشكلة. سنعود لذلك في الفصل الخامس عنما نتحدث عن تقيم أداء النموذج. إذاً، معادلة نموذج الإنحدار اللوجستي ستبدو كالتالي:

$$f_{w,b}(x) = \frac{1}{1+e^{-(wx+b)}}$$ المعادلة (3)

يمكن رؤية $wx+b$ التي سبق ان رأيناها في الإنحدار الخطي. الآن، كيف نجد القيم النموذج المناسبة لـ $w^*$ و $b^*$؟ في الإنحدار الخطي، نقوم بتقليل الخطر التجريبي والذي عُرف بمتوسط دالة الخسارة.

الحل

في الإنحدار اللوجستي، بدلاً من إستخدام الخسارة التربيعية ومحاولة إيجاد التقليل من الخطر التجريبي، نحاول تكبير دالة الإحتمالية Likelihood Function، دالة الإحتمالية في الإحصاء توجد لنا إحتمالية ظهور النتائج بناءاً على النموذج.

على سبيل المثال، ليكن لدينا أمثلة مصنفة $(x_{i},y_{i})$ في بيانات التدريب. لنقل أيضاً أننا وجدنا (توقعنا) بعض القيم $\hat{x}$ و $\hat{b}$ من مدخلاتنا. إذا قمنا بتجربة النموذج $f_{\hat{x},\hat{b}}$ على $x_{i}$ بإستخدام المعادلة (3) سينتج لنا قيمة $0 < p < 1$. إذا كانت $y_{i}$ موجبة، إحتمالية ان تكون $y_{i}$ موجبة بناءاً على نموذجنا، معطاة من القيمة $p$. بنفس النهج، أذا كانت $y_{i}$ سالبة، إحتمالية ان تكون سالبة $1-p$.

معيار التحسين في الإنحدار اللوجستي يسمى الإحتمالية الكبرى Maximum Likelihood. بدلاً من تقليل متوسط الخسارة، كما في الإنحدار الخطي، الآن نزيد من الإحتمالية في بيانات التدريب بنموذجنا:

$$\displaystyle \max_{w,b} L_{w,b}$$

وفيه

$$L_{w,b} = \displaystyle \prod_{i= 1...N} f_{w,b}(x)^{y_{i}}(1-f_{w,b}(x))^{i-y_{i}}$$ المعادلة (4)

و $f_{w,b}(x)^{y_{i}}(1-f_{w,b}(x))^{i-y_{i}}$ هي عملية رياضية تعني “ $f_{w,b}(x)$ عندما $y_{i} = 1$ و $(1-f_{w,b}(x))$ عندما تكون غير ذلك”.
قد تلاحظ اننا استخدمنا علامة الضرب $\prod$ في الدالة بدلاً من علامة الجمع $\sum$ والتي أستُخدمت في الإنحدار الخطي. ذلك لأن إحتمالية التصنيف $N$ للأمثلة $N$ هي نتيجة ضرب الإحتمالية في كل القيم (بفرض أن كل القيم مستقلة عن بعضها البعض). يمكن موازات ذلك مع حاصل ضرب نتائج الإحتمالات في مصفوفة من الإختبارات المستقلة في نظرية الإحتمالات.
بسبب دالة $exp$ المستخدمة في النموذج، عملياً، من الأفضل تكبير لوغارثمية الإحتمال بدلاً من الإحتمال. لوغارثمية الإحتمال تعرف كالتالي:

$$LogL_{w,b} = ln(L(_{w,b}(x))=\displaystyle \sum_{i= 1...N}^Ny_{i} ln f_{w,b}(x) + (1-y_{i})ln(1-f_{w,b}(x))$$

الحل لمشكلة التحسين الجديده سيكون مشابه للأصلية لأن الوغارثم هي دالة متخصصه بالزيادة. الجزء الأخير يعني حينما نقوم بزيادة اللوغاريثم لأحدى الدوال، فأننا نزيد الدالة نفسها أيضاً.
على عكس ذلك في الإنحدار الخطي، لا يوجد حل لمشكلة التحسين السابقة. إحدى الإجراءات التحسينية الشائعة في تلك الحالات هو النزول الإشتقاقي. سنتحدث عنه في الفصل القادم.

تعلم شجرة القرار

شجرة القرار هي رسم بياني دوري يستخدم لإتخاذ القرارات. في كل فرع من الرسم البياني، خاصية معين $j$ من متجهة الخواص يتم فحصها. إذا كانت القيمة أقل من قيمة الفصل، فإنها تتجهة للفرع الأيسر، وعكس ذلك، ستتجه للفرع الأيمن. عند الوصول إلى آخر فرع في الشجرة، يتم إتخاذ القرار على المثال المدخل.

كما هو مذكور في عنوان الجزء الحالي، تتعلم شجلة القرار من البيانات المدخلة لها.

مشكلة

كما في السابق، لدينا مجموعة من البيانات المُصنفة; التصنيف على شكل مصفوفة {0,1}. نريد بناء شجرة قرار تمكنا من توقع تصنيف القيمة المعطاة.

الحل

توجد الكثير من الأشكال لدالة لخوارزمية شجرة القرار. في هذا الكتاب، سنستخدم واحدة فقط، يطلق عليها ID3. معيار التحسين في هذه الحالة هو متوسط لوغارثمية الإحتمال:

$$\displaystyle \frac{1}{N}=\displaystyle \sum_{i= 1}^Ny_{i} ln f_{ID3}(x) + (1-y_{i})ln(1-f_{ID3}(x))$$ المعادلة (5)

هنا $f_{ID3}$ هي شجرة القرار.
حتى الآن، تبدو الدالة مشابهه بشكل كبير للإنحدار اللوجستي. ولكن عكس ذلك، خوارزمية التعلم في الإنحدار الخطي تبني نموذج محدود Parametric Model $f_{w*,b*}$ عن طريق البحث عن الحل المثالي لمعيار التحسين، خوارزمية ID3 تحسن بشكل تقريبي عن طريق بناء نموذج غير محدود Non-parametric Model $f_{ID3}(x)=Pr(y_i=1|x)$.

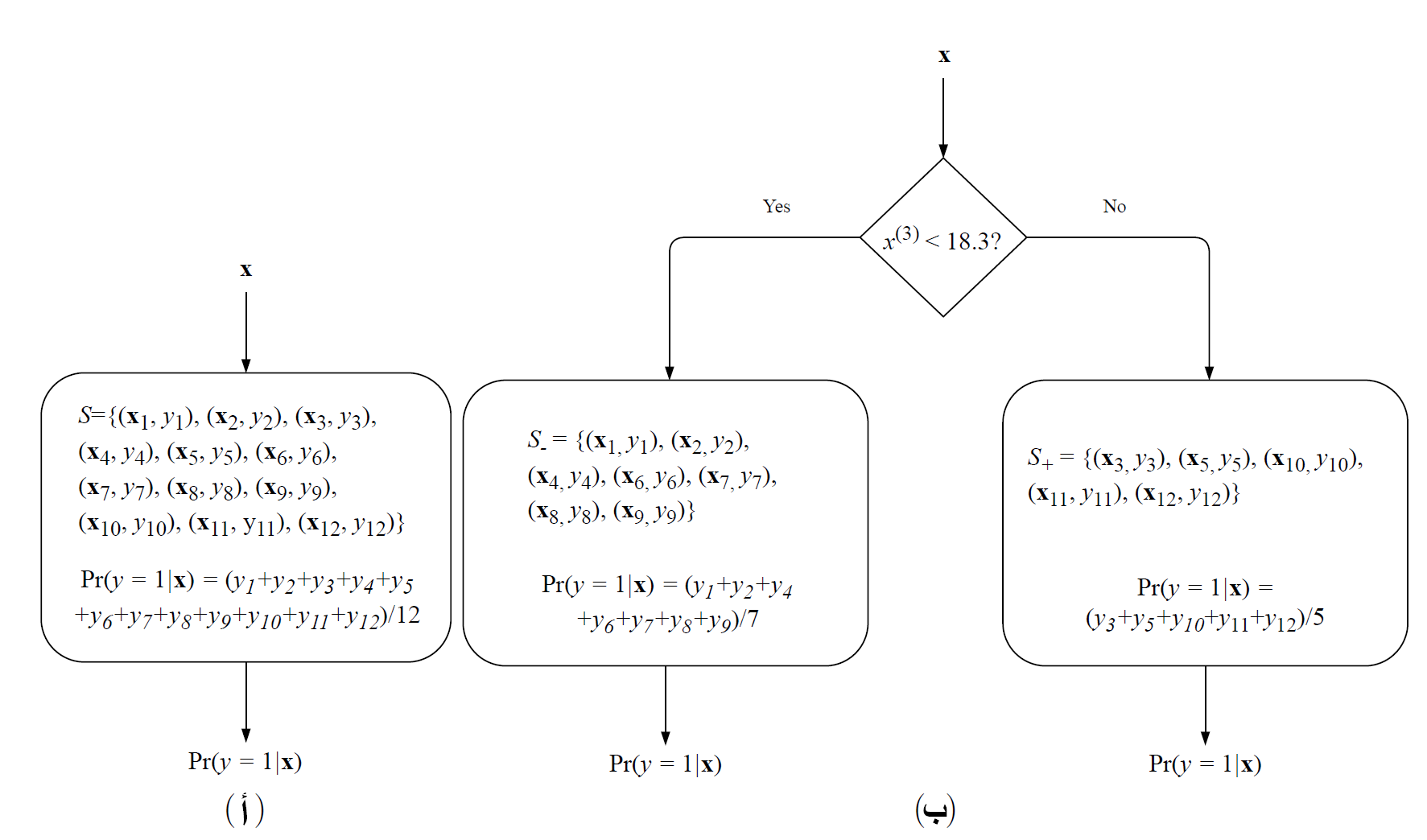صورة 4: رسم بياني لخوارزمية شجرة القرار. المجموعة S تحتوي على 12 مثال مُصنف. الجزء (أ) في البداية، تحتوي فيه الشجرة على الفرع الأول فقط; وتتوقع نفس التوقع لجميع المدخلات. في الجزء (ب) شجرة القرار بعد أول عملية فصل; تختبر ما إذا كان الخاصية 3 أقل من 18.3، وبناءاً على النتيجة، يتم التوقع بإحدى الفرعين.

خوارزمية التعلم ID3 تعمل كالتالي. لنجعل S مصفوفة لبيانات مُصنفة. في البداية، شجرة القرار لديها فرع واحد يحتوي على كامل البيانات: $S={(x_i,y_i)}_{i=1}^{N}$. تبدأ بنموذج ثابت تماماً $f_{ID3}^{S}$:

$$f_{ID3}^{S}\displaystyle \frac{1}{|S|}=\displaystyle \sum_{(x,y) \in S}y$$ المعادلة (6)

فيه $|S|$ تعني حجم المصفوفة S. التوقع من النموذج بالأعلى، $f_{ID3}^{S}(x)$، سيكون نفسه لأي من المدخلات x. الرسم البياني لشجرة القرار المعنية هي الجزء (أ) في الصورة 4. ثم نبحث بجميع الخصائص $j=1 ... D$ وجميع قيم الفصل $t$، ونقوم بفصل المصفوفة $S$ إلى قسمين: $S_-={(x,y)|(x,y) \in S, x^{(j)}<t}$ و $S_+={(x,y)|(x,y) \in S, x^{(j)} \ge t}$.
المصفوفتين الجديدتين ستكون فرعين للشجرة، ونقيمها، لجميع الازواج المحتملة (j,t) وما إذا كان الفصل مناسب مع $S_-$ و $S_+$. أخيراً، نختار النتيجة الأفضل (j,t)، ونفصل $S$ إلى $S_-$ و $S_+$، لتكون فرعين جديدين، ونستمر بتكرار ذلك على $S_-$ و $S_+$ (أو التوقف إذا كان الفصل لا يكون نموذج أفضل). شجرة القرار بعد عملية فصل واحدة هي (ب) في الصورة 4.
والآن قد تتسائل عن ما تعنية الجملة “تقييم جودة التقسيم”. في ID3، مدى جودة التقسييم تقاس بإستخدام Entropy الإنتروبيا. الإنتروبيا لمصفوفة S:

$$H(S) = -f_{ID3}^{S}\log f_{ID3}^{S}-(1-f_{ID3}^{S})\log (1-f_{ID3}^{S})$$

عندما نقسم المصفوفة بناءاً على معيار معين j وقيمة فصل t، الإنتروبيا للفصل، $H(S_-,S_+)$، هي ببساطة مجموع النتائج الموزونه للإنتربيا:

$$H(S_-,S_+)=\displaystyle \frac{|S_-|}{|S|}H(S_-)+\displaystyle \frac{|S_+|}{|S|}H(S_+)$$ المعادلة (7)

إذاً، في ID3، في كل خطوة، وفي كل فرع، نوجد قيمة فصل تقلل الإنتروبيا بواسطة المعادلة 7 أو نتوقف في ذلك الفرع.
تتوقف الخوارزمية في فرع معين لأي من الأسباب التالية:

جميع الأمثلة في الفرع مصنفة بشكل صحيح بواسطة نموذج النتيجة الواحده (المعادلة 7).
لم نستطع إيجاد قيمة/صفة للفصل عليها.
الفصل يقلل الإنتروبيا إلى أقل من $\epsilon$ (القيمة التي يجب إيجادها عن طريق التجارب),
الشجرة وصلت إلى الحد الأعلى من العمق $d$ (أيضاً يجب إيجادها عن طريق التجارب).

لأن في ID3، القرار لفصل البيانات في كل عملية تكرار يتم مسبقاً (لا يعتمد على الفصل المستقبلي)، الخوارزمية لا تضمن الحل الأمثل. يمكن تحسين النموذج عن طريق بعض الأساليب مثل التراجع Backtracking عند البحث عن شجرة القرار الأمثل على حساب أخذ وقت أطول لبناء النموذج.

الفصل بناءاً على الإنتروبيا يعتبر منطقي: الإنتروبيا تصل إلى أقلها وهو 0 عندما تكون جميع الأمثل في $S$ تحمل نفس التصنيف; وفي الجانب الآخر، الإنتروبيا تصل أعلاها وهو 1 عندما يكون نصف الأمثلة في $S$ مصنفة بـ1، ويجعل ذلك ذلك الفرع غير مفيد في التصنيف. السؤال الباقي هو كيف يمكن لهذه الخوارزمية الوصول للحد الأقصى لمتوسط لوغارثمية الإحتمال. سنجيب عن ذلك لاحقاً.

آلة المتجهات الداعمة SVM

تحدثنا ببساطة عن SVM في المقدمة، لذا هذا الجزء سيملئ بعض الفراغات فقط. هناك سؤالين مهمين يجب علينا إجابتهم:

ما الحل إذا كان هناك ضوضاء وبيانات غير مرغوب فيها ولا يوجد خط فاصل يفصل البيانات الموجبة عن السالبة بشكل مناسب؟
إذا لم نستطع فصل البيانات بخط فاصل، ولكن يمكن فصلها بدالة متعددة الحدود أعلى؟

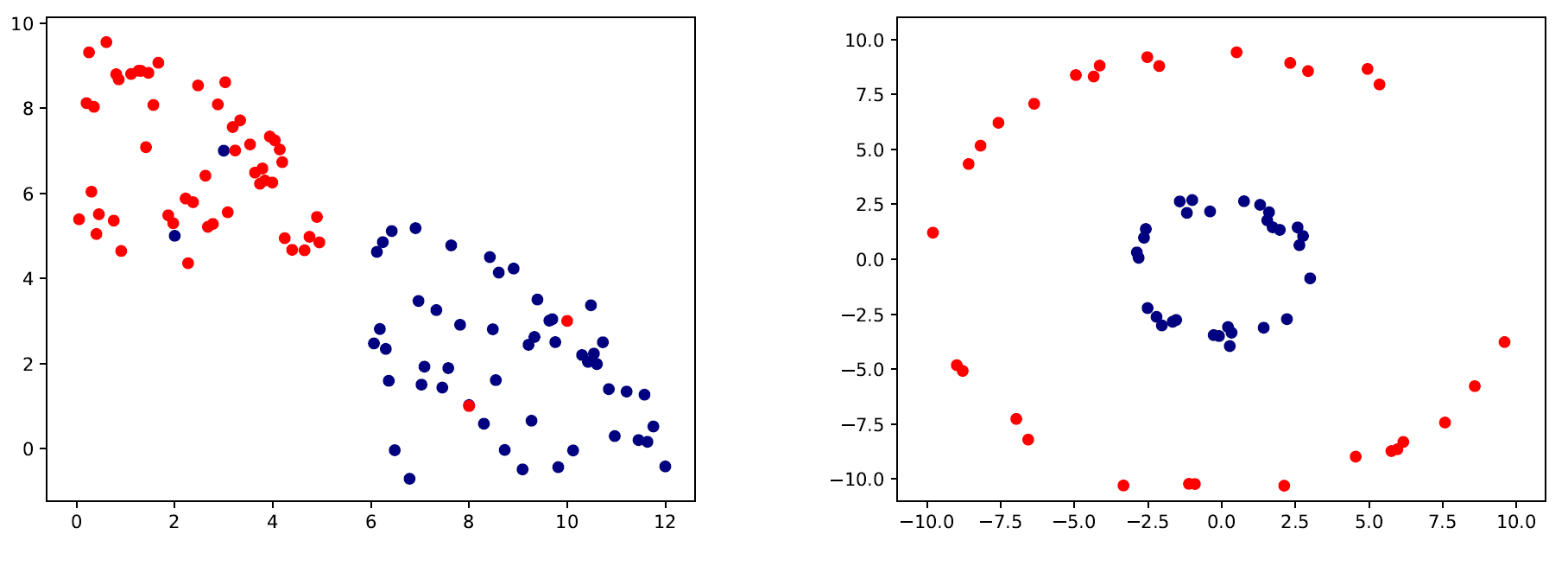صورة 5: حالات يصعب الفصل الخطي فيها. اليسار: وجود الضوضاء. اليمين: غير الخطية.

يمكنك مشاهدة ان في كلا المثالين في الصورة 5، في الصورة على اليسار، يمكن فصل البيانات بخط مستقيم لولا وجود البيانات غير المرغوب فيها (الشواذ أو بيانات مصنفة بشكل خاطئ). في اللصورة على اليمين، خط حد القرار على شكل دائرة وليس خط مستقيم.
تذكر أن في SVM، نريد أن نوفي الشروط التالية:
أ- $wx_i -b \ge 1$ إذا $y_i=+1$ ب- $wx_i -b \le 1$ إذا $y_i=-1$

نريد أيضاً التقليل من $w$ ليكون الخط الفاصل بعيد بنفس البعد عن أقرب قيمة من كل فئة من النتائج. التقليل من $w$ مساوي للتقليل من $\frac{1}{2}\|w\|^2$ وإستخدام هذا المصطلح يجعل من الممكن تطبيق تحسين برمجي تربيعي لاحقاً. إذاً مشكلة التحسين في SVM تبدو كالتالي:

$$\min \frac{1}{2}\|w\|^2 s.t. y_i(x_iw+b)-1 \ge0, i=1...N$$ المعادلة (8)

التعامل مع الضوضاء

لتوسيع SVM للحالات التي لا يمكن فصل البيانات فيها خطياً، نستخدم Hinge loss function دالة الخسارة المفصلية:

$$\max(0,1 -y_i(wx_i-b))$$

دالة الخسارة المفصلية تساوي صفر إذا كان الشرطين أ و ب صحيحين، بمعنى أصح، اذا كانت $wx_i$ تقع في الجانب الصحيح من خط القرار. للبيانات في الجانب الخطأ من خط القرار، قيمة الدالة تتناسب مع المسافه من بين القيمة وخط القرار. ونحن حينها نريد أن نقللها

$$C\|w\|^2+\frac{1}{N} \displaystyle \sum_{i= 1}^N \max(0,1-y_i(wx_i-b))$$

فيها المتغير $C$ يقرر قيمة التنازل بين زيادة حجم خط القرار وضمان أن كل $x_i$ تقع في الجانب الصحيح من خط القرار. يتم إختيار قيمة $C$ عادة مع التجارب، كما في خوارزمية ID3 ومتغيراتها $\epsilon$ و $d$. آليات المتجهات الداعمة التي تُحسن بدالة بالخسارة المفصلية يطلق عليها SVM ذات الهوامش اللينة، بينما الدالة الرئيسية يطلق عليها SVM ذات الهوامش القوية.
كما ترى، للقيم العالية من $C$، الشرط الثاني من دالة الخسارة سيكون غير مهم، لذا ستحاول خوارزمية آلة المتجهات الداعمة إيجاد أعلى هامش بواسطة تجاهل التصنيف الخاطئ. حين نقلل قيمة $C$، ستزيد علينا تكلفة التصنيفات الخاطئة، لذا تحاول الخوارزمية تقليل الأخطاء عن طريق التضحية بحجم الهامش. كما تحدثنا مسبقاً، زيادة الهامش افضل للتعميم. لذا، $C$ تقوم بتنظيم التفضيل بين تصنيف بيانات التدريب شكل صحيح (تقليل الخطر التجريبي) وتصنيف البيانات المستقبلية بشكل صحيح (التعميم).

التعامل مع الغير خطية

يمكن لآلة المتجهات الداعمة التأقلم والعمل مع البيانات التي لا يمكن أن تفصل بخط فاصل في فضاءها الطبيعي. ولكن إذا أستطعنا أن نحول الفضاء الطبيعي لها إلى فضاء ذو أبعاد أعلى، نأمل بأن تكون الأمثلة تقبل الفصل خطياً بعد التحويل إلى هذا الفضاء عالي الأبعاد. في SVM، إستخدام دالة لتحولي الفضاء الطبيعي إلى فضاء عالي الأبعاد بشكل كامل خلال عملية تحسين دالة الخسارة يطلق عليها Kernel trick حيلة النواة.
يمكن مشاهدة شكل تأثير إستخدام حيلة النواة في الصورة 6. كما ترى، يمكن تحويل بيانات ثنائية الأبعاد لا يمكن فصلها بخط فاصل إلى بيانات ثلاثية الأبعاد يمكن فصلها بإستخدام طريقة معينة: $\phi:\mathbf{x}\rightarrow\phi(\mathbf{x})$ فيها $\phi(\mathbf{x})$ هي مصفوفة ذات ابعاد اعلى من $\mathbf{x}$. على سبيل المثال، الرسم ثنائي الأبعاد (يسار) في الصورة 6، طريقة الرسم $\phi$ للمثال $\mathbf{x}=[q,p]$ التي تحول المثال إلى فضاء ثلاثي الأبعاد (يمين) ستبدو كالتالي: $\phi([q,p])=(q^2,\sqrt{2qp},p^2)$ ، فيه $q^2$ تعني $q$ تربيع. يمكن أن نرى أن البيانات يمكن فصلها خطياً الآن.
ولكن، لا يمكن أن نعرف مسبقاً أن كانت طريقة $\phi$ ستعمل على بياناتنا. إذا بدأنا أولاً بتحويل جميع المدخلات بإستخدام طريقة الرسم إلى مصفوفات ذات أبعاد أعلى وطبقنا SVM على البيانات، إن جربنا كل دوال الرسم الممكنه، ستكون العملية غير فعالة ولن نجد حلاً لمشكلة التصنيف لدينا.

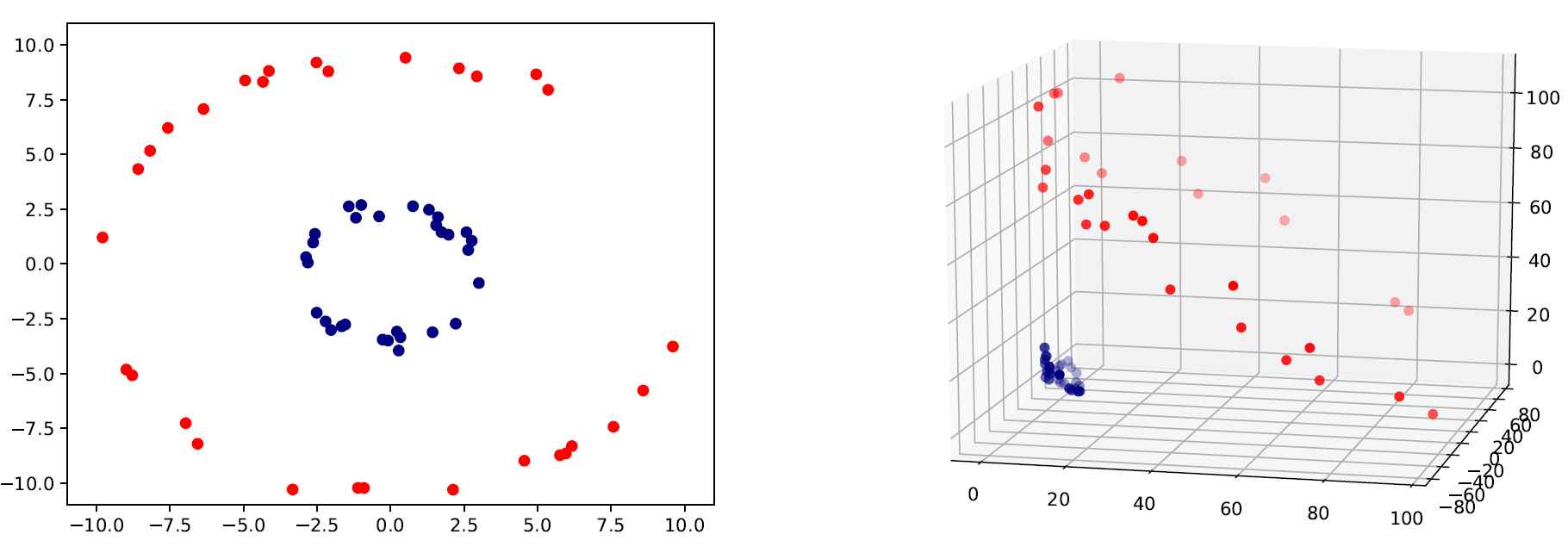آلة المتجهات الداعمة ثنائية وثلاثية الأبعاد

صورة 6: اليسار: الرسمه الأصلية ثنائية الأبعاد التي لا يمكن فصلها خطياً. اليمين: نفس البيانات يمكن فصلها بعد تحويلها لفضاء ثلاثي الأبعاد.

لحسن الحظ، العلماء أكتشفو طريقة لإستخدام دوال النواة ( أو ببساطة النواة) للعمل بشكل سهل مع الفضاءات عالية الأبعاد إثناء عمل نموذج SVM بدون القيام بعملية التحويل. لمعرفة كيفية عمل دوال النواة، يجب علينا أولاً عرض كيفية عمل خوارزمية التحسين لآلة المتجهات الداعمة لإيجاد القيم المناسبة لكل من $\|w\|$ و $b$.
الطريقة التي تستخدم لعملية التحسين في المعادلة 8 هي طريقة مضاعفات لاغرانج. بدلاً من حل المشكلة الأساسية في المعادلة 8، من الأفضل حل مشكلة مشابهه تبدو كالتالي:

$$\displaystyle\max_{a_1...a_N}\displaystyle \sum_{i= 1}^N a_i-\frac{1}{2}\displaystyle \sum_{i= 1}^N\displaystyle \sum_{k= 1}^Ny_ia_i(\mathbf{x}_i\mathbf{x}_k)y_ka_k$$ تخضع إلى $$\displaystyle \sum_{i= 1}^Na_iy_i=0 و a_i\ge0, i=1 ...N$$

وفيه $a_i$ هي مضاعفات لاغرانج. بهذه الطريقة، مشكلة التحسين تصبح مشكلة تحسين تربيعية محدبة، يمكن حلها بكفاءة عن طريق خوارزميات التربيع. الآن، ربما قد لاحظت في المعادلة العلوية، هناك مصطلح $\mathbf{x}_i\mathbf{x}_k$، وهنا هو المكان الوحيد الذي يستخدم فيه مصفوفة الخصائص. إذا اردنا ان نغير فضاء المصفوفة إلى فضاء أعلى، نحتاج لتغير $\mathbf{x}_i$ إلى $\phi(\mathbf{x}_i)$ و $\mathbf{x}_j$ إلى $\phi(\mathbf{x}_j)$ ثم ضرب كل من $\phi(\mathbf{x}_i)$ و $\phi(\mathbf{x}_j)$. سيكون فعل ذلك مكلفاً جداً.
على الجانب الآخر، نحن مهتمون بنتيجة عملية الضرب فقط، وهو رقم صحيح. لا نهتم بكيفية حصولنا على هذا الرقم ما دام الرقم صحيح. بإستخدام حيلة النواة يمكننا التخلص من تكلفة التغير لمصفوفة الخصائص الأصلية إلى مصفوفة ذات أبعاد أعلى وتجنب حساب نتيجة الضرب النقطي لهم. نُبدل ذلك بعملية بسيطة على مصفوفة الخصائص الأصلية التي تعطي نفس النتائج. على سبيل المثال، بدلاً من تحويل $(q_1,p_1)$ إلى $(q_1^2,\sqrt{2q_1p_1},p_1^2)$ و $(q_2,p_2)$ إلى $(q_2^2,\sqrt{2q_2p_2},p_2^2)$ وثم إيجاد نتيجة الضرب النقطي لـ $(q_1^2,\sqrt{2q_1p_1},p_1^2)$ و $(q_2^2,\sqrt{2q_2p_2},p_2^2)$ للحصول على $(q_1^2q_2^2+2q_1q_2p_1p_2+p_1^2p_2^2)$ يمكننا إيجاد نتيجة الضرب النقطي بين $(q_1,p_1)$ و $(q_2,p_2)$ لإيجاد $(q_1q_2+p_1p_2)$ ثم تربيعها للحصول على نفس النتيجة لـ $(q_1^2q_2^2+2q_1q_2p_1p_2+p_1^2p_2^2)$.
هذا كان مثال لحيلة النواة واستخدمنا النواة التربيعية $k(\mathbf{x}_i,\mathbf{x}_k)=(\mathbf{x}_i\mathbf{x}_k)^2$.
يوجد عدد أكثر من دوال النواة، الأكثر إستخداماً هي RBF نواة:

$$k(\mathbf{x}, \mathbf{x'})=\exp\displaystyle \left(-\frac{\|\mathbf{x}- \mathbf{x'}\|^2}{2\sigma^2}\right)$$

وفيه $\|\mathbf{x}- \mathbf{x'}\|^2$ هي Euclidean distance المسافة الإقليدية التربيعية بين مصفوفتين من الخصائص. المسافة الإقليدية ممثلة بالمعادلة التاليه:

$$d(\mathbf{x}_i, \mathbf{x}_k)={\sqrt {\left(x_i^{(1)}-x_k^{(1)}\right)^2+\left(x_i^{(2)}-x_k^{(2)}\right)^2+\cdots +\left(x_i^{(N)}-x_k^{(N)}\right)^2}} =\sqrt {\displaystyle \sum_{j= 1}^D \left(x_i^{(j)}-x_k^{(j)}\right)^2}$$

يمكن ملاحظة ان فضاء الخصائص لنواة RBF غير محدودة الأبعاد. بتغير المتغير $\sigma$، محلل البيانات يمكن أن يختار بين الحصول على خطوط قرار سلسة أو منحنية في الفضاء الأصلي.

خورازمية أقرب الجيران KNN

خوارزمية أقرب الجيران KNN هي خوارزمية غير حدودية. على عكس باقي الخوارزميات التي تتجاهل بيانات التدريب بعد بناء النموذج، الخوارزمية تبقي جميع بيانات التدريب في ذاكرتها. عندما تأتي قيمة جديدة، قيمة لم ترها من قبل، تقوم الخوارزمية بإيجاد $k$ الأقرب إلى المثال في الفضاء متعدد الأبعاد $D$ وتعيد أكثر التصنيفات تكراراً (في حال كانت المشكلة تصنيفية) أو المتوسط (إذا كانت المشكلة خطية).

قرب أقرب نقطتين تحدد بواسطة دالة خاصة للبُعد. على سبيل المثال، المسافة الإقليدية التي سبق ذكرها تستخدم غالباً في التدريب. إقتراح آخر لقياس البُعد Cosine Similarity جيب التماثل السلبي. جيب التماثل مُعرف كالتالي:

$$\cos(\mathbf{x}_i, \mathbf{x}_k)= \frac{\sum_{j= 1}^D x_{i}^{(j)}x_{k}^{(j)}}{\sqrt{\sum_{j= 1}^D\left(x_i^{(j)}\right)^2} \sqrt{\sum_{j= 1}^D\left(x_k^{(j)}\right)^2}}$$

هي مقياس لمدى تشابة الإتجاهات لمصفوفتين. إذا كانت الزاوية بين مصفوفتين تساوي 0 درجة، إذا كلا المصفوفتين تتجهان إلى نفس الطريق وجيب التماثل يساوي 1. اذا كانت المصوفتين متعامدتان، فأن جيب التماثل تساوي 0. للمصفوفات التي تشيران إلى عكس الإتجاه، جيب التماثل يكون فيها مساوي -1. إذا أردنا إستخدام جيب التماثل كمقياس للمسافه، فيجب علينا ضربة في -1. مقياسات أخرى شهيره لقياس المسافه هي مقياس تشيبيشيف، ماهالانوبيس، هامينق لقياس المسافة. إختيار مقياس المسافه، وكذلك قيمة $k$، يتحكم ويقررها المحلل قبل تشغيل الخوارزمية. إذاً هي متغيرات. مقياس المسافة يمكن تعلمه أيضاً من البيانات (وأيضاً يمكن توقعه). سنتحدث عن مزيد من ذلك في اجزاء لاحقة.
الآن تعلمنا كيف نبني خوارزمية النموذج وكيف تتم عملية التوقع. أحد الأسئلة المهمة هنا هو ما عمل دالة الخسارة؟ بدون غرابة، لم يتم دراسة اجابته في الكتب، رغم شهرة الخوارمزية منذ بداية الستينات. المحاولة الوحيدة لتحليل دالة الخسارة لخوارزمية KNN كان بواسطة لي و يانق في 2003.
للتبسيط، فإننا نوجد أستنتاجاتنا تحت أفتراضات التصنيف الثنائي ($y\in$ {0,1}) مع جيب التماثل وتسوية Normalized خصائص المصفوفة. بهذه الإفتراضات، KNN تقوم بعملية تصنيف خطي مع مُعامل المصفوفة.

$$\mathbf{w}_\mathbf{x}=\displaystyle\sum_{(\mathbf{x'},\mathbf{y'})\in R_k(\mathbf{x})}\mathbf{x'}\mathbf{y'}$$ المعادلة (9)

فيها $R_k(\mathbf{x})$ هي مصفوفة $k$ لأقرب الجيران للقيمة المدخلة $\mathbf{x}$. المعادلة العلوية تقول ان نأخذ مجموع كل قيم أقرب الجيران لأحد القيم المدخله $\mathbf{x}$ عن طريق تجاهل تلك القيم المساوية لصفر. قرار التصنيف هنا يأخذ عن طريق تعريف قيمة فصل من الضرب النقطي $\mathbf{w}_\mathbf{x}\mathbf{x}$ والذي، في حالة تسوية خصائص المصفوفات، مساوي لجيب التماثل بين $\mathbf{w}_\mathbf{x}$ و $\mathbf{x}$.
الآن، يتم تعريف دالة الخسارة كالتالي:

$$L=-\displaystyle\sum_{(\mathbf{x'},\mathbf{y'})\in R_k(\mathbf{x})}\mathbf{x'}\mathbf{y'}\mathbf{w}_\mathbf{x}+\frac{1}{2}\|\mathbf{w}\|^2$$

وجعل مشتقة الدرجة الأولى في الجانب الأيمن تساوي صفر يوجد لنا معامل المصفوفة في المعادلة رقم 9.

تم ترجمة هذا الجزء قبل إعلان المؤلف أن الكتاب تُرجم وسيتم نشرة للعربية من أحدى الجهات في دولة الإمارات.

شكراً لكل من عبدالعزيز الطويان و نهى الغامدي على تعاونهم في التدقيق والتصحيح والترجمة.

كُتب في 25/10/2019