📊 الإنحياز والتباين

الإنحياز والتباين أحد أهم المصطلحات في النمذجة الإحصائية، كذلك في تعلم الآلة. ولكن فهم هذه المصطلحات في مجتمعات تعلم الآلة غير واضح جداً، ذلك لأن كثير من المقالات تحاول التقليص من مفهومها “ الإنحياز = فرط التعميم، التباين = فرط التخصيص، أو بعرض الرسم البياني “ . هذه المصطلحات مناسبة عند الحاجة لوصف أداء نموذج بشكل سريع “هذا النموذج لدية إنحياز مرتفع وتباين منخفض“، أرى أن هذه المقالات تخفي المقايضة التي لا تظهر بين الانحياز والتباين. اتمنى أن يوضح هذا المقال للقارئ توضيحاً أكثر للإنحياز والتباين في النماذج الإحصائية.

النمذجة الإحصائية

ظهر الإنحياز والتباين من مجال النمذجة الإحصائية. النمذجة الإحصائية هو المجال الذي يحاول وضع نموذج في بيانات مُجَمعة لهدف:

التنبؤ.
الفهم.

مثال: بيانات منازل بوستن الشهيرة هي بيانات تم جمعها بواسطة خدمة التعداد السكاني في الولايات المتحدة في عام 1996. تحتوي على عدة متغيرات مثل: معدل الجريمة للفرد، عدد الغرف لكل مسكن، نسبة الشركات غير شركات التجزئة، والسعر.

إذا أردنا بناء نموذج لسعر المنازل، سنضع كل المتغيرات الأخرى كمتغيرات للنموذج وسعر المنزل هو المخرج الذي سيتم توقعه. إذا كان لدينا $p$ كعدد المتغيرات $X_{1},X_{2}, \ldots , X_{p}$ والمخرج هو $Y$، فيمكننا الإفتراض أن نموذج $Y$ بإستخدام $X$ يمكن تعريفة كالتالي:

$$Y= f(X_{1},X_{2}, \ldots , X_{p}) + \epsilon $$

في هذه المعادلة، لاحظ أن الدالة $f(X)$ ثابتة، أيضاً هناك $\epsilon$ في المعادلة. هذة الإشارة تعني الخطأ. وهو الفرق بين القيمه التي توقعها النموذج والقيمه الحقيقه ويمكن أن يمثل اشياءً أخرى مثل الضوضاء و العشوائية. المهم هنا هو أن $\epsilon$ لا تعتمد على $X$ ولديها متوسط يساوي صفر.

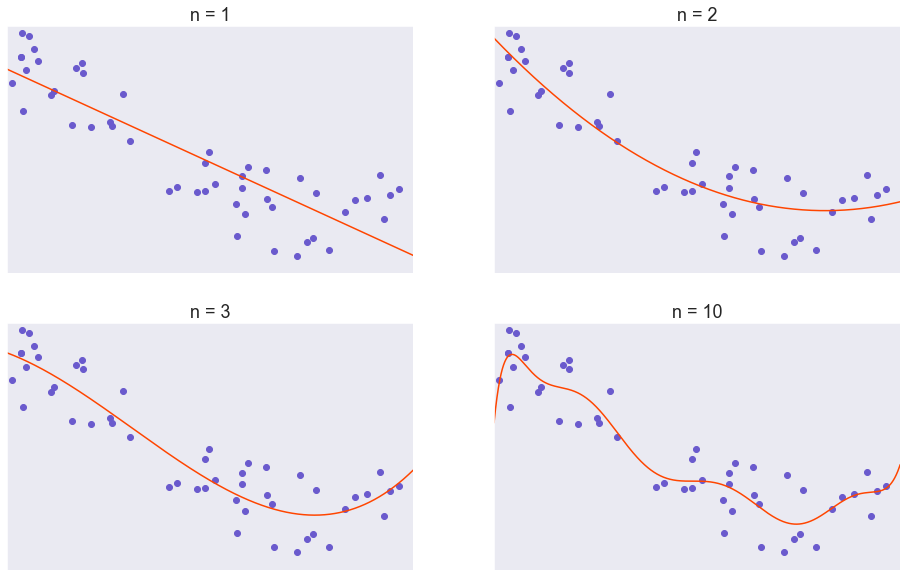
إذا أردنا البدء ببناء نموذج لهذة البيانات، لن نستطيع الوصول لجميع نقاط البيانات لدينا كونها لا تمثل كامل المجتمع (جميع نقاط البيانات يمكن تسميتها “المجتمع”). ولكن، لدينا فقط عينة محدودة من نقاط البيانات (تسمى “عينة”). هنا، لدينا عينة من 50 نقطة.

لضبط النموذج على البيانات، من الأفضل البدء بشكل بسيط، ثم الإنتقال للمسائل المعقدة. هنا إستخدمنا نموذج متعددة الحدود فيه $n$ هي أعلى قوة، البداية من $n=1$ (انحدار خطي) ثم الزيادة في قيمة $n$ حتى 10. جميع النماذج تُضبط للتقليل من الخطأ التربيعي المتوسط.

ما هو التباين؟

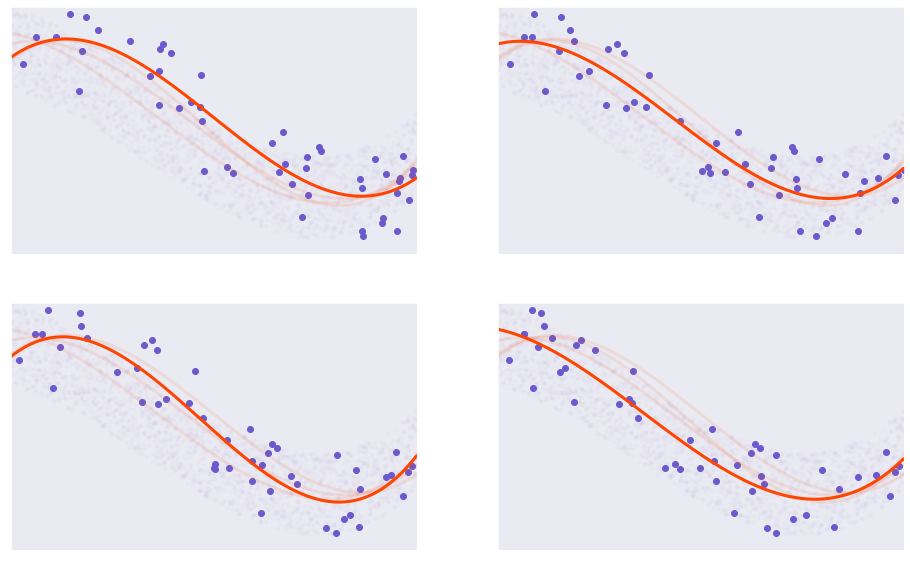
لتعريف التباين ببساطة، ليست كُل العينات لديها نفس الصفات. عندما يكون لدينا عينتين مُختلفتين، فإننا سنبني نماذج مُختلفه قليلاً عن بعضها.

_{تم إختيار خمسين عينة مختلفة من نفس مجتمع البيانات. تم ضبط كُل واحدة بإستخدام نموذج متعدد الحدود للدرجة الثالثة.}

هنا نقول أننا غيرنا في مدخلات النموذج. في الرسوم البيانية السابقة، كل النماذج متعددة الحدود من الدرجة الثالثة $X^3$. كل نموذج دُرب على عينات مختلفة من مجتمع البيانات.

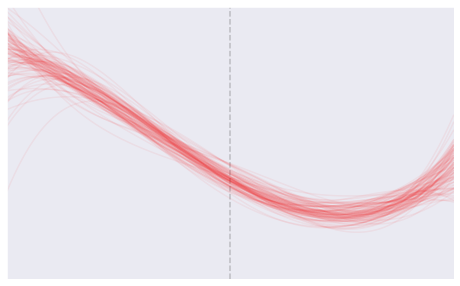
لنتخيل أننا أعدنا هذه العملية 100 مرة. بهذا الشكل ستكون النتيجة:

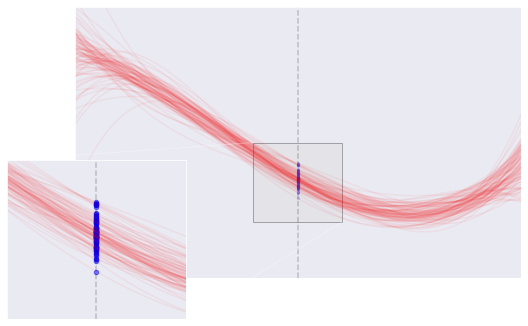
هدف بناء النموذج هو التنبؤ. عندما نريد التنبؤ ب $Y$ بإستخدام النماذج لقيمة $X$ جديدة، سينتج لنا التالي:

_{قيم متغيره لما تم التنبؤ به $Y$ (النقاط باللون الأزرق) بإستخدام النماذج المختلفة. الخط الرصاصي المتقطع هي القيمة $X$ التي إستخدمناها كمدخل للنموذج.}

بعض النماذج تتنبؤ بشكل مختلف جداً، ولكن بعضها يتنبؤ بشكل متسق وثابت. نقوم بتحديد إتساق وثبات النموذج بإستخدام التباين. إحصائياً، التباين للنموذج هو متوسط الانحراف التربيعي لجميع التنبؤات. كما ذُكر في مقدمة في التعلم الإحصائي:

بشكل عام، الأساليب الإحصائية الأكثر مرونة لديها تباين عالي.

ما هو الإنحياز؟

بعد ان بنينا أكثر من نموذج تنبؤ، نريد أيضاً معرفة المتوسط، أو القيمة المتوقعة من النموذج. هذا المتوسط يطلق عليه القيمة المتوقعة للتنبؤات. الإنحياز هو مدى اختلاف القيمة المتوقعة لكل التنبؤات عن القيم الحقيقية.

_{الإنحياز هو المسافة بين القيم الحقيقية (المثلث البنفسجي) والقيم المتوقعة (الخط الأزرق). التباين هو مدى عرض النتائج المتوقعة (باللون الأحمر).}

الرسم البياني السابق يظهر طريقة قياس الإنحياز والتباين وكيف يتم إستخدام كُلِ منهما لوصف النماذج التي تكون فارطة بالتخصيص أو التعميم.

في نموذج الإنحدار الخطي ( $n=1$ )، المتوسط لنموذج التنبؤ مختلف جداً عن القيمة الحقيقة لـ $Y$. ايضاً تباين النموذج عالي. لذا يمكننا القول أن نموذج الإنحدار الخطي لدية إنحياز عالي و تباين عالي.
في النموذج $n=7$، متوسط التنبؤ قريب جداً من القيمة الحقيقة لـ $Y$. ولكن، تباين النموذج عالي. هنا يمكننا القول أن النموذج لدية إنحياز منخفض و تباين عالي.
في النماذج $n=2$ و $n=3$، الإنحياز والتباين منخفضان. الهدف في النماذج الإحصائية هي الوصول إلى نماذج لديها إنحياز وتباين منخفضة.

المقايضة بين الإنحياز والتباين

كيف نعرف مدى صحة نتائج النموذج؟ يمكننا قياس الخطأ بين القيمة المتوقعة والقيمة الحقيقة، ثم جمعها وحساب متوسطها. بذلك، نصل إلى إنحياز نموذج التنبؤ. ولكن، سيؤثر ذلك بشكل عكسي، فإذا كان الإنحياز يساوي 0، ذلك يعني أن النموذج يتنبؤ بكل شئ بشكل صحيح (بدون تباين) أو أن النموذج يتنبؤ بشكل خاطئ لكل القيم (تباين عالي). بدلاً من ذلك، نقوم بجمع إما القيمة المطلقة أو القيمة التربيعية للخطأ. القيمة التربيعية للخطأ هي الأفضل في كثير من الحالات كونها اسهل بالتنفيذ والوصول إلى النتائج. نطلق على ذلك متوسط الخطأ التربيعي (MSE):

\[MSE = \frac{\sum_{n} ( \hat f_{x_0} - f_{x_0} )^2}{n}\]

إذا درست الإحصاء، فستعلم أن هذة المعادلة يطلق عليها القيمة المتوقعة لتربيع الخطأ. لدى القيمة المتوقعة بعض الخصائص التي يمكن استخدامها للوصول إلى متوسط الخطأ التربيعي. يمكن الوصول لشرح لها في ويكيبيديا أو هذا المقال.

$MSE = var(\hat f_{x_0}) + (E[\hat f_{x_0}] - f_{x_0})^2 + var (\epsilon^2)$ $= var(\hat f_{x_0}) + bias(\hat f_{x_0})^2 + var (\epsilon^2)$

المصطلح $var (\epsilon^2)$ يقصد به الخطأ الغير قابل للإختزال. يحدد القيمة الدنيا للخطأ التربيعي المتوسط للنموذج.

كتمرين رياضي، هل يمكنك حساب الخطأ الغير قابل للإختزال بمعرفتك بأن قيمة الخطأ بين $[-10, 10]$؟

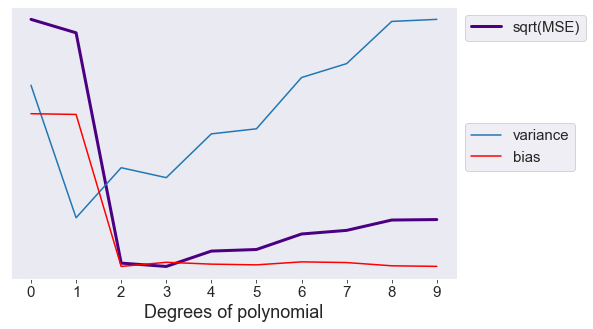
من الواضح أن قيمة متوسط الخطأ التربيعي تعتمد على مجموع و إنحياز نموذج التنبؤ. إذا قمنا برسم متوسط الخطأ التربيعي، التباين والإنحياز مع بعضها البعض للنماذج وقمنا بزيادة تعقيدها كل مره، سيظهر لنا رسم بياني على شكل حرف $U$ للخطأ التربيعي المتوسط. إختيار النموذج المثالي يعتمد على إختيار القيم المناسبة للإنحياز والتباين.

هذا ما يطلق عليه — مقايضة الإنحياز والتباين. في مثالنا، يكون متوسط الخطأ التربيعي في قيمتة الدنيا عندما تكون $n=3$. يمكننا القول أن متعددة الحدود من الدرجة الثالثة هي أفضل نموذج يشابهة المجتمع الحقيقي للبيانات.

سؤال: ماذا سيحدث للإنحياز والتباين عند زيادة بيانات التدريب؟

بشكل بديهي، عند زيادة عدد بيانات عينة التدريب، فأن نتائج النموذج ستكون أكثر دقة. لذا، سيكون تباين النموذج أقل عند زيادة عدد بيانات التدريب. ولكن على العكس، الإنحياز سيبقى كما هو. يعود ذلك إلى أن الإنحياز يتجه نحو المتوسط أياً كان عدد بيانات عينة التدريب. في الواقع، إذا كانت بيانات التدريب قليله جداً، فأنها ستأثر على إنحياز النموذج لأن الزيادة في عدد البيانات سيجعل نتائج التنبؤ أفضل.

سؤال: ماذا سيحدث للإنحياز والتباين عند إضافة قيمة غير متغيرة للنموذج؟

بكل بساطة، يقيس التباين مدى توسع تنبؤات النموذج. عند إضافة قيمة ثابتة، فأن التوزيع سيبقى مثل ما هو وتبقى قيمة التباين كما هي. على عكس ذلك، الإنحياز سيتغير إلى إتجاه القيمة الغير متغيرة.

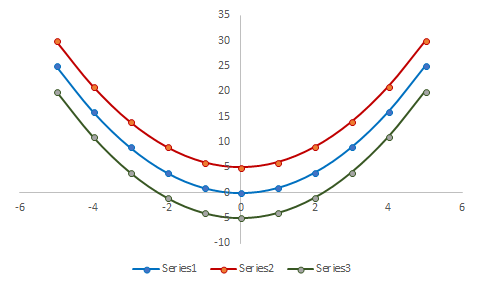مثال: عند إضافة قيمة غير متغيره 5 (اللون الأحمر)، صفر (اللون الأزرق)، -5 (اللون الأخضر). المصدر

الإستعمالات

حتى الآن، اتمنى أن تكون وصلت لك فكرة الإنحياز والتباين. بالأخص، سبب إستخدامها الدائم لوصف أداء النماذج. قد تتسائل ما إذا كانا فقط كلمات لوصف اداء النماذج دون أهمية نظرية أو عملية. هنا، سأشرح لك تطبيق الإنحياز والتباين على التحقق المتقاطع “Cross-Validation”.

التحقق المتقاطع

يعتبر التحقق المتقاطع أحد أشهر الطرق لتقييم أداء النموذج، في العادة، لتقييم أداء النموذج، نقوم بتقسيم البيانات إلى بيانات تدريب وإختبار، نعدل من مدخلات النموذج بإستخادم بيانات التدريب ثم نقيم النتائج بناءًا على بيانات الإختبار. لكن، إذا كان حجم البيانات لدينا قليل، يمكنك تدريب النموذج أكثر من مره بتوزيع البيانات إلى مجموعات صغيرة. ويكون التقييم النهائي للنموذج بناءًا على جميع التقييمات السابقة التي تمت على مجموعات بيانات الإختبار. عند النظر إلى طريقة استخراج العينات، يمكنك معرفة علاقة ذلك مع تباين النموذج. هدفنا هو إيجاد النموذج ذو أقل قيمة لمتوسط الخطأ التربيعي على بيانات تدريب إختبار جديدة، لذا هل سيساعدنا التحقق المتقاطع على فعل ذلك؟

أولاً، لنأخذ طريقة إختبار النموذج بإستخدام مجموعة اختبار واحدة (LOOCV)، في هذة الطريقة، بيانات الإختبار عبارة عن مجموعة واحد فقط، وبيانات التدريب هي باقي البيانات. يتم تدريب النموذج بشكل متكرر بعدد $n-1$ مره، في المعادلة $n$ هي عدد البيانات. التقييم النهائي للنموذج هو متوسط جميع بيانات التدريب.

بشكل مباشر، يمكنك ملاحظة فوائد طريقة LOOCV عكس الطريقة البسيطة لتقسيم البيانات إلى بيانات تدريب واختبار بدون تحقق متقاطع. إذا كانت عينة البيانات جيدة، فأن اخذ العينات بشكل متكرر من بيانات التدريب سيكون نتائجة مشابه لأخذ العينات من مجتمع البيانات الحقيقي. ولكن الفرق الملاحظ هو أنه عند تطبيق LOOCV، جميع عينات التدريب ستتداخل على بعضها البعض. هذا التداخل سيسبب تباين عالي للنموذج.

للتقليل من التباين، هناك طريقة أخرى يمكن إستخدامها يطلق عليها التحقق المتقاطع بإستخدام K-Flod. فيها، يتم تقسيم العينة إلى عدد متساوي $k$. فيها بيانات الإختبار مجموعة واحدة والباقي بيانات تدريب. يتم تدريب النموذج بعدد $k$ مره، في كل مره يتم تغير مجموعة بيانات الإختبار.

المصدر

بالمقارنة مع LOOCV، طريقة K-Flod بإمكانها إيجاد نماذج بتباين منخفض، ولكن بإنحياز مرتفع.

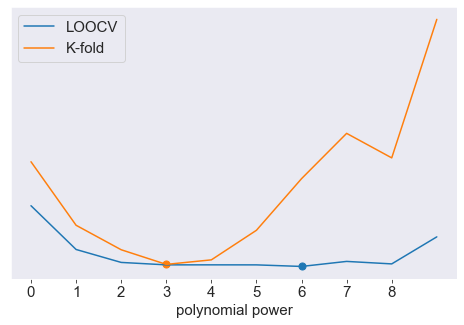
_{نتيجة متوسط الخطأ التربيعي بإستخدام التحقق المتقاطع LOOCV و K-Fold على بيانات الإختبار.}

مدى فائدة إستخدام التحقق المتقاطع لإختيار أفضل النماذج؟ هنا، سنحاول اختيار أفضل قوة لمتعددة الحدود بإستخدام التحقق المتقاطع K-Fold ( $K=10$ ). نتائج LOOCV كانت أفضل عند القوة 6 بينما كانت أفضل قوة لـ K-Fold عند الرقم 3. إذا أردنا أن لا يكون نموذجنا فارط بالتخصيص على بيانات التدريب، فسنختار النموذج الأبسط عند $n=3$.

النتيجة

أتمنى أن المقال ساعدك على فهم المزيد عن ما وراء فكرة الإنحياز والتباين. من الآن وصاعداً، عند التفكير بإنحياز وتباين النموذج، يمكنك مباشرة البدء بتطبيق المبادئ الأولى والأساسية لإختيار القيم المناسبة للنموذج.

يمكنك التجربة والتعديل على الرسوم البيانية الموجودة في هذا المقال هنا.

جميع الصور والبيانات المستخدمة (عدا أن تم ذكر مصدر لها) انشأت بواسطة الكاتب.

مراجع

James, Gareth, et al. An introduction to statistical learning. Vol. 112. New York: springer, 2013.

المصدر

كُتب في 09/09/2022