هذه السلسلة من المنشورات ستكون ملخصات خاصه بي كتبتها أثناء دراستي لكورس Udacity في علم البيانات أحببت أفيد فيها المهتمين ومن يرغب بدخول مجال علم البيانات. قبل البداية يتوقع منك أن تكون لديك معرفة سابقة بلغة البرمجة بايثون وبعض مكاتبها المخصصه لعلم البيانات مثل scikit-learn.

الجزء الأول يشمل التالي:

• Machine Learning Bird’s Eye View
• Linear Regression

الفصل الأول - التعلم الموجَّه Supervised Learning

الدرس الأول - معلومات عامة عن تعلم الآلة Machine Learning Bird’s Eye View

توجد ثلاث انواع من تعلم الآلة

1- التعلم الموجَّه Supervised Learning

في التعليم الموجَّه، تتعلم الخوارزمية من البيانات التي لدينا ومن نتائجها، بعد أن تدرسها الخوارزمية، تستطيع توقع نتائج أي قيمة تقدم لها.

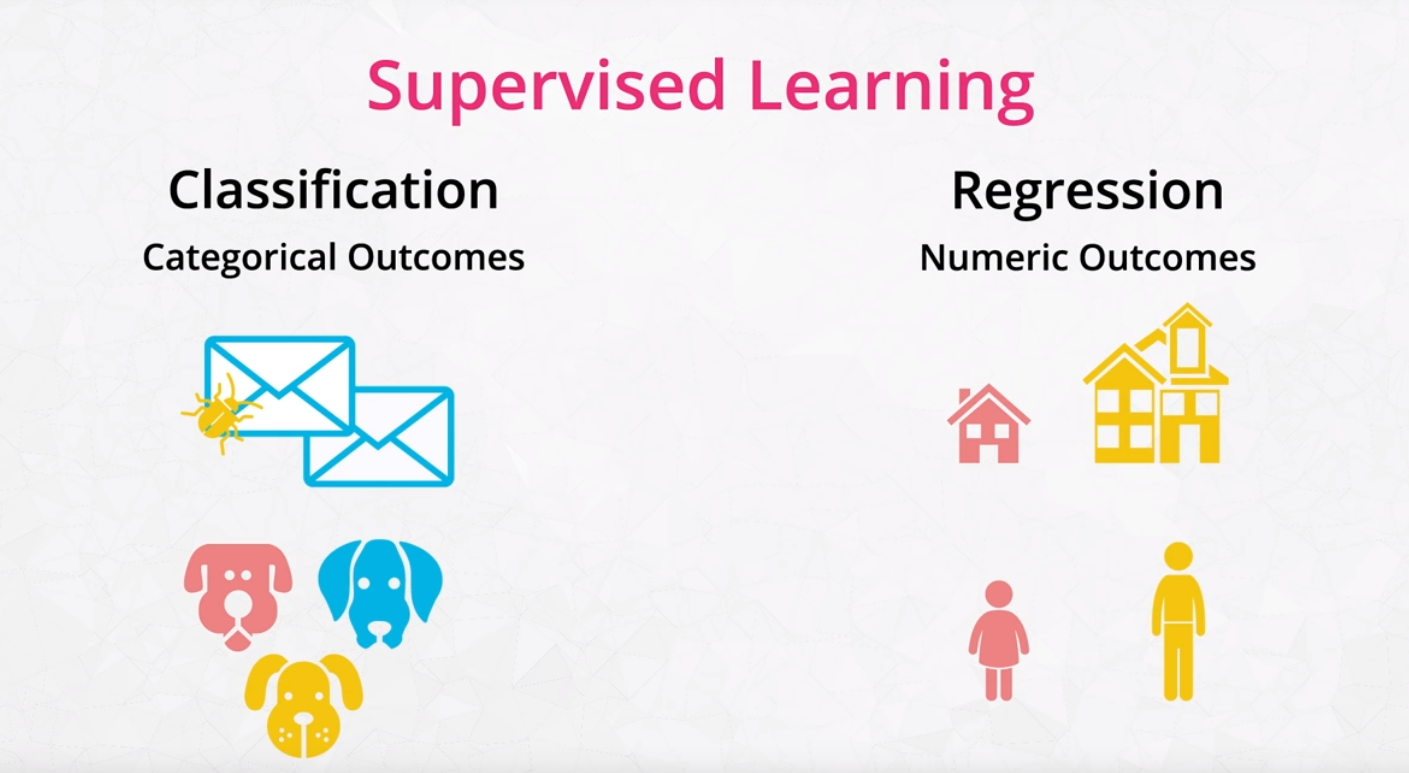
ينقسم التعليم الموجة إلى قسمين:

• Classification التصنيف: يستخدم لتوقع الفئة التي تنتمي لها البيانات. أو للنتائج التي لها خيارين. مثلاً ما إذا كانت رسالة البريد الإلكتروني مزعجة أو لا.
• Regression الإنحدار: تستخدم لتوقع نتائج رقمية مثل أسعار المنازل.

لمزيد من المعلومات عن التعلم الموجَّه سبق أن شرحته بشكل مفصل هنا.

2- التعلم غير الموجَّه Unsupervised Learning

في التعلم الغير موجَّه، توجد لدينا بيانات بدون نتائج، فتحتاج الآلة للتعلم بنفسها، وتوجد أكثر من طريقة مثل تقسيم وتجميع البيانات حسب تشابهها.
شرح أكثر تفصيل عن التعلم غير الموجَّه هنا

3- التعلم التعزيزي Reinforcement Learning

تتعلم الآلة عن طريق عمل نشاطات أو Actions وتلقي نتائج من هذه النشاطات التي فعلتها.
تم شرح التعلم التعزيزي بشكل مفصل في منشور سابق هنا

الفصل الأول - التعلم الموجَّه Supervised Learning

الدرس الثاني - الإنحدار الخطي Linear Regression

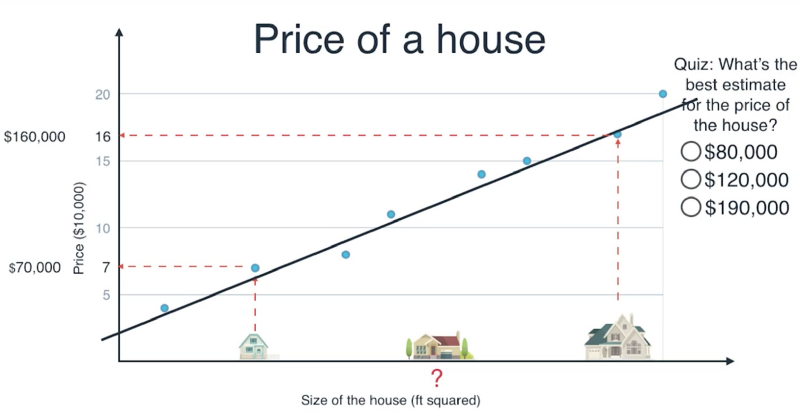
¹ في الصورة السابقة نريد الإجابة على سؤال، كم سيكون سعر البيت، بعد مقارنة النتائج وتحديد حجم البيت مقارنة ببقية البيوت، كم تتوقع يكون سعره؟ الإجابة 120 ألف، وأجبنا عليه بواسطة رسم خط مناسب لكل النقاط (البيوت) التي لدينا في البيانات.

توجد طريقتين لرسم خط بين النقاط، الأولى هي عبر إستخدام Tricks او طرق لتحريك الخط، والثانية عن طريق إستخدام Error Functions وهي طريقة أخرى لموازنة الخط.

الطريقة الأولى Tricks

الهدف من رسم الخط هو ان يكون قريب جداً إلى النقاط ومناسب لهم جميعاً، بالتأكيد توجد طرق كثيره لرسم الخط في حال كانت لدينا نقاط كثيره وقد يناسب بعض النقاط ولكن لن يناسبها جميعها، الهدف هنا رسم خط يناسب الجميع. ويوجد طريقتين لتحريك الخط ²:

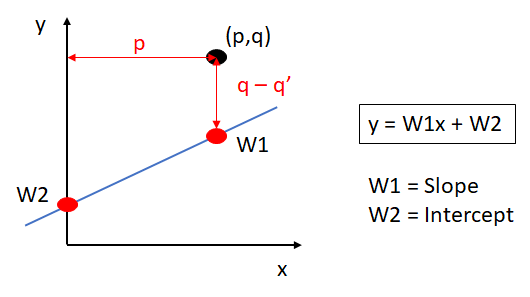
1- Absolute Trick

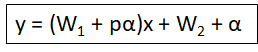
القيمة α هنا تعرف بالـ Learning rate. نقوم بتغيرة ليتغير مكان الخط.
( If the point is below the line, the intercept decreases (subtract from w1 and w2); if the point has a negative x-value, the slope increases. )

2- Square Trick

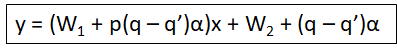
طريقة الحساب:
نفرض لدينا النقطة: (x,y) = (-5, 3)
والمعادله والتي تعني موقع الخط لدينا: y = -0.6x + 4 و α=0.01 في الصورة السابقة q تعني هنا y و q’ نتيجة طرح q-q’.
لإستخارج y للخط نقوم بتعويض x من النقطة في المعادلة y = -0.6x + 4
y = -0.6 (-5)+4 = 7
الآن q-q’ = 3 - 7 = -4
نعوض النتائج لنا في المعادلة
y = (W1 + p (q - q’)α) x + (W2 + (q - q’)α)
y = (-0.6+(-5 * -4 * 0.01))x + (4 + (-4 *0.01)) y = (-0.6+0.2)x + 3.96 y = -0.4x + 3.96

الطريقة الثانية Gradient Descent

طريقة لرسم الخط، في كل مرة تحسب المسافة بين الخط والنقاط، النتيجة من هذه الحسبه هي ما يسمى بالـError وهو مجموع كامل المسافات بين كل نقطة والخط.
وهدف هذه الطريقة هي حسابه في كل مره والمحاولة ان تكون النتجية أقل ما يمكن.

طريقتين لحساب الـError:

1- Mean Absolute Error

مثال:
لدينا هذا الخط y = 1.2x + 2
واعطينا هذه النقاط:
(2, -2), (5, 6), (-4, -4), (-7, 1), (8, 14)
وطلب منا حساب Mean Absolute Error، المعادلة لحسابه هي مجموع المسافات بين النقاط والخط تقسيم عدد النقاط:
اولاً نوجد المسافه بين كل نقطة والخط والطريقة هي اولاً إيجاد y’ بواسطة حل y في معادلة الخط:
مثال لأحد النقاط (-4, -4):
y = 1.2x + 2
y = 1.2*(-4) + 2
y = -4.8 + 2
y = -2.8
ولحساب المسافه بين الـy الخط و y النقطة نقوم بالتالي:
Error = -2.8 - -4 = 1.2
ملاحظة: إذا كانت النتيجة بالسالب نأخذ القيمة المطلقة.
النتيجة:
(6.4 + 2 + 1.2 + 7.4 + 2.4) / 5 = 3.88

2- Mean Squared Error

بنفس الطريقة السابقة، لكن هذه المرة ترسم مربعات من المسافه بين النقطة والخط، والعملية الحسابية تكون بحساب مساحة كل مربع وأخذ المتوسط.
نأخذ النتيجة النهائية لمسافة النقاط من المثال السابق:
(6.4, 2, 1.2, 7.4, 2.4) ونربع كل واحدة
(40.96, 4, 1.44, 54.76, 5.76) بعد ذلك نضرب قسم المجموع على عدد النقاط:
(40.96 + 4 + 1.44 + 54.76 + 5.76) / 5 = 106.92 / 5 = 21.38

أمثلة بايثون و مكتبة scikit-learn

Linear Regression

اذا كان لدينا متغير Feature واحدة

from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd

bmi_life_data = pd.DataFrame.from_csv('data.csv')

bmi_life_model = LinearRegression()
bmi_life_model.fit(x_values, y_values)
laos_life_exp = bmi_life_model.predict([[21.07931]])

x_values = المتغيرات التي نرغب التنبؤ بها
y_values = النتيجة التي نتنبأ عنها

Multiple Linear Regression

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
 
boston_data = load_boston()
x = boston_data['data']
y = boston_data['target']

model = LinearRegression()
model.fit(x, y)
sample_house = [[2.29690000e-01, 0.00000000e+00, 1.05900000e+01, 0.00000000e+00, 4.89000000e-01,
                6.32600000e+00, 5.25000000e+01, 4.35490000e+00, 4.00000000e+00, 2.77000000e+02,
                1.86000000e+01, 3.94870000e+02, 1.09700000e+01]]
prediction = model.predict(sample_house)

Polynomial Regression

نستخدم Polynomial Features لأضافة المزيد من المتغيرات Features. ³

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

train_data = pd.read_csv('data.csv')
X = train_data['Var_X'].values.reshape(-1, 1)
y = train_data['Var_Y'].values

poly_feat = PolynomialFeatures(degree = 4)
X_poly = poly_feat.fit_transform(X)

poly_model = LinearRegression(fit_intercept = False).fit(X_poly, y)

Regularization

طريقة لإضافة المزيد من البيانات لحل مشكلة لدينا أو للتخلص من فرط التخصيص Overfitting ⁴

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso

train_data = train_data = pd.read_csv('data.csv', header = None)
X = train_data.iloc[:, :-1]
y = train_data.iloc[:,-1]

lasso_reg = Lasso()
lasso_reg.fit(X,y)

reg_coef = lasso_reg.coef_
print(reg_coef)

Feature Scaling

طريقة لإعادة ترتيب البيانات حسب تشابهها، و تستخدم أيضاً للتخلص من البيانات الشاذة. ⁵

• Standardizing: تستخدم عندما يكون لدينا الكثير من البيانات الشاذه.
• Normalizing: تحول فيها البيانات إلى ارقام من 0 إلى 1.

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso

train_data = train_data = pd.read_csv('data.csv', header = None)

X = train_data.iloc[:, :-1]
y = train_data.iloc[:,-1]

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

lasso_reg = Lasso()

lasso_reg.fit(X_scaled, y)

reg_coef = lasso_reg.coef_
print(reg_coef)

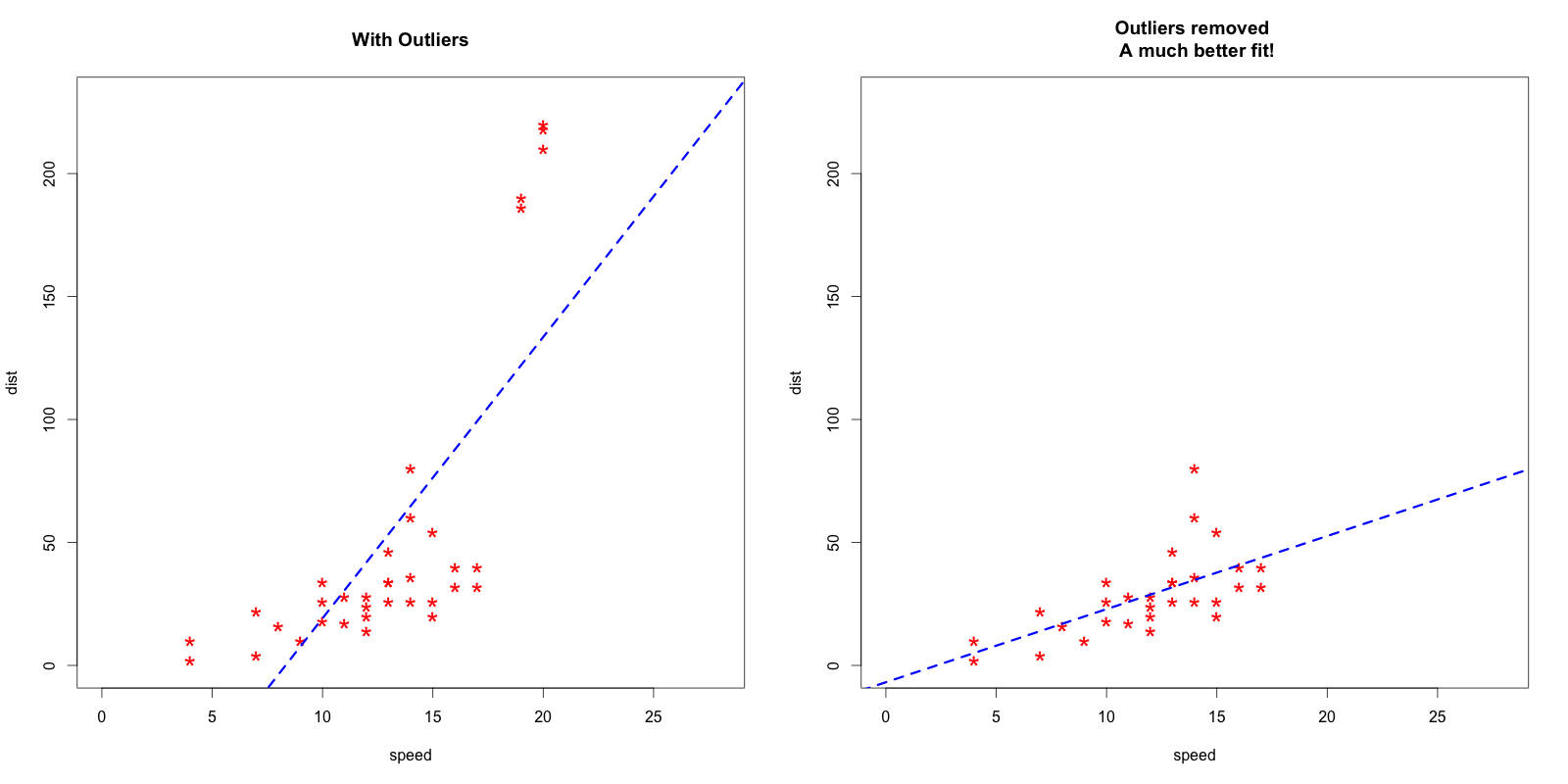
نقطتين مهمه عن Linear Regression

• الإنحدار الخطي يظهر قوته عندما تكون البيانات خطية أو على شكل خط.
• الإنحدار الخطي يتأثر بالبيانات الغربية أو الخارجه عن المألوف Outliers، مثال: ⁶

الإنتقال إلى ملخص كورس علم البيانات - 2