تحدثت في المنشور السابق عن الطرق التي تتعلم بها الآلة، البعض يضيف إليها الشبكات العصبيه (Neural Networks) والتعلم العميق (Deep Learning) ولكن أرى أن هذه مواضيع كبيره أخرى من الممكن التعمق فيها لوحدها. لنعود لعلم الآلة وطُرق تعلمها، لنتحدث بتفصيل أكثر عن كل طريقة ومتى نستخدمها، وما هي خوارزمياتها.

التعلم الموجَّه (Supervised Learning)

كما عرفناها سابقاً، التعلم الموجَّه يعتمد على البيانات المُعلمّة (Labeled Data) وهي بيانات عرفناها وحددنا نتائجها مُسبقاً، ويندرج تحت التعلم الموجَّه نوعين من طُرق التعلم:

• (Classification) التصنيف: البيانات التي نتائجها مقسمة إلى فئات (Categories) .مثل الجنسية، اللون، التخصص.
• (Regression) الإنحدار: البيانات التي نتائجها رقمية مثل درجات الحرارة، الطول والوزن.

(Classification) التصنيف

يقوم التصنيف بتقسيم البيانات حسب خصائص معينة معروفة مسبقاً، مثل اللون في الفواكة، نوع الشركة المصنعه في السيارات. من الخوارزميات المستخدمة في التصنيف:

• (Support Vector Machines) آلة المتجهات الداعمة:
  تعتبر من أكثر الخوارزميات استخداماً في التصنيف، وتقوم الخوارزمية بالبحث عن افضل طريقة لتقسيم البيانات. بحيث تحاول تكوين أكبر مسافه بين القيم. ¹
  
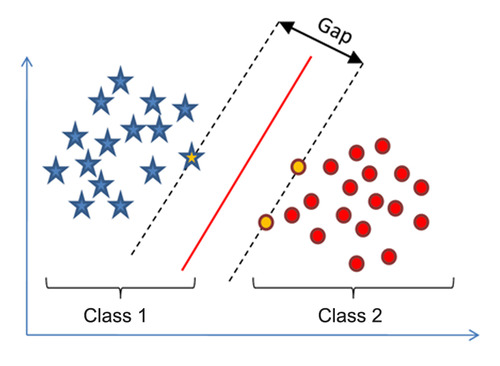
  تقوم الخوارزمية برسم خط فاصل بين القيم، يكون الخط هو أطول مسافه فاصلة بين القيم حسب التصنيف، يمكن بالتأكيد رسم الخط بأكثر من طريقة، لكن الخوارزمية تحاول إيجاد الخط الوحيد الذي يفصل بينهما ويكون الأكبر من حيث المسافه بين القيم. تسمى النقاط باللون الأصفر (Support Vectors) ويكون الإعتماد عليها في قرار المسافه بين خط الفصل والقيم كونها الأقرب له. ²

• (Decision Tree) شجرة القرار:
  خوارزمية شجرة إتخاذ القرار تستخدم أمر الشرط (If-then) وتستخدم بشكل أكثر في البيانات ذات الفئات (Categorical)، لنأخذ مثال لتتضح الصورة أكثر:
  
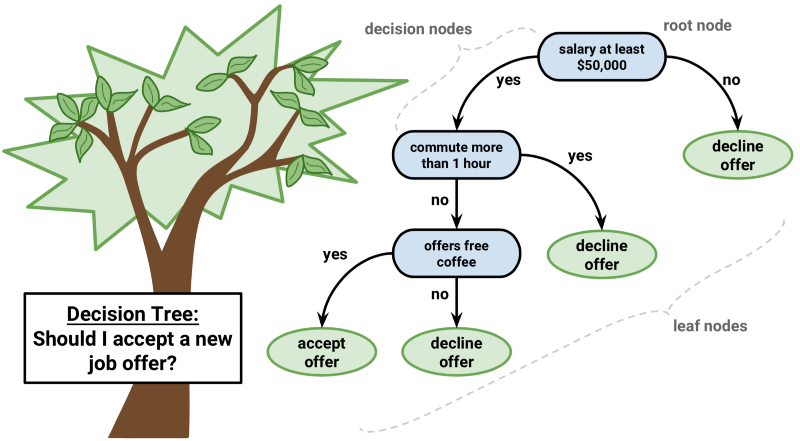
  في الصورة أعلاه استخدمنا (Decision Tree) لإجابة سؤال: هل أوافق على العرض الوظيفي؟ قمنا بطرح أسئلة إجاباتها بنعم أو لا، وفي كل مرة نجيب بنعم ننشأ فرع جديد للشجره ونطرح سؤال فرعي آخر يحمل نفس الإجابة بنعم ولا. تتعلم الآلة الأسئلة عن طريق البيانات التي دربناها عليها (Training Data)، في هذه الخوارزمية نستطيع تحديد عدد الفروع التي يجب ان نصل لها.
  التقسيم والتفرع في الخوارزمية لا ينحصر على الأسئلة التي إجاباتها نعم أو لا، فمن الممكن ان تكون الإجابات عبارة أسئلة أخرى مثلاً، هل النتيجة أكبر من قيمة معينة أو أقل. ³
  
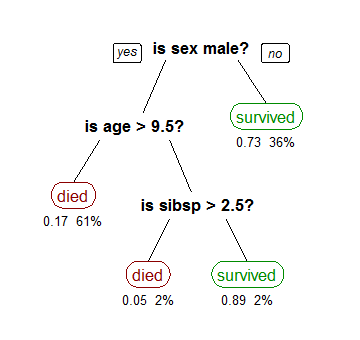
  مثال آخر لإستخدام الخوارزميه، المثال التالي يجيب على سؤال: هل أخرج للعب القولف اليوم أو لا؟
  
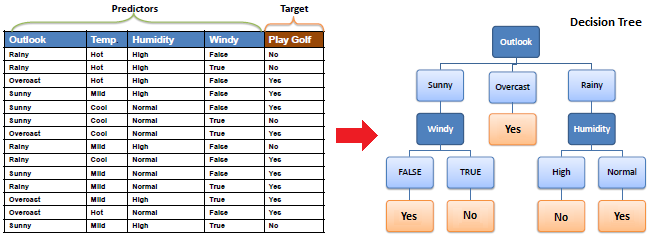
  هنا أعطيت الخوارزمية بيانات للتدريب مع اربع خصائص (Features) والنتيجة لها.
  الـ(Decision Node) هنا (Outlook) ويعني توقعات الرؤية، وهو ما سيتم فصل الشجره عليه، لا يتم إستخدام أي قيمه لعملية الفصل، فتقوم الخوارزمية بعملية حسابية تسمى (Information Gain) تقرر فيها القيمة التي سيتم الفصل عليها بناءاً على أعلى نتيجة.
  
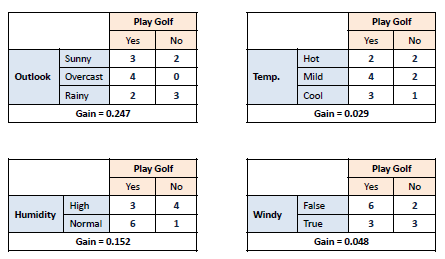
  المعلومات المكتسبة أو (Information Gain) أو (Gain) هي عملية حسابية يتم بواسطتها أكتشاف أكثر الخصائص التي يفضل التقسيم عليها لأنها تقدم لنا بيانات أو معلومات أفضل، تفاصيل أكثر عن طريقة حساب الـ(Information Gain) هنا و هنا. بعد إختيار (Outlook) نقوم بفصل البيانات حسب المتغيرات بداخلها.
  
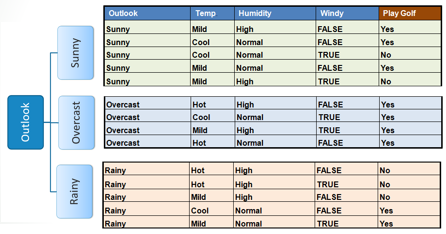
  كل قيمة لديها نتيجة أما نعم للعب القولف أو لا.
  
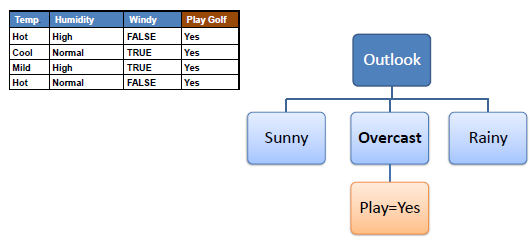
  اذا كانت النتائج دائماً نعم، فلا نقوم بالفصل أكثر.
  
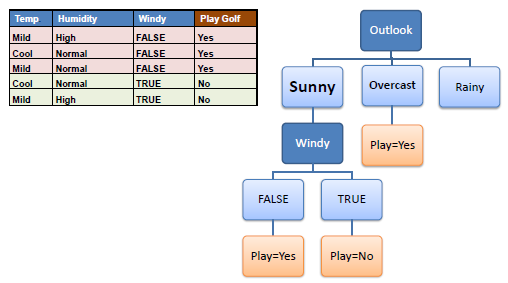
  أما أذا كان لدينا أكثر من نتيجة فنبدأ بحساب الـGain مره أخرى على الخصائص المتبقية ونختار أكبر قيمة مرة أخرى ونبدأ بالفصل عليها وهكذا. ^{4 5}

• (Logistic Regression) انحدار لوجستي:
  تُستخدم هذه الخوارزمية لتوقع إحتمالية (Probability) لحدوث نتائج معينة وتكون القيمة المتغيرة المدخلة على الخوارزمية على شكل فئات (Catagorical). ويمكن تقسيم نتائج أو مخرجات الخوارزمية إلى ثلاث أنواع بناء على السؤال الذي نريد إجابته أو المشكلة المراد حلها:

  • (Binomial): وهي النتائج التي من نوعين، أما نعم أو لا، 0 أو 1، صح أو خطأ وغيرها.
  • (Multinomial): ويمكن أن تكون النتائج أكثر من 3 ولا تكون محددة بترتيب معين.
  • (Ordinal): وهي مشابهه للـ(Multinomial) ولكن تكون مرتبه مثلاً: 0، 1، 2، 3.
    مثلاً، شركه تأمينات تملك بيانات فيها عمر الشخص وما ذا كان يملك تأميناً أو لا: ⁶
    
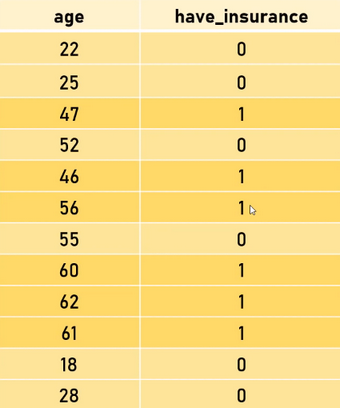
    وعند محاولة رسم البيانات وتفعيل الخوارزمية عليها مع حد Threshold = 0.5 ستكون شكلها كالآتي
    
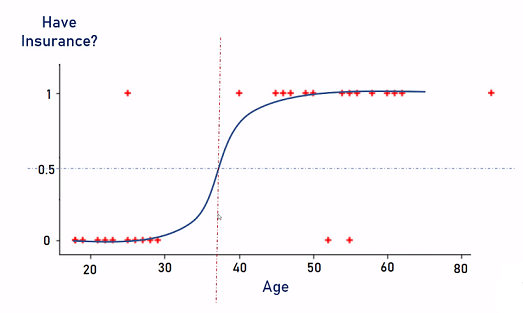
    الخط هنا يعرف بدالة سيجمويد (Sigmoid Function) وهي طريقة لتحويل المدخلات إلى رقم بين 0 و 1. ⁷

(Regression) الإنحدار

كما ذكرنا سابقاً، نستخدم الإنحدار عندما تكون النتائج المتوقعه رقمية مثل أعمار أشخاص أو سعر سهم وغيرها. الوظيفة من الإنحدار هي توقع رقمي لشئ ما بناءاً على المدخلات. ذكرت في المنشور الأول مثال عن الإنحدار في تنبؤ أسعار السيارات. ويوجد نوعين من خوارزميات الإنحدار:

• (Linear Regression) إنحدار خطي: فيها يكون لدينا بيانات ونتائج، والهدف هو التنبؤ بنتيجة قيمة جديدة غير معرفة سابقاً بأقل الأخطاء، وبناءاً على البيانات المعطاة سابقاً. ⁸
• (Polynomial Regression) الإنحدار المتعدد: ولا يتم هذا الإنحدار إلا أذا كانت البيانات خطية، ويعتبر إستخدامه محدد ولا يتم إلا في حالات خاصة.
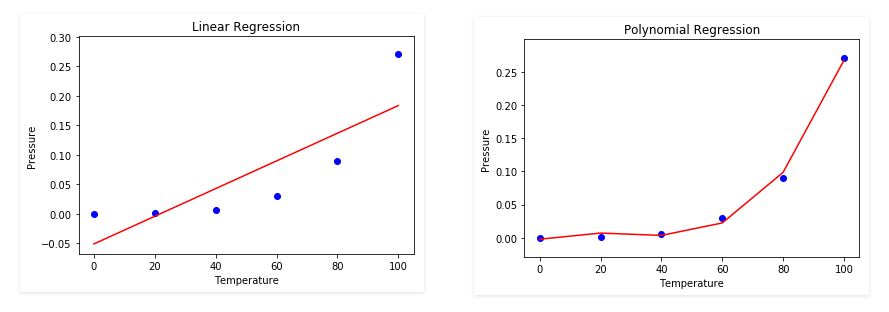
  في الرسم البياني أعلاه، أستخدمنا نفس البيانات ورسمناها بطريقتين، إنحدار خطي ومتعدد، ويظهر أنها في كلا الحالتين اظهرت نتائج كون كما ذكرت سابقاً، ليتم تكوين إنحدار متعدد يجب أن يتم تشكيل إنحدار خطي أولاً. أمثلة على الإنحدار الخطي والمتعدد.

---

العودة إلى تعلم الآلة للجميع - 2 - الإنتقال إلى تعلم الآلة للجميع - 4