📝 ملخص كورس علم البيانات - 10
هذا الملخص عن مكتبة PyTorch، مكتبة أخرى متخصصة للشبكات العصبية في بايثون.
الفصل الثاني - التعلم العميق Deep Learning
الدرس الخامس - Deep Learning with PyTorch
الدرس عملي بشكل كامل، لذا سأضع بعض الأمثلة لطريقة إنشاء شبكات عصبية في PyTorch.
عملية الحساب
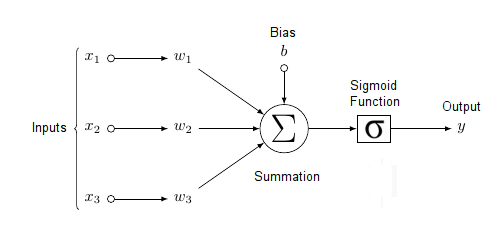
طريقة الحساب (مثال على الصورة العلوية) في الشبكة العصبية كالتالي:
- لدينا في الـLayer الأول ثلاث مدخلات Features ( Inputs ) ( x1, x2, x3 ) إضافة إلى الـBias وهي 1 هنا.
- كل مدخل لدية Weight ( w1, w2, w3, w4 ).
- يضرب كل Input على كل Weight ينتمي له ( x1 * w1, x2 * w2, x3 * w3 )
- تجمع نتائج عمليات الضرب السابقة ويضاف إليها الـbias (b) وتطبق عليها دالة معينة مثل Sigmoid وتخرج لنا نتيجة.
- دالة Sigmoid:
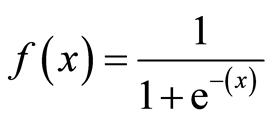
- نضيف النتيجة التي حصلنا عليها هنا بدلاً من x في الدالة السابقة وهي النتيجة النهائية للشبكة .
Tensor
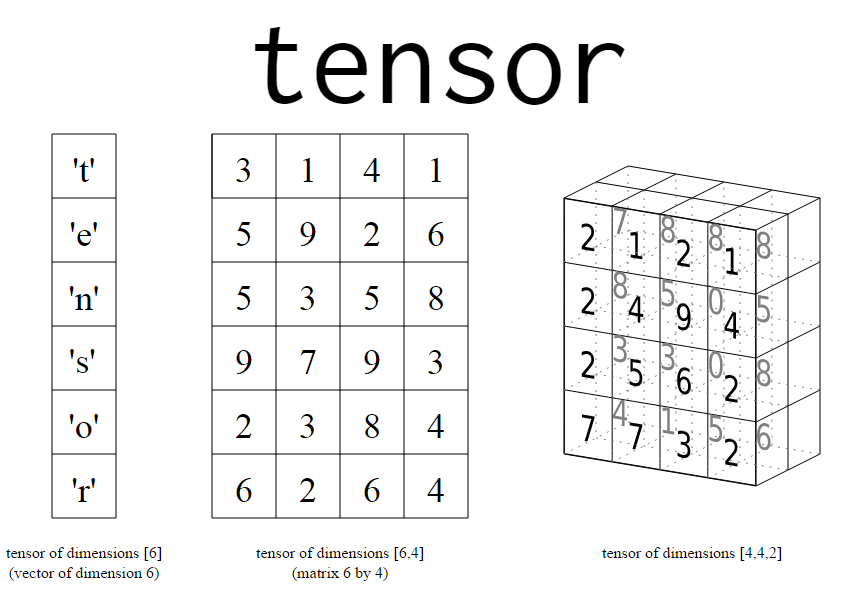
كل ما يكون ويدخل في الشبكة العصبية عبارة عن Tensor، بمعنا أصح، اي شئ نريد إختبارة في الشبكة يجب أن نحولة إلى Tensor من أرقام.
طريقة تصميم شبكة عصبية في Pytorch
شبكة عصبية بـLayer واحد.
import torch
# دالة Sigmoid
def activation(x):
""" Sigmoid activation function
المدخل لها هو دائماً نتيجة الشبكة
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
# بما اننا سنقوم بتصميم شبكة عصبية من ارقام عشوائية
# نريد مع كل تشغيل للشبكة تكون الأرقام نفسية لنتحقق
# من نتائج بيانات التدريب والإختبار، لذا وضعنا هذه الدالة manual_seed
torch.manual_seed(7)
# هذا الأمر سيكون Tensor بعامود واحد وخمس اسطر
features = torch.randn((1, 5))
# سنجعل البرنامج يكون لنا Weight بشكل عشوائي
# ولكن ستكون بنفس مقاسات المدخلات لدينا ونستخدم randn_like لتكوينها
weights = torch.randn_like(features)
# كذلك ال bias ولكن ستكون منفصلة عن البقيه في Tensor وحيدة 1×1
bias = torch.randn((1, 1))
# للقيام بالعملية الحسابية التي شرحتها مسبقاً نقوم بالتالي
# عملية الضرب features * weights
# المكتبة pytorch بنفسها عندما تقوم بعملية الضرب تضرب كل قيمة بما يقابلها
# x1 * w1 , x2 * w2 .. etc
# نجمع كل نتائج عمليات الضرب بواسطة .sum()
# ثم نضيف لها الbias ونقوم بحساب Sigmoid من الدالة التي سبق ان عرفناها
y = activation((features * weights).sum() + bias)
# أو
# y = activation(torch.sum(features * weights) + bias)
# كلا الخطوتين صحيحة
print(y)
# يمكن إختصارها أكثر أيضا عن طريق matrix multiplication
# بواسطة torch.mm() والتي تقوم بعملية الضرب والجمع في خطوة واحدة
# ولذلك نحتاج لتغير شكل الـWeight بدلاً من أن تكون 1×5 (عامود واحد وخمس اسطر)
# ليكون 5×1، (خمس عواميد في سطر واحد)
# توجد ثلاث طرق للتحويل في pytorch:
new_weights = weights.view(5,1) # أو weights.reshape(5, 1) أو weights.resize_(5, 1)
# وللتأكد أننا نحصل على نفس النتائج بالعملية السابقة نقوم بإختبارها كالتالي
print(activation(torch.mm(features, new_weights) + bias))
مثال آخر لشبكة عصبية مضاف لها Hidden Layer مكون من مدخلين اثنين وشكلة كالتالي:
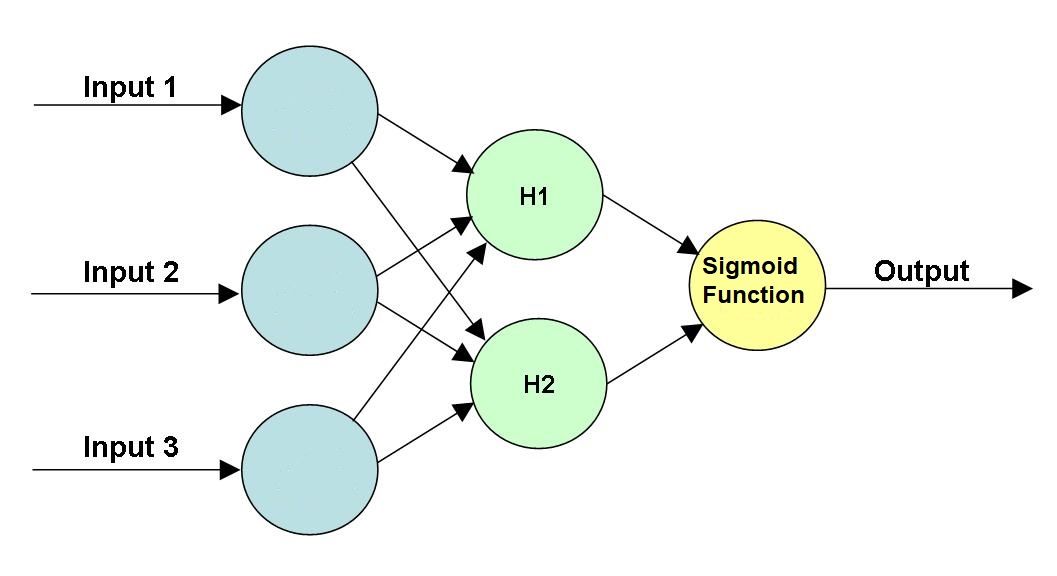
# بنفس الطريقة بالمثال السابق ننشأ الشبكة ونعطيها مدخلات
torch.manual_seed(7)
features = torch.randn((1, 3))
# نحدد مقاسات كل layer
# عدد المدخلات يجب أن يساوي عدد الfeatures هنا 3
n_input = features.shape[1]
# عدد المدخلات في الHidden Layer (الأخضر في الصورة العلوية)
n_hidden = 2
# عدد النتائج أو المخرجات
n_output = 1
# نحدد الـWeights للجزء الأول من المدخلات إلى Hidden Layer
W1 = torch.randn(n_input, n_hidden)
# ومن الHidden Layer إلى المخرجات
W2 = torch.randn(n_hidden, n_output)
# كذك الbias لكلا الخطوتين
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
# ونحسب النتيجة كالتالي
hidden_layer = activation(torch.mm(features, W1) + B1)
y = activation(torch.mm(hidden_layer, W2) + B2)
print(y)
للتحويل من مصفوفة في numpy إلى tensor في pytorch نقوم بالتالي
import numpy as np
a = np.random.rand(4,3)
# الآن b هي tensor بنفس شكلها في numpy
b = torch.from_numpy(a)
print(b)
# ولعرض شكلها كما في numpy
print(b.numpy())
هذا مثال بسيط لطريقة تشكيل شبكة عصبية وحساب نتائجها. كل الأمثلة على نفس البيانات:
NN in Pytorch
تسهل Pytorch عملية إنشاء الشبكات العصبية عند إستخدام مكتبة nn التابعة لها. مثال:
from torch import nn
import torch.nn.functional as F
class Network(nn.Module):
def __init__(self):
# نحتاج السطر الأول دائماً إذا أردنا العمل بهذه الطريقة، كي يتعرف Pytorch
# على اننا ننصمم شبكة عصبية بعدة layers
super().__init__()
# Input ---> hidden layer
self.hidden = nn.Linear(784, 256)
# Hidden ---> Output layer
self.output = nn.Linear(256, 10)
def forward(self, x):
# مررنا نتيجة الـ input ---> hidden layer إلى دالة sigmoid
x = F.sigmoid(self.hidden(x))
# مررنا نتيجة الـ hidden ---> output layer إلى دالة sigmoid
x = F.softmax(self.output(x), dim=1)
return x
مثال آخر:

طريقة تكوين هذه الشبكة العصبية في بايثون و pytorch كالتالي:
from torch import nn
import torch.nn.functional as F
class Network(nn.Module):
def __init__(self):
super().__init__()
self.h1 = nn.Linear(784, 128)
self.h2 = nn.Linear(128, 64)
self.output = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.h1(x))
x = F.relu(self.h2(x))
x = F.softmax(self.output(x), dim=1)
return x
model = Network()
model
في الملخص السابق استخدمت Sequential، وهي نفسها سنستخدمها هنا، لتكوين شبكة عصبية كاملة، وطريقتها كالتالي
# نعرف المدخلات وحجمها
input_size = 784
hidden_sizes = [128, 64]
output_size = 10
# هنا عرفنا Sequential وبدأنا بداخلها بتعريب الـLayers
# واحد تلو الآخر كما في الأمثلة السابقة.
model = nn.Sequential(nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
nn.Linear(hidden_sizes[1], output_size),
nn.Softmax(dim=1))
print(model)
تدريب الشبكة العصبية
- Loss function: حساب نسبة الخطأ في التوقعات. نحاول تدريب الشبكة دائماً على أن تكون نتائج الـLoss Function فيها أقل ما يمكن. كل ما قل كل ما كان المودل أفضل.
- Gradient Descent: سبق تحدثت عنها في الجزء الأول، الرابع والثامن، تستخدم في الشبكات ذات التي تحتوي على Layer واحد فقط.
- Backpropagation: بعد مرور البيانات على الشبكة العصبية والحصول على نتيجة الـLoss، تعود بنفس الطريقة إلى الـWeight للمدخلات وتحاول التقليل منه للحصول على أقل نتيجة للـLoss. تستمر بعمل هذه الخطوات حتى تصل لأقل Loss.
Activation Functions
حتى الآن استخدمنا نوعين، Sigmoid / Softmax. توجد أنواع اخرى مثل Tanh و ReLu. 1 2
تطبيقات عملية كاملة مع الحلول تجدونها هنا، الرابط خاص بالكورس ويحتوي على امثله وشروحات من أبسط الشبكات العصبية إلى شبكات عصبية قادرة على توقع وإظهار نتائج للصور. جميع الأمثلة في صفحات jupyter.
العودة إلى ملخص كورس علم البيانات - 9 - الإنتقال إلى ملخص كورس علم البيانات - 11
