مبادئ وتقنيات علم البيانات
ملحق: مراجعة فضاء المتّجهات
فهرس الفصل:
تعريف المتّجه
تعرف المتّجه بطولها و اتجاهها: 📝
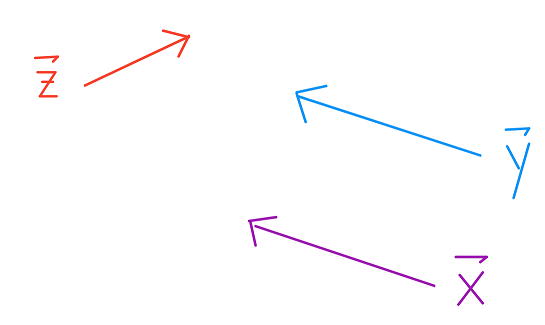
لاحظ أن المتّجه $ \vec{x} $ و $ \vec{y} $ بنفس الطول والاتجاه. لذا هما متجهتان متساويتان.
زيادة المتّجهات
الزيادة في المتّجه يعني التعديل في طولها: 📝
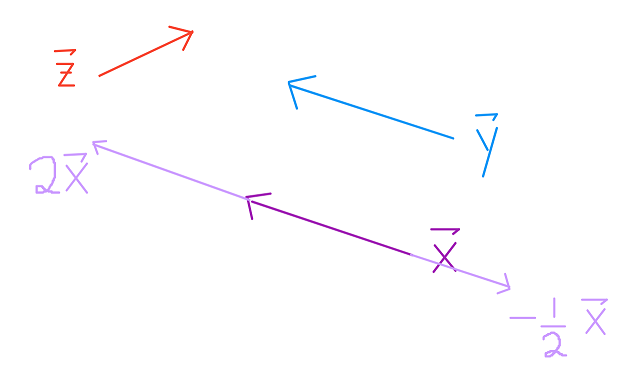
لاحظ أن $ \vec{2x} $ و $ \vec{y} $ لديهما نفس الاتجاه ولكن بأطوال مختلفة. لذا هما غير متساويان.
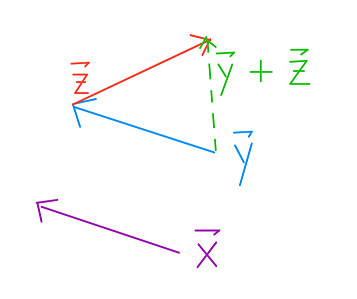
لجمع متّجهتان $ \vec{y} + \vec{z} $، نأخذ خطوة بحسب طول $ \vec{y} $، ثم مباشرة نأخذ خطوة بحسب طول $ \vec{z} $ (أو العكس). يطلق على هذه الخطوات طريقة المثلث، فيها تربط بداية المتّجه الأولى بنهاية المتّجه الثانية.
رموز المتّجهات
يتم تمثيل المتّجهات عادة بالإحداثيات الديكاَرتية Cartesian Coordinates: 📝 📝
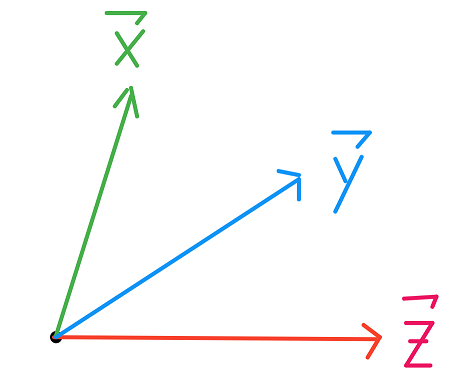
باستخدام هذه الرموز، فإن حساب العملية الرياضية السابقة يصبح سهلاً:
\[\begin{split} \vec{2x} = \begin{bmatrix} 2 \\ 8 \end{bmatrix} , \quad \vec{-0.5z} = \begin{bmatrix} -2 \\ 0 \end{bmatrix} , \quad \vec{2x + -0.5z} = \begin{bmatrix} 0 \\ 8 \end{bmatrix} \end{split}\]
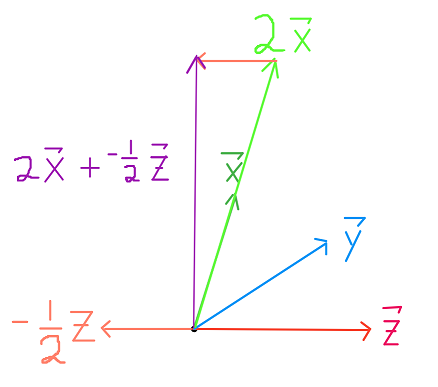
يمكن الزيادة والإضافة في المتّجهات على شكل أجزاء:
\[\begin{split}a \vec{x} + b \vec{y} = \begin{bmatrix} a \ x_1 & + & b \ y_1 \\ & \vdots & \\ a \ x_n & + & b \ y_n \end{bmatrix} \end{split}\]المتّجه 1
في أي مساحة $ d $ للفضاء أو الأبعاد، $ \vec{1} $ هي متّجهة تحتوي على الرقم $ 1 $ مكرراً: \(\begin{bmatrix} 1 \\ \vdots \\ 1 \end{bmatrix}\)
مدى مجموعة من المتّجهات
مدى مجموعة من المتّجهات $ \{\vec{v_1}, \vec{v_2}, \dots, \vec{v_p}\} $ هي جميع التركيبات الخطية المحتملة. لهذه المتّجهات $ p $: 📝
\[\{ c_1 \ \vec{v_1} + c_2 \ \vec{v_2} + \dots + c_p \ \vec{v_p} \ : \ \forall c_i \in F\}\]فيها $ F $ هي مجال فضاء المتّجه.
فضاء المتّجه
فضاء المتّجه $ V $ هو مدى مجموعة من المتّجهات $ \{\vec{v_1}, \vec{v_2}, \dots, \vec{v_p}\} $، فيها كل $ \vec{v_i} $ عبارة عن عمود متّجه بطول $ n \times 1 $. 📝
الفضاءات الفرعية للمتّجه
الفضاء الفرعي $ U $ لـ $ V $ هو مدى مجموعة من المتّجهات $ \{\vec{u_1}, \dots, \vec{u_q}\} $ فيها كل $ \vec{u_i} \in V $. يعني ذلك أن كل متّجه في $ U $ هي أيضاً في $ V $. 📝
الزوايا بين المتّجهات
عند الربط بين نهاية متّجهتان معاً دون التعديل في اتجاهها، يمكن قياس الزاوية بينهما: 📝
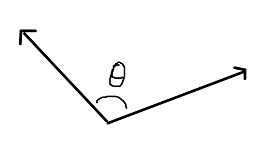
طول المتّجه
الفكرة في $ \mathbb{R}^2 $:
نتذكر طريقة المثلث لجمع متّجهتان. إذا قمنا بإضافة متّجهتان عاموديتان $ \vec{a} + \vec{b} $ في $ \mathbb{R}^2 $، فإننا نعلم أن المتّجه الناتجة هي الوتر. في هذه الحالة، نعلم أيضاً أن طول $ \vec{a} + \vec{b} $ سيكون مطابقاً لنظرية فيثاغورس: $ \sqrt{a^2 + b^2} $: 📝
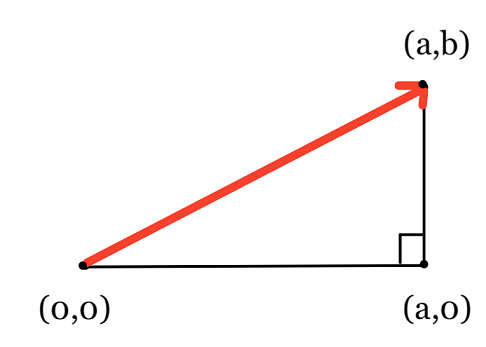
المعادلة العامة لطول $ \vec{v} \in \mathbb{R}^n $:
\[\begin{aligned} || \vec{v} || \quad &= \quad \sqrt{v_1^2 + v_2^2 + \dots + v_n^2} \\ &= \quad \sqrt{\vec{v} \cdot \vec{v}} \end{aligned}\]فيه العامل الأخير هو حاصل عملية الضرب:
\[\begin{split} \begin{aligned} \vec{x} \cdot \vec{y} \quad &= \quad x_1 \ y_1 + x_2 \ y_2 + \dots + x_n \ y_n \\ &= \quad||x|| \ ||y|| \ \cos{\theta} \end{aligned} \end{split}\]التعبير الأول معروف أيضاً بأسم التعريف الجربي للجداء النقطي، والثاني يعرف بالتعريف الهندسي. لاحظ أن نتيجة الضرب هي حاصل الضرب الداخلي المعرف في المتجهات في $ \mathbb{R}^n $
المسافة بين متّجهتان
\[dist(\vec{x},\vec{y}) \quad = \quad || \vec{x} - \vec{y} ||\]
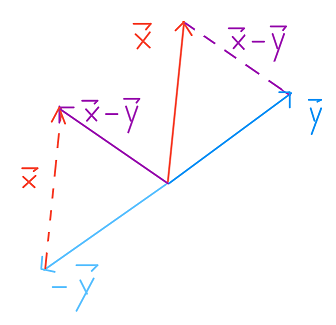
المتّجهات المتعامدة
لمتّجهتان غير صفرية لتصبحان متعامدة، يجب أن يطابقا شرط أن $ \vec{x} \cdot \vec{y} = 0 $. بما أن طولهما لا يساوي صفر، الطريقة الوحيدة لتصبحا المتّجهتان عاموديتان عندما تكون $ \cos{\theta} = 0 $. عندما تكون $ \theta $ تساوي 90 درجة، يكون لدينا ما نعرفه بالزاوية القائمة. 📝
إسقاط المتّجهات
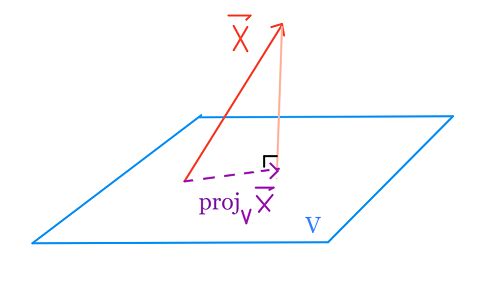
لإسقاط متّجهة $ \vec{x} $ على متّجه أخرى $ \vec{y} $، فنحن نريد إيجاد $ k\vec{y} $ الأقرب إلى $ \vec{x} $: 📝
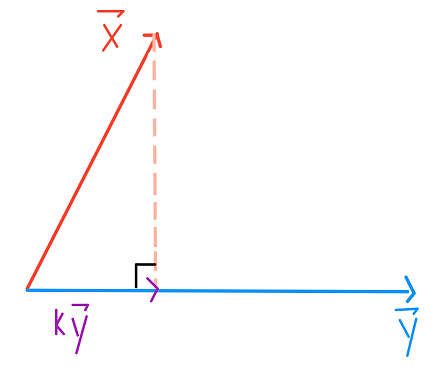
بناءًا على نظرية فيثاغورس، نعلم أن $ k $ يجب أن تكون العدد الذي فيه $ \vec{x} - k \ \vec{y} $ عاموديه إلى $ \vec{y} $، إذاً $ k\vec{y} $ هي الإسقاط (المتعامد) لـ $ \vec{x} $ على $ \vec{y} $.
بنفس الطريقة، لإسقاط متّجه $ \vec{x} $ على أي فضاء المتجهات ممتد بواسطة أي مجموعه من المتّجهات $ \{\vec{v_1}, \vec{v_2}, \dots, \vec{v_p}\} $، فلا نزال نحتاج لإيجاد التركيبات الخطية المحتملة $ \{ k_1 \ \vec{v_1} + k_2 \ \vec{v_2} + \dots + k_p \ \vec{v_p}\} $ الأقرب إلى $ \vec{x} $: