مبادئ وتقنيات علم البيانات
الفصل الرابع عشر: هندسة الخصائص
فهرس الفصل:
مقدمة
هندسة الخصائص Feature Engineering تعني إنشاء وإضافة خصائص جديده للبيانات لزيادة دقة وتعقيد النموذج.
حتى الآن، قمنا فقط بتطبيق الانحدار الخطي باستخدام خصائص كمية كمُدخلات، استخدمنا القيمة الكمية لمجموع الفاتورة للتنبؤ بمبلغ الإكرامية. ولكن، احتوت بيانات الإكراميات على بيانات اسمية، مثل أيام الأسبوع ونوع الوجبة. هندسة الخصائص تسمح لنا بتحويل البيانات الاسمية إلى كمية لاستخدامها في الانحدار الخطي.
تسمح لنا هندسة الخصائص أيضاً باستخدام نموذج الانحدار الخطي لإجراء انحدار متعدد الحدود عن طريق إنشاء متغيرات جديده في بياناتنا.
بيانات وول مارت
في عام 2014، قامت ول مارت بنشر بعض بيانات بيعها كجزء من مسابقة للتنبؤ بالمبيعات الأسبوعية في فروعها. أخذنا جزء من هذه البيانات واستخدمناها في المثال التالي:
وول مارت Walmart هي إحدى أكبر متاجر التجزئة والمنتجات اليومية في الولايات المتحدة الأمريكية.
لتحميل البيانات walmart.csv اضغط هنا.
import pandas as pd
walmart = pd.read_csv('walmart.csv')
walmart
| MarkDown | Unemployment | Fuel_Price | Temperature | IsHoliday | Weekly_Sales | Date | |
|---|---|---|---|---|---|---|---|
| No Markdown | 8.106 | 2.572 | 42.31 | No | 24924.5 | 05-02-10 | 0 |
| No Markdown | 8.106 | 2.548 | 38.51 | Yes | 46039.49 | 12-02-10 | 1 |
| No Markdown | 8.106 | 2.514 | 39.93 | No | 41595.55 | 19-02-10 | 2 |
| … | … | … | … | … | … | … | … |
| MarkDown2 | 6.573 | 3.601 | 62.99 | No | 22764.01 | 12-10-12 | 140 |
| MarkDown2 | 6.573 | 3.594 | 67.97 | No | 24185.27 | 19-10-12 | 141 |
| MarkDown1 | 6.573 | 3.506 | 69.16 | No | 27390.81 | 26-10-12 | 142 |
143 rows × 7 columns
تحتوي البيانات على عدد من الخصائص المثيرة للإعجاب، إضافة إلى معلومات ما إذا كان الأسبوع يحتوي على إجازة في العمود IsHoliday، ومعدل البطالة في الأسبوع Unemployment وأي من العروض الخاصة التي قدمها المتجر في ذلك الأسبوع MarkDown.
الهدف هو بناء نموذج يتوقع المتغير Weekly_Sales باستخدام باقي المعلومات في جدول البيانات. باستخدام نموذج الانحدار الخطي يمكننا بشكل مباشر استخدام الأعمدة Temperature، Fuel_Price و Unemployment كونها تحتوي على بيانات كمية.
ضبط النموذج باستخدام مكتبة Scikit-learn
في الفصول السابقة تعلمنا كيف نوجد مشتقة دالة التكلفة واستخدام النزول الاشتقاقي لضبط النموذج. لفعل ذلك، كان علينا تعريف دوال في بايثون لبناء النموذج، دالة التكلفة، مشتقة دالة التكلفة، وخوارزمية النزول الاشتقاقي. رغم أهمية ذلك لعرض وفهم المفاهيم في بناء النماذج، في هذا الفصل سنستخدم مكتبة متخصصة بتعلم الآلة اسمها scikit-learn والتي تسمح لنا بضبط النماذج باستخدام أكواد برمجية أقل.
مثلاً، لضبط نموذج انحدار خطي متعدد باستخدام البيانات الكمية في قاعدة بيانات وول مارت، نقوم أولاً ببناء مصفوفة ثنائية الأبعاد باستخدام NumPy تحتوي على المتغيرات المستخدمة لبناء نموذج التنبؤ و مصفوفة أحادية الأبعاد تحتوي على القيم التي نريد التنبؤ عنها:
numerical_columns = ['Temperature', 'Fuel_Price', 'Unemployment']
X = walmart[numerical_columns].to_numpy()
X
array([[ 42.31, 2.57, 8.11],
[ 38.51, 2.55, 8.11],
[ 39.93, 2.51, 8.11],
...,
[ 62.99, 3.6 , 6.57],
[ 67.97, 3.59, 6.57],
[ 69.16, 3.51, 6.57]])
y = walmart['Weekly_Sales'].to_numpy()
y
array([ 24924.5 , 46039.49, 41595.55, ..., 22764.01, 24185.27,
27390.81])
ثم نستدعي كلاس الانحدار الخطي LinearRegression من مكتبة scikit-learn (مزيد من التفاصيل اضغط هنا)، نعرّف بالنموذج، ثم نستدعي دالة الضبط fit باستخدام المتغيرات X للتنبؤ بقيمة y.
لاحظ أننا في السابق احتجنا لإضافة عمود جديد يدوياً يحتوي على القيمة $ 1 $ للمصفوفة X “التحيز” لنقوم بتطبيق الانحدار الخطي. هذه المرة، scikit-learn ستتكفل بفعل ذلك لتختصر علينا الوقت:
from sklearn.linear_model import LinearRegression
simple_classifier = LinearRegression()
simple_classifier.fit(X, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
رائع! عندما نستدعي .fit، مكتبة scikit-learn أوجدت المتغيرات التي تقلل من دالة تكلفة المربعات الصغرى. يمكننا الاطلاع على المتغيرات كالتالي:
simple_classifier.coef_, simple_classifier.intercept_
(array([ -332.22, 1626.63, 1356.87]), 29642.700510138635)
لحساب تكلفة المتوسط التربيعي، يمكننا أن نطلب من المصنف Classifier التنبؤ للقيم المدخلة في X ومقارنة النتيجة مع البيانات الحقيقة في y:
import numpy as np
predictions = simple_classifier.predict(X)
np.mean((predictions - y) ** 2)
74401210.603607252
يظهر أن الخطأ التربيعي المتوسط يبدو مرتفعاً جداً. على الأرجح يكون سبب ذلك هو المتغيرات الثلاثة الكمية التي استخدمناها وارتباطها الضعيف بالمبيعات الأسبوعية.
لدينا متغيران آخران من الممكن أن يكون لهما فائدة في التنبؤ: عمود IsHoliday و MarkDown. مخطط الصندوق في الأسفل يوضح أن الإجازات قد يكون لها ارتباط مع المبيعات الأسبوعية:
import seaborn as sns
sns.pointplot(x='IsHoliday', y='Weekly_Sales', data=walmart);
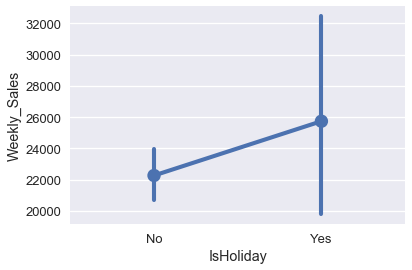
يظهر ان هناك رابط بين الأنواع المختلفة للعروض في العمود MarkDown وبين كمية المبيعات في الأسابيع المختلفة:
import matplotlib.pyplot as plt
markdowns = ['No Markdown', 'MarkDown1', 'MarkDown2', 'MarkDown3', 'MarkDown4', 'MarkDown5']
plt.figure(figsize=(7, 5))
sns.pointplot(x='Weekly_Sales', y='MarkDown', data=walmart, order=markdowns);
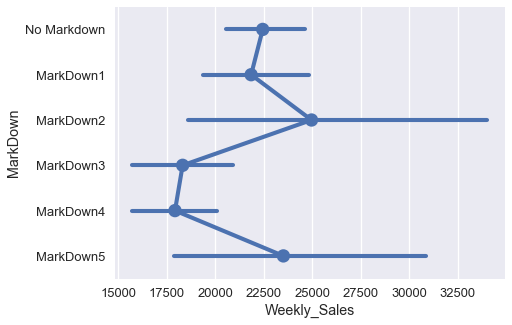
ولكن، كلا الأعمدة IsHoliday و MarkDown هي بيانات أسميه، وليست كمية، لذا لا يمكن أن نستخدمها كما هي الآن في الانحدار.
استخدام One-Hot Encoding
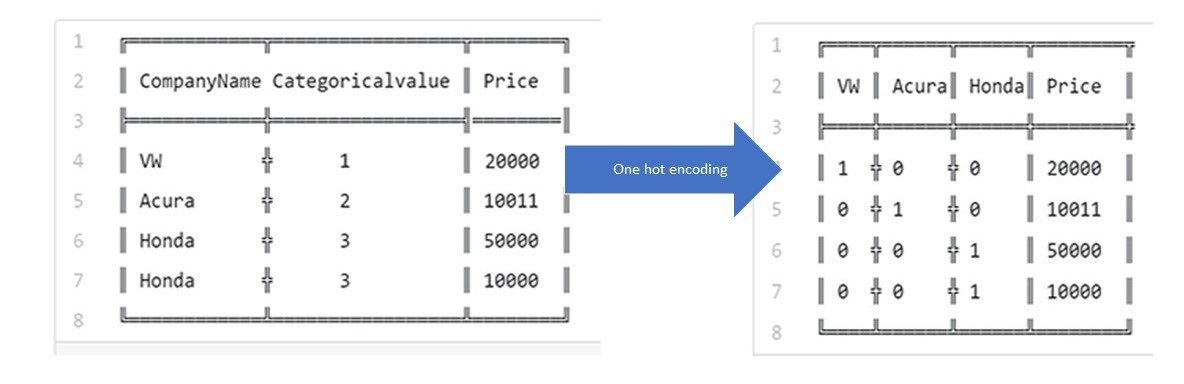
لحسن الحظ، يمكننا أن نستخدم One-Hot Encoding على هذه البيانات الاسمية لتحويلها لكمية. التحويل يتم كالتالي: ننشأ عمود جديد لكل قيمه مختلفة في العمود الأسمي. يحتوي كل عمود على الرقم $ 1 $ إذا كانت العمود هو تلك القيمة الموجودة في العمود الأسمي، وغير ذاك تكون القيمة $ 0 $، مثلاً في العمود MarkDown:
walmart[['MarkDown']]
| MarkDown | |
|---|---|
| No Markdown | 0 |
| No Markdown | 1 |
| No Markdown | 2 |
| … | … |
| MarkDown2 | 140 |
| MarkDown2 | 141 |
| MarkDown1 | 142 |
143 rows × 1 columns
يحتوي العمود على ست قيم مختلفة وهي: No Markdown، MarkDown1، MarkDown2، MarkDown3، MarkDown4، و MarkDown5. نقوم بإنشاء عمود لكل قيمه وينتج لنا ست أعمدة جديده. ثم نقوم بتعبئة كل عمود بصفر أو واحد بنفس الطريقة التي شرحناها مسبقاً.
from sklearn.feature_extraction import DictVectorizer
items = walmart[['MarkDown']].to_dict(orient='records')
encoder = DictVectorizer(sparse=False)
pd.DataFrame(
data=encoder.fit_transform(items),
columns=encoder.feature_names_
)
| MarkDown=No Markdown | MarkDown=MarkDown5 | MarkDown=MarkDown4 | MarkDown=MarkDown3 | MarkDown=MarkDown2 | MarkDown=MarkDown1 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 2 |
| … | … | … | … | … | … | … |
| 0 | 0 | 0 | 0 | 1 | 0 | 140 |
| 0 | 0 | 0 | 0 | 1 | 0 | 141 |
| 0 | 0 | 0 | 0 | 0 | 1 | 142 |
143 rows × 6 columns
لاحظ أن أول سطر في البيانات هي No Markdown، لذا فقط آخر عمود في الجدول الذي تم إنشاءه تحتوي على الرقم $ 1 $. وأيضاً، آخر سطر في البيانات يحتوي على MarkDown1 مما جعل أو عمود يحتوي على $ 1 $.
كل سطر في الجدول يحتوي على عمود واحد لدية الرقم $ 1 $، والبقية ستحتوي على $ 0 $. السم “One-Hot” يعني أن عمود واحد سيكون ذو قيمه (يحتوي على 1).
مثال آخر تم ذكره في الفصل السابق:
طريقة One-Hot Encoding في مكتبة Scikit-learn
لنقوم بعملية One-Hot Encoding يمكننا استخدام الكلاس DictVectorizer من مكتبة scikit-learn. لنستخدم هذه الكلاس، نحتاج لتحويل ال DataFrame إلى مصفوفة تحتوي على قواميس. الكلاس DictVectorizer يقوم بشكل تلقائي بعملية One-Hot Encoding للأعمدة الاسمية (والتي يجب أن تكون نصوص) ولا يقوم بتغير أي عمود يحتوي على قيم كمية:
from sklearn.feature_extraction import DictVectorizer
all_columns = ['Temperature', 'Fuel_Price', 'Unemployment', 'IsHoliday',
'MarkDown']
records = walmart[all_columns].to_dict(orient='records')
encoder = DictVectorizer(sparse=False)
encoded_X = encoder.fit_transform(records)
encoded_X
array([[ 2.57, 1. , 0. , ..., 1. , 42.31, 8.11],
[ 2.55, 0. , 1. , ..., 1. , 38.51, 8.11],
[ 2.51, 1. , 0. , ..., 1. , 39.93, 8.11],
...,
[ 3.6 , 1. , 0. , ..., 0. , 62.99, 6.57],
[ 3.59, 1. , 0. , ..., 0. , 67.97, 6.57],
[ 3.51, 1. , 0. , ..., 0. , 69.16, 6.57]])
لتتبين لك الفكرة والشكل الجديد للبيانات، يمكننا عرضها مع أسماء الأعمدة:
pd.DataFrame(data=encoded_X, columns=encoder.feature_names_)
| Unemployment | Temperature | MarkDown=No Markdown | MarkDown=MarkDown5 | … | MarkDown=MarkDown1 | IsHoliday=Yes | IsHoliday=No | Fuel_Price | |
|---|---|---|---|---|---|---|---|---|---|
| 8.106 | 42.31 | 1 | 0 | … | 0 | 0 | 1 | 2.572 | 0 |
| 8.106 | 38.51 | 1 | 0 | … | 0 | 1 | 0 | 2.548 | 1 |
| 8.106 | 39.93 | 1 | 0 | … | 0 | 0 | 1 | 2.514 | 2 |
| … | … | … | … | … | … | … | … | … | … |
| 6.573 | 62.99 | 0 | 0 | … | 0 | 0 | 1 | 3.601 | 140 |
| 6.573 | 67.97 | 0 | 0 | … | 0 | 0 | 1 | 3.594 | 141 |
| 6.573 | 69.16 | 0 | 0 | … | 1 | 0 | 1 | 3.506 | 142 |
143 rows × 11 columns
الأعمدة الكمية Fuel price، Temperature و Unemployment بقيت كما هي كأرقام. الأعمدة الاسمية IsHoliday و MarkDown تم تطبيق ال One-Hot Encoding عليها. عندما نستخدم المصفوفة الجديدة للبيانات لضبط نموذج الانحدار الخطي، سنقوم بإيجاد متغير جديد لكل عمود في البيانات. بما أن المصفوفة تحتوي على 11 أعمدة، النموذج سيتنبأ ب 12 متغير بما أننا أضفنا متغير إضافي للتحيز.
ضبط النموذج باستخدام البيانات المُعدلة
يمكننا الآن استخدام encoded_X في نموذج الانحدار الخطي:
clf = LinearRegression()
clf.fit(encoded_X, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
كما ذكرنا مُسبقاً، ستكون النتيجة مكونة من 12 قيمه لكل عمود:
clf.coef_, clf.intercept_
(array([ 1622.11, -2.04, 2.04, 962.91, 1805.06, -1748.48,
-2336.8 , 215.06, 1102.25, -330.91, 1205.56]), 29723.135729284979)
يمكننا مقارنة نتائج التوقع بين كلا النماذج لنرى إذا كان هناك فرق كبير بينهما:
walmart[['Weekly_Sales']].assign(
pred_numeric=simple_classifier.predict(X),
pred_both=clf.predict(encoded_X)
)
| pred_both | pred_numeric | Weekly_Sales | |
|---|---|---|---|
| 30766.79021 | 30768.87804 | 24924.5 | 0 |
| 31989.4104 | 31992.2795 | 46039.49 | 1 |
| 31460.28001 | 31465.22016 | 41595.55 | 2 |
| … | … | … | … |
| 24447.34898 | 23492.26265 | 22764.01 | 140 |
| 22788.04955 | 21826.41479 | 24185.27 | 141 |
| 21409.36746 | 21287.92854 | 27390.81 | 142 |
143 rows × 3 columns
في الجدول السابق، العمود
pred_numericيمثل نتائج النموذجsimple_classifierوالذي استخدم فقط الأعمدة الكمية في بياناتنا. بينماpred_bothاستخدم كامل الأعمدة.
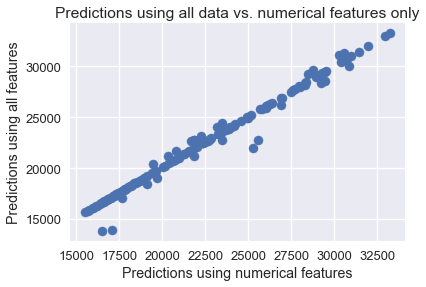
نلاحظ أن نتائج التوقع قريبه بين النموذجان. يمكن رسم مخطط التشتت لكلا الأعمدة لتوضيح ذلك:
plt.scatter(simple_classifier.predict(X), clf.predict(encoded_X))
plt.title('Predictions using all data vs. numerical features only')
plt.xlabel('Predictions using numerical features')
plt.ylabel('Predictions using all features');
تقييم النموذج
لماذا ظهرت لنا النتائج هكذا؟ يمكننا عرض المتغيرات التي اعتمدها النموذجان. الجدول في الأسفل يوضح الأوزان المناسبة التي تعلم عليها المُصنف باستخدام الأعمدة الكمية فقط:
def clf_params(names, clf):
weights = (
np.append(clf.coef_, clf.intercept_)
)
return pd.DataFrame(weights, names + ['Intercept'])
clf_params(numerical_columns, simple_classifier)
| 0 | |
|---|---|
| -332.22118 | Temperature |
| 1626.625604 | Fuel_Price |
| 1356.868319 | Unemployment |
| 29642.70051 | Intercept |
الجدول في الأسفل يوضح الأوزان المناسبة التي تعلم عليها المُصنف بعد تطبيق One-Hot Encoding على البيانات:
pd.options.display.max_rows = 13
display(clf_params(encoder.feature_names_, clf))
pd.options.display.max_rows = 7
| 0 | |
|---|---|
| 1622.106239 | Fuel_Price |
| -2.041451 | IsHoliday=No |
| 2.041451 | IsHoliday=Yes |
| 962.908849 | MarkDown=MarkDown1 |
| 1805.059613 | MarkDown=MarkDown2 |
| -1748.475046 | MarkDown=MarkDown3 |
| -2336.799791 | MarkDown=MarkDown4 |
| 215.060616 | MarkDown=MarkDown5 |
| 1102.24576 | MarkDown=No Markdown |
| -330.912587 | Temperature |
| 1205.564331 | Unemployment |
| 29723.13573 | Intercept |
في الكود البرمجي السابق، عرف الكاتب دالة
clf_paramsوالتي تستقبل اسم الأعمدة و النموذج، وتنتج لنا DataFrame بقيم الأوزان لكل عمود. العمودInterceptهنا هو الانحياز.
نلاحظ أنه حتى بعد ضبط نموذج الانحدار الخطي باستخدام One-Hot Encoding الأوزان للأعمدة Fuel price، Temperature و Unemployment مشابهة بشكل كبير للبيانات قبل التعديل. جميع قيم الأوزان قليلة مقارنة بالانحياز Intercept، يشير ذلك إلى أن أكثر المتغيرات لا يزال ارتباطها قليل مع القيم الحقيقة للمبيعات. في الحقيقة، وزن العمود IsHoliday في النموذج قليل جداً مما يجعله لا يشكل فرقاً في التنبؤ. على الرغم أن بعض الأوزان في العمود MarkDown تبدو مرتفعه جداً، الكثير منها لم يظهر إلا قليلاً:
walmart['MarkDown'].value_counts()
No Markdown 92
MarkDown1 25
MarkDown2 13
MarkDown5 9
MarkDown4 2
MarkDown3 2
Name: MarkDown, dtype: int64
يشير ذلك أننا نحتاج لجمع المزيد من البيانات ليكون للعمود MarkDown تأثير على قيمة المبيعات. ( في الحقيقة، البيانات هنا هي جزء صغير من البيانات الحقيقة الكاملة والتي نشرتها وول مارت. سيكون تدريباً مناسباً لو قمت بتجربة ضبط النموذج وتدريبه على كامل البيانات بدلاً من جزء بسيط منها).
ملخص بيانات وول مارت
تعلمنا كيف نستخدم One-Hot Encoding، طريقة مناسبة لتطبيق الانحدار الخطي على البيانات الاسمية. على الرغم أن في هذا المثال تطبيق ذلك لم يؤثر كثيراً على النموذج، عملياً تستخدم هذه الطريقة بشكل كبير للتعامل مع البيانات الاسمية. One-Hot Encoding تعتبر أحد المبادئ العامة في هندسة الخصائص، تأخذ مصفوفة/عمود من البيانات وتحولها إلى مصفوفات/أعمدة ذات أهمية أكبر.
التنبؤ بتقييم الآيس كريم
لنفترض أننا نريد صناعة نكهة جديده وتكسب شهره من الآيس كريم. نحن مهتمون بحل مشكلة الانحدار التالية: بناءًا على نسبة حلاوة نكهة الآيس كريم، نريد التنبؤ عن التقييم العام للآيس كريم من 7.
لتحميل البيانات icecream.csv اضغط هنا.
ice = pd.read_csv('icecream.csv')
ice
| overall | sweetness | |
|---|---|---|
| 3.9 | 4.1 | 0 |
| 5.4 | 6.9 | 1 |
| 5.8 | 8.3 | 2 |
| … | … | … |
| 5.9 | 11 | 6 |
| 5.5 | 11.7 | 7 |
| 5.4 | 11.9 | 8 |
9 rows × 2 columns
على الرغم من توقعنا أن نكهات الآيس كريم التي لا تعتبر ذات حلاوة عاليه ستحصل على تقييم أقل، نتوقع أيضاً أن النكهات ذات الحلاوة العالية ستحصل أيضاً على تقييم أقل. يتبين لنا ذلك في رسمه مخطط التشتت للتقييم مقارنة بحلاوة الآيس كريم:
sns.lmplot(x='sweetness', y='overall', data=ice, fit_reg=False)
plt.title('Overall taste rating vs. sweetness');
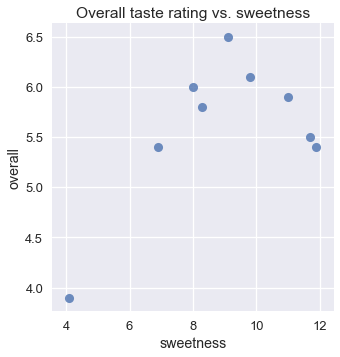
للأسف، لا يمكن للنموذج الخطي وحدة من التعامل مع الزيادة والنقصان الواضحة في الرسم البياني؛ في النموذج الخطي، التقييم يزداد أو ينقص مع حلاوة الآيس كريم. نرى أن استخدام النموذج الخطي يظهر لنا نتائج سيئة.
sns.lmplot(x='sweetness', y='overall', data=ice)
plt.title('Overall taste rating vs. sweetness');
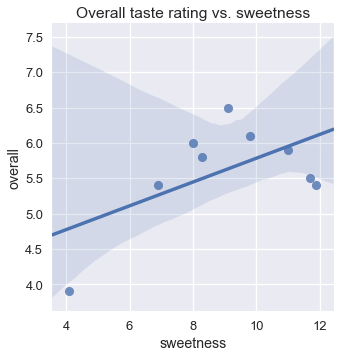
طريقة مفيدة لحل مثل هذه المشاكل هي باستخدام المنحنيات متعددة الحدود بدلاً من الخط. مثل هذه المنحنيات تساعدنا على بناء نموذج يتعامل مع الزيادة في التقييم حتى الوصول لنقطة معينة من الحلاوة، ثم النقص بالتقييم مع الزيادة في الحلاوة.
باستخدام تقنيات معينة في هندسة الخصائص، يمكننا أن ننشأ أعمدة جديده في البيانات لتساعدنا على استخدام النموذج الخطي للانحدار متعدد الخطوط.
خصائص متعددة الحدود
لنتذكر أن في الانحدار الخطي نقوم بضبط وزن واحد لكل عمود في المصفوفة $ X $. في هذه الحالة، في المصفوفة $ X $ سيكون لدينا عامودان: عمود يحتوي على الرقم 1 و آخر يحتوي على مستوى حلاوة الآيس كريم:
from sklearn.preprocessing import PolynomialFeatures
first_X = PolynomialFeatures(degree=1).fit_transform(ice[['sweetness']])
pd.DataFrame(data=first_X, columns=['bias', 'sweetness'])
| sweetness | bias | |
|---|---|---|
| 4.1 | 1.0 | 0 |
| 6.9 | 1.0 | 1 |
| 8.3 | 1.0 | 2 |
| … | … | … |
| 11 | 1.0 | 6 |
| 11.7 | 1.0 | 7 |
| 11.9 | 1.0 | 8 |
9 rows × 2 columns
بذلك يمكننا تعريف النموذج كالتالي:
\[f_\hat{\theta} (x) = \hat{\theta_0} + \hat{\theta_1} \cdot \text{sweetness}\]يمكننا إنشاء عمود جديد في $ X $ يحتوي على تربيع العمود sweetness:
second_X = PolynomialFeatures(degree=2).fit_transform(ice[['sweetness']])
pd.DataFrame(data=second_X, columns=['bias', 'sweetness', 'sweetness^2'])
| sweetness^2 | sweetness | bias | |
|---|---|---|---|
| 16.81 | 4.1 | 1.0 | 0 |
| 47.61 | 6.9 | 1.0 | 1 |
| 68.89 | 8.3 | 1.0 | 2 |
| … | … | … | … |
| 121 | 11 | 1.0 | 6 |
| 136.89 | 11.7 | 1.0 | 7 |
| 141.61 | 11.9 | 1.0 | 8 |
9 rows × 3 columns
بما أن النموذج سيتعلم الحصول على وزن واحد لكل عمود في المصفوفة المعطاة له، سيكون نموذجنا كالتالي:
\[f_\hat{\theta} (x) = \hat{\theta_0} + \hat{\theta_1} \cdot \text{sweetness} + \hat{\theta_2} \cdot \text{sweetness}^2\]يمكن لنموذجنا الآن أن يضبط متعددة الخطوط من الدرجة الثانية. يمكننا أن نضبط درجات أعلى من متعددة الخطوط بإضافة أعمدة جديده لحلاوة الآيس كريم $ \text{sweetness}^3 $ ، $ \text{sweetness}^4 $ وهكذا.
لاحظ أن هذا النموذج لا يزال نموذج خطي، لأن مُعلماته خطية، كل $ \hat{\theta_i} $ هي قيمة عددية من الدرجة الأولى. ولكن، النموذج متعدد الحدود بخصائصه لأن البيانات تحتوي على عمود متعدد الحدود تم إيجاده من عمود آخر.
الانحدار متعدد الحدود
لتطبيق الانحدار متعدد الحدود، نستخدم نموذج خطي مع خصائص متعددة الحدود. لذا، نقوم بإستدعاء النموذج LinearRegression و PolynomialFeatures من مكتبة scikit-learn.
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
تحتوي المصفوفة الأصليه $ X $ على القيم التاليه. تذكر أن البيانات الأصلية لا تحتوي على الرقم التسلسلي ومسمى العواميد، المصفوفة الأصلية $ X $ تحتوي على الأرقام فقط:
ice[['sweetness']]
| sweetness | |
|---|---|
| 4.1 | 0 |
| 6.9 | 1 |
| 8.3 | 2 |
| … | … |
| 11 | 6 |
| 11.7 | 7 |
| 11.9 | 8 |
9 rows × 1 columns
نستخدم أولاً الكلاس PolynomialFeatures لتحويل البيانات، نضيف الخصائص متعددة الحدود من الدرجة الثانية:
transformer = PolynomialFeatures(degree=2)
X = transformer.fit_transform(ice[['sweetness']])
X
array([[ 1. , 4.1 , 16.81],
[ 1. , 6.9 , 47.61],
[ 1. , 8.3 , 68.89],
...,
[ 1. , 11. , 121. ],
[ 1. , 11.7 , 136.89],
[ 1. , 11.9 , 141.61]])
الآن، نقوم بضبط النموذج الخطي على بيانات هذه المصفوفة:
clf = LinearRegression(fit_intercept=False)
clf.fit(X, ice['overall'])
clf.coef_
array([-1.3 , 1.6 , -0.09])
المتغيرات السابقة تظهر أن لهذه البيانات، أفضل قيمة لضبط النموذج هي:
\[f_\hat{\theta} (x) = -1.3 + 1.6 \cdot \text{sweetness} - 0.09 \cdot \text{sweetness}^2\]الآن، يمكننا مقارنة توقعات هذا النموذج مع البيانات الأصلية:
sns.lmplot(x='sweetness', y='overall', data=ice, fit_reg=False)
xs = np.linspace(3.5, 12.5, 1000).reshape(-1, 1)
ys = clf.predict(transformer.transform(xs))
plt.plot(xs, ys)
plt.title('Degree 2 polynomial fit');
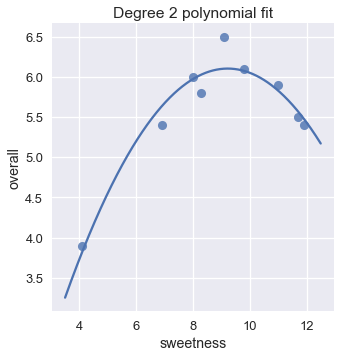
هذا النموذج يظهر أنه أفضل بكثير من النموذج الخطي، يمكننا التأكد أيضاً من أن تكلفة المتوسط التربيعي لمتعددة الحدود من الدرجة الثانية أقل بكثير من التكلفة للخطي:
y = ice['overall']
pred_linear = (
LinearRegression(fit_intercept=False).fit(first_X, y).predict(first_X)
)
pred_quad = clf.predict(X)
# دالة لحاسب المتوسط
def mse_cost(pred, y):
return np.mean((pred - y) ** 2)
print(f'MSE cost for linear reg: {mse_cost(pred_linear, y):.3f}')
print(f'MSE cost for deg 2 poly reg: {mse_cost(pred_quad, y):.3f}')
MSE cost for linear reg: 0.323
MSE cost for deg 2 poly reg: 0.032
زيادة الدرجة
كما ذكرنا سابقاً، يمكننا زيادة درجة متعددة الحدود بإضافة المزيد من الخصائص للبيانات. مثلاً، يمكننا بسهولة إنشاء خصائص من الدرجة الخامسة لمتعددة الحدود وستكون كالتالي:
second_X = PolynomialFeatures(degree=5).fit_transform(ice[['sweetness']])
pd.DataFrame(data=second_X,
columns=['bias', 'sweetness', 'sweetness^2', 'sweetness^3',
'sweetness^4', 'sweetness^5'])
| sweetness^5 | sweetness^4 | sweetness^3 | sweetness^2 | sweetness | bias | |
|---|---|---|---|---|---|---|
| 1158.56201 | 282.5761 | 68.921 | 16.81 | 4.1 | 1 | 0 |
| 15640.31349 | 2266.7121 | 328.509 | 47.61 | 6.9 | 1 | 1 |
| 39390.40643 | 4745.8321 | 571.787 | 68.89 | 8.3 | 1 | 2 |
| … | … | … | … | … | … | … |
| 161051 | 14641 | 1331 | 121 | 11 | 1 | 6 |
| 219244.8036 | 18738.8721 | 1601.613 | 136.89 | 11.7 | 1 | 7 |
| 238635.366 | 20053.3921 | 1685.159 | 141.61 | 11.9 | 1 | 8 |
9 rows × 6 columns
ضبط النموذج الخطي باستخدام هذه الخصائص سينتج لنا الانحدار متعدد الحدود من الدرجة الخامسة:
trans_five = PolynomialFeatures(degree=5)
X_five = trans_five.fit_transform(ice[['sweetness']])
clf_five = LinearRegression(fit_intercept=False).fit(X_five, y)
sns.lmplot(x='sweetness', y='overall', data=ice, fit_reg=False)
xs = np.linspace(3.5, 12.5, 1000).reshape(-1, 1)
ys = clf_five.predict(trans_five.transform(xs))
plt.plot(xs, ys)
plt.title('Degree 5 polynomial fit');
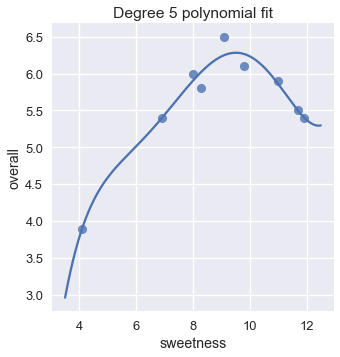
الرسم البياني يظهر أن متعددة الحدود من الدرجة الخامسة نتائجها مشابهة بشكل كبير لمتعددة الحدود من الدرجة الثانية. في الحقيقة، تكلفة المتوسط التربيعي لمتعددة الحدود ذات الدرجة الخامسة بلغت نصف تكلفة المتوسط التربيعي لمتعددة الحدود من الدرجة الثانية:
pred_five = clf_five.predict(X_five)
print(f'MSE cost for linear reg: {mse_cost(pred_linear, y):.3f}')
print(f'MSE cost for deg 2 poly reg: {mse_cost(pred_quad, y):.3f}')
print(f'MSE cost for deg 5 poly reg: {mse_cost(pred_five, y):.3f}')
MSE cost for linear reg: 0.323
MSE cost for deg 2 poly reg: 0.032
MSE cost for deg 5 poly reg: 0.017
يعني ذلك أننا قد نحصل على نتائج أفضل لو قمنا بزايدة الدرجة. لماذا لا نجرب متعددة الحدود من الدرجة العاشرة؟
trans_ten = PolynomialFeatures(degree=10)
X_ten = trans_ten.fit_transform(ice[['sweetness']])
clf_ten = LinearRegression(fit_intercept=False).fit(X_ten, y)
sns.lmplot(x='sweetness', y='overall', data=ice, fit_reg=False)
xs = np.linspace(3.5, 12.5, 1000).reshape(-1, 1)
ys = clf_ten.predict(trans_ten.transform(xs))
plt.plot(xs, ys)
plt.title('Degree 10 polynomial fit')
plt.ylim(3, 7);
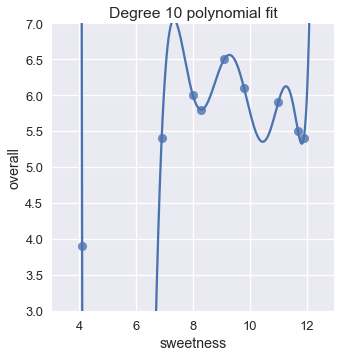
نتائج تكلفة المتوسط التربيعي لجميع نماذج الانحدار التي عرضناها:
pred_ten = clf_ten.predict(X_ten)
print(f'MSE cost for linear reg: {mse_cost(pred_linear, y):.3f}')
print(f'MSE cost for deg 2 poly reg: {mse_cost(pred_quad, y):.3f}')
print(f'MSE cost for deg 5 poly reg: {mse_cost(pred_five, y):.3f}')
print(f'MSE cost for deg 10 poly reg: {mse_cost(pred_ten, y):.3f}')
MSE cost for linear reg: 0.323
MSE cost for deg 2 poly reg: 0.032
MSE cost for deg 5 poly reg: 0.017
MSE cost for deg 10 poly reg: 0.000
متعددة الحدود من الدرجة العاشرة تكلفتها كانت صفر! سنفهم ذلك إذا أمعنا النظر في الرسم البياني؛ تمكنت متعددة الحدود من الدرجة العاشرة من المرور بشكل صحيح على مكان كل نقطة في البيانات.
ولكن، يجب أن تتردد من استخدام الدرجة العاشرة من متعددة الحدود لتوقع تقييم الآيس كريم. متعددة الحدود من الدرجة العاشرة تظهر أنها مضبوطة للبيانات التي لدينا بشكل متقن. إذا حصلنا على بيانات جديده ورسمنا النتائج على مخطط التشتت، نتوقع أن تكون النتائج قريبة من البيانات الأصلية. لو جربنا ذلك على متعددة الحدود من الدرجة العاشرة، فإن النتائج تظهر أسوأ بكثير من متعددة الحدود من الدرجة الثانية:
# انشاء بيانات عشوائية ذات حجم مشابه
# للبيانات الأصليه في المصفوفة ice
# https://numpy.org/doc/stable/reference/random/generated/numpy.random.normal.html
np.random.seed(1)
x_devs = np.random.normal(scale=0.4, size=len(ice))
y_devs = np.random.normal(scale=0.4, size=len(ice))
plt.figure(figsize=(10, 5))
# الدرجة 10 على البيانات الجديده
plt.subplot(121)
ys = clf_ten.predict(trans_ten.transform(xs))
plt.plot(xs, ys)
plt.scatter(ice['sweetness'] + x_devs,
ice['overall'] + y_devs,
c='g')
plt.title('Degree 10 poly, second set of data')
plt.ylim(3, 7);
# الدرجة 2 على البيانات الجديده
plt.subplot(122)
ys = clf.predict(transformer.transform(xs))
plt.plot(xs, ys)
plt.scatter(ice['sweetness'] + x_devs,
ice['overall'] + y_devs,
c='g')
plt.title('Degree 2 poly, second set of data')
plt.ylim(3, 7);
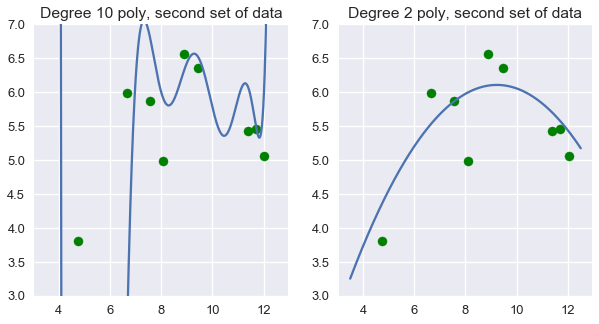
نرى في هذه الحالة، أن متعددة الحدود من الدرجة الثانية حصلت على نتائج أفضل من النموذج دون تغير في الخصائص و متعددة الحدود من الدرجة العاشرة.
ذلك يجعلنا نتسائل: بشكل عام، متى نحدد الضبط المناسب لدرجة متعددة الحدود؟ على الرغم من ترددنا من استخدام التكلفة على بيانات التدريب لإختيار أفضل متعددة الحدود، رأينا أن استخدام التكلفة قد يجعلنا نختار نماذج معقدة جداً. بدلاً من ذلك، نريد تقييم النموذج على بيانات لم تستخدم في ضبط متغيراته.
ملخص التنبؤ بتقييم الآيس كريم
في هذا الجزء، تعرفنا على طريقة أخرى لهندسة الخصائص: إضافة خصائص متعددة الحدود للبيانات من أجل تطبيق الانحدار متعدد الحدود. كما في One-Hot Encoding، إضافة خصائص متعددة الحدود يسمح لنا باستخدام نموذج الانحدار الخطي بشكل فعال على أنواع متعددة من البيانات.
رأينا أيضاً مشكلة أساسية تواجهنا عندما نقوم بهندسة الخصائص. إضافة الكثير من الخصائص يعطي نموذجنا تكلفة أقل على البيانات الأصلية ولكن عادة ما يعطي نتائج غير صحيحه عند تطبيق النموذج على بيانات جديدة.