مبادئ وتقنيات علم البيانات
ملحق: مراجعة الاستدلال الإحصائي
فهرس الفصل:
مقدمة
هذا الملحق يستعرض الاستدلال باستخدام اختبارات التبادل والتمهيد. تم التحدث عن هذه المواضيع في الفصل 12 و 13 من كتاب داتا 8.
على الرغم أن علماء البيانات يعملون على عينات من البيانات، إلا أننا دائماً مهتمين بالتعميم على المجمع الإحصائي التي أتت منة البيانات. هذا الملحق يتحدث عن طرق إجراء الاستدلال الإحصائي Statistical Inference، طريقة لبناء استنتاجات عن كل المجتمع الإحصائي باستخدام البيانات.
نعتمد في الاستدلال الإحصائي بشكل عام على طريقتين: اختبار الفرضيات ومجالات الثقة. في الماضي القريب، اعتمدت هذه الأساليب بشكل كبير على النظرية العادية، والتي هي فرع من الإحصائيات التي تتطلب افتراضيات أساسية عن المجتمع الإحصائي. اليوم، التطور السريع والذي وفر حوسبة قوية أمكن من إيجاد طرق جديدة من الأساليب والتي تعتمد على إعادة التشكيل Resampling والتي تعمم على أنواع كثيره من المجتمعات الإحصائية.
اختبار الفرضيات و مجال الثقة
سيكون هذا الملحق مراجعة بسيطة لاختبار الفرضيات باستخدام التمهيد واختبارات التبادل. نتوقع معرفة بهذه العناوين كونها تم التحدث بشكل كبير عنها في كتاب التفكير الحسابي والاستنتاجي، الكتاب الخاص بمادة داتا 8. للحصول على معلومات وشرح أكثر عن المواضيع التي سيتم شرحها هنا، أطلع على الفصل 11، 12 و 13 من كتاب التفكير الحسابي والاستنتاجي.
اختبارات الفرضية
عند تطبيق مفاهيم علم البيانات في مختلف المجالات، عادة ما نواجه أسئلة عامة. مثلاً، هل شرب القهوة يسبب حرمان النوم؟ هل تتسبب السيارات ذاتية القيادة بحوادث أكثر من السيارات غير ذاتية القيادة؟ هل الدواء X يساعد على علاج الالتهابات الرئوية؟ للمساعدة في الإجابة على هذه الأسئلة، نستخدم اختبارات الفرضية لإيجاد نتائج علمية بناءًا على الأدلة والبيانات التي اطلعنا عليها.
بما أن عملية جمع البيانات عادة ما تحتوي على خطوات غير دقيقة، عادة ما نكون غير متأكدين من الانماط الموجودة في تلك البيانات إن كانت بسبب التشويش أو بسبب بيانات حقيقة عن الالتهاب الرئوي. تساعدنا اختبارات الفرضية على تحديد ما إذا كان النمط في البيانات حدث بسبب التقلبات العشوائية في طريقة جمعنا للبيانات.
سنبدأ بمثال لاستكشاف اختبارات الفرضية. الجدول baby يحتوي على بيانات أوزان الأطفال وقت الولادة. تم تسجيل وزن المواليد بالأونصة وما إذا كانت الأم تدخن أثناء حملها:
لتحميل البيانات baby.csv اضغط هنا.
import pandas as pd
import numpy as np
baby = pd.read_csv('baby.csv')
baby = baby.loc[:, ["Birth Weight", "Maternal Smoker"]]
baby
| Maternal Smoker | Birth Weight | |
|---|---|---|
| FALSE | 120 | 0 |
| FALSE | 113 | 1 |
| TRUE | 128 | 2 |
| … | … | … |
| TRUE | 130 | 1171 |
| FALSE | 125 | 1172 |
| FALSE | 117 | 1173 |
1174 rows × 2 columns
التصميم
نريد أن نرى ما إذا كان تدخين الأم له علاقة بوزن المولود. لإعداد الاختبار لفرضيتنا، يمكننا تمثيل وجهتي النظر العامة كالتالي:
-
فرضية العدم Null hypothesis: في المجتمع الإحصائي، يكون التوزيع للبيانات لأوزان المواليد للأمهات غير المدخنات مساوي للتوزيع لأوزان المواليد من الأمهات المدخنات. الفرق الذي يحدث في البيانات كان بالصدفة.
-
الفرضية البديلة Alternative hypothesis: في المجتمع الإحصائي، متوسط الوزن أثناء الولادة للمواليد من الأمهات المدخنات كان أقل من المواليد من أمهات غير مدخنات.
هدفنا الرئيسي هو اتخاذ قرار بين هذه الفرضيات. نقطة مهمة يجب الانتباه لها وهي أننا أوجدنا هذه الفرضيات بناءًا على المتغيرات Parameters من البيانات وليس من تجاربنا. مثلاً، يجب ألا نقوم ببناء فرضية العدم مثل “وزن مواليد الأمهات المدخنات سيكون مساوي لوزن مواليد الأمهات غير المدخنات”، نظرًا لوجود تبيان بشكل طبيعي في النتائج.
تؤكد فرضية العدم أنه إذا كانت النتائج تظهر عكس ما توقعته الفرضية، فإن ذلك الفرق كان بالصدفة. وبشكل غير رسمي، تقول الفرضية البديلة إن الفرق والاختلاف التي أطلعت عليه “حقيقي”.
يجب أن نلقي نظرة أكثر على شكل فرضيتنا البديلة. في الوضع الحالي، لاحظ أننا سنرفض فرضية العدم إذا كان وزن المواليد من الأمهات المدخنات أقل بشكل واضح وكبير من أوزان المواليد من الأمهات غير المدخنات. بمعنى آخر، الفرضية البديلة تشمل / تدعم جانب واحد من التوزيع. نطلق على ذلك الفرضية البديلة من جانب واحد One-sided Alternative Hypothesis. بشكل عام، نستخدم هذا النوع من الفرضيات البديلة إذا كان لدينا سبب مقنع بأنه لا يمكن أن نرى متوسط وزن لمواليد من أمهات مدخنات أعلى.
لرسم البيانات، قمنا بإنشاء مدرج تكراري لوزن المواليد من الأمهات المدخنات وغير المدخنات:
import matplotlib.pyplot as plt
plt.figure(figsize=(9, 6))
smokers_hist = (baby.loc[baby["Maternal Smoker"], "Birth Weight"]
.hist(density=True, alpha=0.8, label="Maternal Smoker"))
non_smokers_hist = (baby.loc[~baby["Maternal Smoker"], "Birth Weight"]
.hist(density=True, alpha=0.8, label="Not Maternal Smoker"))
smokers_hist.set_xlabel("Baby Birth Weights")
smokers_hist.set_ylabel("Proportion per Unit")
smokers_hist.set_title("Distribution of Birth Weights")
plt.legend()
plt.show()
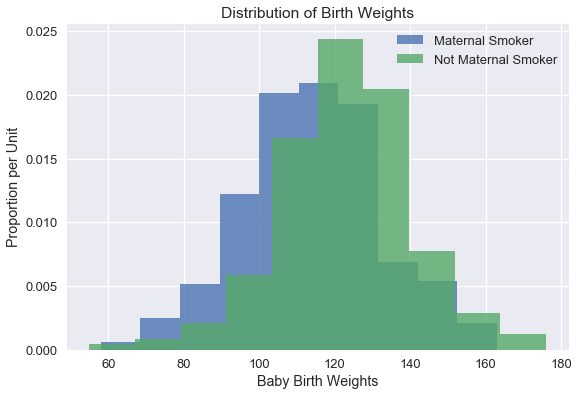
يبدو أن متوسط وزن المواليد من الأمهات المدخنات أقل من وزن المواليد للأمهات غير المدخنات. هل هذا الاختلاف حدث بشكل عشوائي؟ نحاول الإجابة على هذا السؤال باستخدام اختبار الفرضية.
لإجراء اختبار فرضية، نفترض أن نموذج معين يقوم بتوليد البيانات؛ ثم نسأل أنفسنا، ما هي فرصة أن نرى نتائج متطرفة مثل التي رأيناها؟ إذا كانت فرصة مشاهدة تلك النتائج ضئيلة جداً، فقد لا يكون النموذج الذي افترضناه هو النموذج المثالي.
بشكل خاص، نفترض أن فرضية العدم و نموذج إحتماليتها، نموذج العدم Null Model، صحيحان. بمعنى آخر، نفترض أن فرضية العدم صحيحة ونركز على القيمة الإحصائية فيها. نموذج الصدفة يقول انه لا يوجد هناك أي فرق؛ توزيع العينات في الرسم البياني مختلفة فقط بمحض الصدفة.
اختبار الإحصائية
في مثالنا، نفترض أن تدخين الأمهات لا يؤثر على وزن المواليد (وأن أي فرق نطلع عليه حدث بالصدفة). من أجل الاختيار بين فرضياتنا، سنستخدم الفرق بين المجموعتين وتكون اختبار الإحصائية Test Statistic. اختبار الإحصائية هو:
\[\mu_{\text{smoking}} - \mu_{\text{non-smoking}}\]إذاً القيم الصغرى (وهي، القيم السلبية الأعلى) لهذه الإحصائية ستفضل الفرضية البديلة. لنقوم بحساب اختبار الإحصائية للبيانات التي أطلعنا عليها:
nonsmoker = baby.loc[~baby["Maternal Smoker"], "Birth Weight"]
smoker = baby.loc[baby["Maternal Smoker"], "Birth Weight"]
observed_difference = np.mean(smoker) - np.mean(nonsmoker)
observed_difference
-9.266142572024918
إذا لم يكن هناك أي فرق بين التوزيعين في المجتمع الإحصائي، فإذا كانت الأم مدخنة أو غير مدخنة لن يؤثر على متوسط وزن المولود. بمعنى آخر، القيم True و False في عمود تدخين الأم لن تأثر على المتوسط.
لذا، من أجل محاكاة اختبار الإحصائية في فرضية العدم، يمكننا إعادة خلط أوزان المواليد بشكل عشوائي بين الأمهات:
def shuffle(series):
'''
خلط المصفوفة وأعادة تعين الرقم التسلسلي ليتم إضافة القيمة المختلطة لنفس الرقم
'''
return series.sample(frac=1, replace=False).reset_index(drop=True)
baby["Shuffled"] = shuffle(baby["Birth Weight"])
baby
| Shuffled | Maternal Smoker | Birth Weight | |
|---|---|---|---|
| 122 | FALSE | 120 | 0 |
| 167 | FALSE | 113 | 1 |
| 115 | TRUE | 128 | 2 |
| … | … | … | … |
| 116 | TRUE | 130 | 1171 |
| 133 | FALSE | 125 | 1172 |
| 120 | FALSE | 117 | 1173 |
1174 rows × 3 columns
إجراء اختبار التبادل
الاختبارات بناءًا على التبادل العشوائي في البيانات يطلق عليها اختبارات التبادل Permutation Tests، في الكود البرمجي التالي، سنحاكي الاختبار الإحصائي أكثر من مرة ونجمع الفرق في مصفوفة:
differences = np.array([])
repetitions = 5000
for i in np.arange(repetitions):
baby["Shuffled"] = shuffle(baby["Birth Weight"])
# اوجد الفرق بالمتوسط بين مجموعتين عشوائيتين
nonsmoker = baby.loc[~baby["Maternal Smoker"], "Shuffled"]
smoker = baby.loc[baby["Maternal Smoker"], "Shuffled"]
simulated_difference = np.mean(smoker) - np.mean(nonsmoker)
differences = np.append(differences, simulated_difference)
نرسم المدرج التكراري للفرق في المتوسطات
differences_df = pd.DataFrame()
differences_df["differences"] = differences
diff_hist = differences_df.loc[:, "differences"].hist(density=True)
diff_hist.set_xlabel("Birth Weight Difference")
diff_hist.set_ylabel("Proportion per Unit")
diff_hist.set_title("Distribution of Birth Weight Differences");
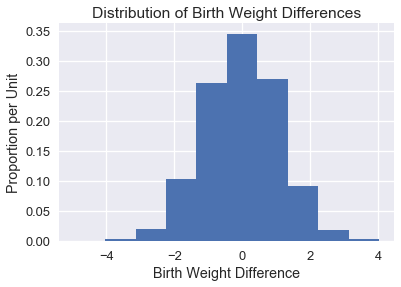
من المنطقي أن يتمحور توزيع الفرق في المتوسطات حول الرقم 9 بما أن المجموعتين يجب أن يكون لها نفس المتوسط في فرضية العدم.
من أجل إيجاد استنتاجات لاختبار الإحصائية، يجب علينا حساب القيمة الاحتمالية p-value. القيمة الاحتمالية التجريبية للاختبار هي نسبة الفرق في البيانات التي حاكيناها التي كانت مساوية أو أقل من فرق البيانات الحقيقية:
p_value = np.count_nonzero(differences <= observed_difference) / repetitions
p_value
0.0
في بداية اختبار الفرضية عادة ما نختار قيمة فصل الأهمية Threshold of Significance (يرمز لها عادة ب $ \alpha $) لقيمة الاحتمالية P-value. إذا كانت قيمة الاحتمالية أقل من قيمة فصل الأهمية، إذا نرفض فرضية العدم. قيم الفصل الأكثر استخدماً هي 0.01 و 0.05، فيها 0.01 تمثل أكثر “تشدد” كوننا نحتاج إلى أدلة أكثر لصالح الفرضية البديلة لرفض فرضية العدم.
في أي من هذه الحالات، نرفض فرضية العدم بما أن قيمة الاحتمالية أقل من قيمة فصل الأهمية.
تمهيد فترات الثقة
يحتاج علماء البيانات في كثير من الأحيان لتقدير متغير المجتمع الإحصائي المجهولة باستخدام عينة عشوائية. على الرغم أننا نفضل أخذ عينات كثيرة من المجتمع الإحصائي لإنشاء توزيع للعينات، غالباً ما نكون مقتصرين على عينة واحدة بسبب الوقت والمال.
لحسن الحظ، العينة العشوائية الكبيرة تبدو مشابهة للمجتمع الإحصائي الأصلي. التمهيد Bootstrap يستخدم ذلك لمحاكاة عينات جديدة عن طريق إعادة أخذ العينات من العينة الأصلية.
لتطبيق التمهيد، نقوم بالخطوات التالية:
- أخذ عينة مع بديلة من العينة الأصلية (والتي هي الآن العينة التي تم تمهيدها). هذه العينات يطلق عليها عينات التمهيد. عادة ما نأخذ الآلاف من عينات التمهيد (~10,000).
- حساب الفائدة الإحصائية لكل عينة تمهيدية. يطلق عليها الإحصائية التمهيدية، والتوزيع التجريبي لهذه الإحصائية التمهيدية هي تقريب لتوزيع العينة في الإحصائية التمهيدية.
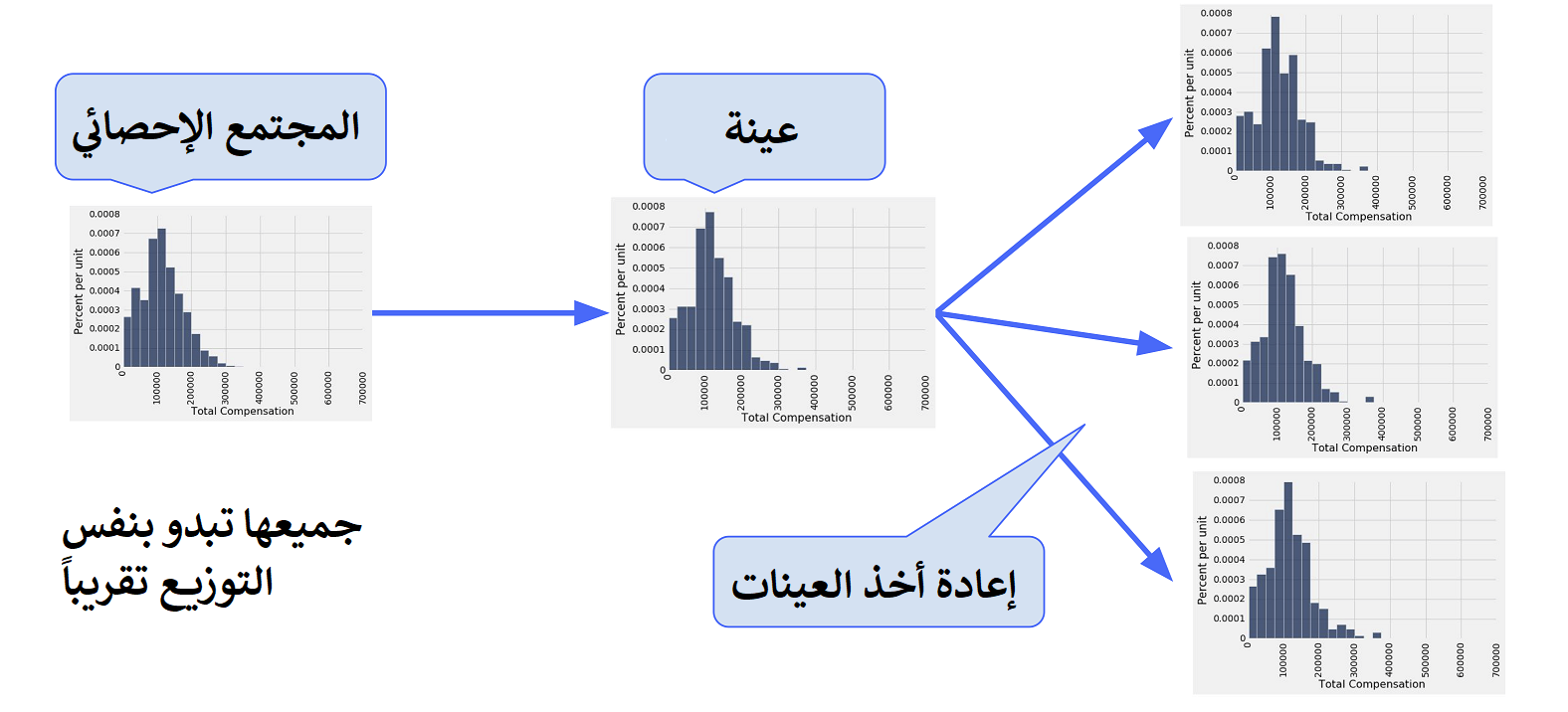
قد نستخدم توزيع عينات التمهيد لإنشاء فترات الثقة والتي نستخدمها لتوقع قيمة متغير المجتمع الإحصائي.
بما أن بيانات الوزن عند الولادة توفر عينة عشوائية حجمها كبير، فقد نعمل على البيانات وكأن الأمهات غير المدخنات يمثلون المجتمع الإحصائي لغير المدخنات. بنفس الطريقة، نقول أن البيانات للأمهات المدخنات يمثلون المجتمع الإحصائي للأمهات المدخنات.
لذا، نعامل العينة الأصلية كتمهيد المجتمع الإحصائي لنتمكن من القيام بخطوات التمهيد:
- نأخذ عينة مع بديل من الأمهات غير المدخنات ونقوم بحساب متوسط وزن المواليد. نأخذ عينة أخرى مع بديل من الأمهات المدخنات ونحسب متوسط وزن المواليد.
- حساب فرق المتوسطات.
- إعادة الخطوات السابقة 10000 مرة، نحصل فيها على 10000 فرق متوسط.
هذه الخطوات تعطينا توزيع تجريبي للعينات للفرق في متوسطات أوزان المواليد:
def resample(sample):
return np.random.choice(sample, size=len(sample))
def bootstrap(sample, stat, replicates):
return np.array([
stat(resample(sample)) for _ in range(replicates)
])
nonsmoker = baby.loc[~baby["Maternal Smoker"], "Birth Weight"]
smoker = baby.loc[baby["Maternal Smoker"], "Birth Weight"]
nonsmoker_means = bootstrap(nonsmoker, np.mean, 10000)
smoker_means = bootstrap(smoker, np.mean, 10000)
mean_differences = smoker_means - nonsmoker_means
mean_differences_df = pd.DataFrame()
mean_differences_df["differences"] = np.array(mean_differences)
mean_diff = mean_differences_df.loc[:, "differences"].hist(density=True)
mean_diff.set_xlabel("Birth Weight Difference")
mean_diff.set_ylabel("Proportion per Unit")
mean_diff.set_title("Distribution of Birth Weight Differences");
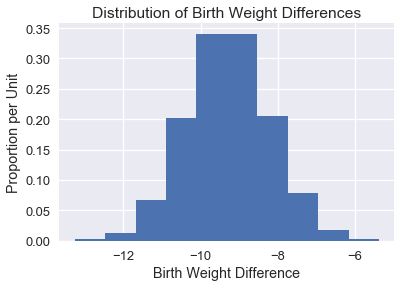
أخيراً، لإيجاد فاصل ثقة بنسبة 95% نوجد النسب المئوية الـ 2.5 و الـ 97.5 في الإحصائية التمهيدية:
(np.percentile(mean_differences, 2.5),
np.percentile(mean_differences, 97.5))
(-11.36909646997882, -7.181670323140913)
فاصل الثقة هذا يسمح لنا بالقول بنسبة ثقة 95% أن الفارق في متوسط الأوزان للمواليد المجتمع الإحصائي بين -11.37 و -7.18 أونصة.
ملخص اختبار الفرضيات و مجال الثقة
في هذا الجزء، راجعنا اختبار الفرضيات باستخدام اختبار التبادل وفاصل الثقة مع التمهيد. للقيام باختبار الفرضية، يجب علينا طرح فرضية العدم والفرضية البديلة، اختيار اختبار الإحصائية المناسب، والقيام بخطوات الاختبار لحساب قيمة الاحتمالية p-value. لإنشاء فاصل ثقة، نختار اختبار إحصاء مناسب، تمهيد العينة الأصلية لإنشاء توزعي تجريبي لاختبار الإحصائية، ونقوم بتحديد الكميات المقابلة لمستوى الثقة الذي لدينا.
اختبار التبادل
هناك عدة حالات نرغب فيها في إجراء اختبار التبادل لتجربة واختبار فرضية والتعرف أكثر على البيانات. اختبار التبادل يعتبر اختبار من النوع الغير معلمي Non-Parametric Test يسمح لنا بإيجاد استنتاجات دون القيام بافتراضات إحصائية والتي تعتبر من نوع الإحصاء المعلمي التقليدي Parametric Test.
أحد الأمثلة الواضحة لاستنتاجات التبادل هو في بيانات تقييم الطلاب للتدريس Student Evaluation of Teaching (SET) بواسطة بورنق، أوتوبوني و ستارك (2016). في هذه الدراسة، 47 طالبًا تم توزيعهم بشكل عشوائي على واحد من أربع أقسام. هناك معلمان يدرسان قسمين؛ إحدى المعلمين ذكر والآخر أنثى. في قسمين، تم التعريف بالمعلمان باستخدام أسمائهم الحقيقية. في الأقسام الأخرى تبادل المعلمان الأسماء.
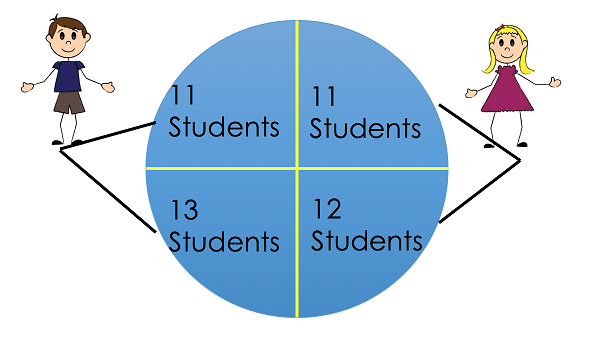
لم يقابل الطلاب المعلمان وجهاً لوجه. كان التفاعل بين الطلاب والمعلمان ألكترونياً. تم تنسيق إعادة الواجبات إلى الطلاب مع الدرجات والملاحظات في نفس الوقت بين المعلمان. أيضاً لدى المعلمان نفس المستوى من الخبرة. في نهاية الفصل، قيّم الطلاب المعلمان في أدائهم لتصحيح الواجبات وإعادتها لهم. أراد المؤلف أن يتحقق إذا كان للجنس تأثير على تقييم الطلاب للتدريس.
الإعداد للتجربة
أجرينا اختبار الفرضية باستخدام فاصل قطع القيمة الاحتمالية p-value يساوي 0.05.
في النموذج Model، لكل مدرس احتمالان للتقييم من كل طالب، واحد لكل جنس متصور لهم (Perceived). لكل طالب فرصة متساوية ليتم تعيينه لتقييم أي من الجنسين في الاختبار (الجنس الحقيقي Gender، الجنس المتصور لهم Perceived Gender) للمعلمان. أخيراً، يقيم الطلاب مدرسيهم بشكل مستقل ومنفصل عن بعضهم.
فرضية العدم Null Hypothesis في هذه التجربة هي الجنس المتصور من الطلاب ليس لدية أي تأثير على تقييم الطلاب للتدريس وأي فرق نلاحظه في التقييم كان بالصدفة. بمعنى آخر، التقييم لكل مدرس يجب ألا يتغير سواء كان يتصور الطلاب أنهم ذكور أو إناث. يعني ذلك أن كل مدرس في الحقيقة سيحصل على تقييم واحد فقط من كل طالب.
الفرضية البديلة Alternative Hypothesis هي أن الجنس المتصور من الطلاب للمدرسين لدية تأثير على تقييم الطلاب للتدريس.
اختبار الإحصائية Test Statistic هو فرق المتوسطات لتقييم الطلاب للمدرسين بتصورهم أنهم ذكور أو إناث. بشكل طبيعي، نتوقع أن تكون النتيجة قريبة من 0 إذا لم يكن للجنس تأثير على التقييم. يمكننا كتابة التالي:
\[\mu_{\text{perceived female}} - \mu_{\text {perceived male}}\]فيها:
\[\begin{split} \begin{aligned} \mu_{\text{perceived female}} &= \frac {\sum_{j=1}^{n_1} x_{1j} + \sum_{j=1}^{n_3} x_{3j}}{ {n_1} + {n_3} } \\ \mu_{\text{perceived male}} &= \frac {\sum_{j=1}^{n_2} x_{2j} + \sum_{j=1}^{n_4} x_{4j}}{ {n_2} + {n_4} } \end{aligned} \end{split}\]وفيها $ n_i $ هي عدد الطلاب في المجموعة $ i $ و $ x_{ij} $ هي تقييم الطالب رقم $ j $ في تلك المجموعة $ i $.
من أجل تحديد ما إذا كان للجنس تأثير على تقييم الطلاب للتدريس، نقوم بإجراء اختبار تبادل لإنشاء توزيع تجريبي لاختبار الإحصاء في فرضية العدم. نقوم بإتباع الخطوات التالية:
- تبديل الجنس المتصور من قبل الطلاب الذين لديهم نفس المعلم. لاحظ أننا نقوم بالخلط من الجزئيين اليسار واليمين من الصورة السابقة.
- حساب الفرق في متوسط تقييم الطلاب في المجموعات التي تم تحديد الجنس فيها كذكر أو أنثى.
- التكرار أكثر من مره لإيجاد توزيع تقريبي للعينات لمتوسط الفرق في التقييم بين المجموعتين.
- استخدام التوزيع التقريبي لتوقع احتمالية إيجاد اختبار إحصاء أكثر تطرفاً مما لاحظناه مسبقاً.
من المهم فهم تبرير اختبار التبادل في هذا المثال. في النموذج العدمي، كل طالب سيعطي مدرسه نفس التقييم أياً كان تصوره للجنس. التعيين العشوائي البسيط يشير أن لكل معلم، جميع تقييماتهم لديها نفس الفرصة أن تظهر أيًا كان تصور الطلاب لهم كذكر أو أنثى. لذا، تبديل الجنس لن يؤثر على التقييم إذا كانت فرضية العدم صحيحة.
البيانات
نبدأ ببيانات الطلاب والجنس التالية. هذه البيانات من مسح إحصائي لـ47 طالب في مسجلين في مادة عبر الإنترنت في إحدى الجامعات الأمريكية:
لتحميل البيانات StudentRatingsData.csv اضغط هنا.
student_eval = (
pd.read_csv('StudentRatingsData.csv')
.loc[:, ["tagender", "taidgender", "prompt"]]
.dropna()
.rename(columns={'tagender': 'actual', 'taidgender': 'perceived'})
)
student_eval[['actual', 'perceived']] = (
student_eval[['actual', 'perceived']]
.replace([0, 1], ['female', 'male'])
)
student_eval
| prompt | perceived | actual | |
|---|---|---|---|
| 4 | male | female | 0 |
| 5 | male | female | 1 |
| 5 | male | female | 2 |
| … | … | … | … |
| 4 | female | male | 43 |
| 2 | female | male | 44 |
| 4 | female | male | 45 |
43 rows × 3 columns
معنى الأعمدة كالتالي:
-
actual: الجنس الحقيقي للمعلم.
-
perceived: الجنس المعطى (المتصور) للطلاب للمعلم.
-
prompt: تقييم الطلاب لأداء المعلمين في تصحيح الواجبات وإعادتها لهم من 1 إلى 5.
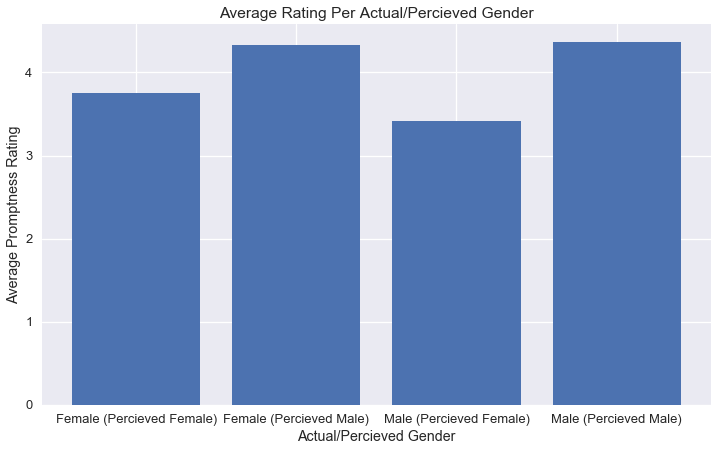
بعد تحليل ورسم البيانات من التجربة، يبدو أن هناك فرق في مجموعات الطلاب، بتصور الطلاب للمعلم كأنثى حصلت على تقييم أقل من تصور الطلاب للمعلم كذكر؛ ولكن، نحتاج اختبار فرضية أساسي لنرى اذا كان الفرق ببساطة بسبب التعيين العشوائي للطلاب:
avg_ratings = (student_eval
.loc[:, ['actual', 'perceived', 'prompt']]
.groupby(['actual', 'perceived'])
.mean()
.rename(columns={'prompt': 'mean prompt'})
)
avg_ratings
| mean prompt | ||
|---|---|---|
| perceived | actual | |
| 3.75 | female | female |
| 4.33 | male | |
| 3.42 | female | male |
| 4.36 | male |
fig, ax = plt.subplots(figsize=(12, 7))
ind = np.arange(4)
plt.bar(ind, avg_ratings["mean prompt"])
ax.set_xticks(ind)
ax.set_xticklabels(['Female (Percieved Female)', 'Female (Percieved Male)', 'Male (Percieved Female)', "Male (Percieved Male)"])
ax.set_ylabel('Average Promptness Rating')
ax.set_xlabel('Actual/Percieved Gender')
ax.set_title('Average Rating Per Actual/Percieved Gender')
plt.show()
تطبيق التجربة
سنقوم بحساب الفرق الواضح في متوسطات التقييم للمعلمين في المجموعات التي تم تحديد جنس المعلم لهم سواء ذكر أو أنثى:
def stat(evals):
# حساب اختبار الإحصاء على الداتا فريم evals
avgs = evals.groupby('perceived').mean()
return avgs.loc['female', 'prompt'] - avgs.loc['male', 'prompt']
observed_difference = stat(student_eval)
observed_difference
-0.79782608695652169
نرى أن الفرق -0.8، في هذه الحالة، متوسط التقييم لمن تم تحديد وإبلاغهم عن جنس المعلم كأنثى اقل بحوالي 1 في المقياس من 1 إلى 5. في هذا المقياس، يظهر أن الفرق كبير جداً. بإجراء اختبار التبادل، يمكن أن نلاحظ فرقاً بهذا الحجم الكبير في نموذج العدم.
الآن، يمكننا تبديل الجنس المصور لكل معلم وحساب اختبار الإحصائية 1000 مره:
def shuffle_column(df, col):
# تنتج لنا الدالة نسخة جديدة من البيانات بعد خلطها
result = df.copy()
result[col] = np.random.choice(df[col], size=len(df[col]))
return result
repetitions = 1000
gender_differences = np.array([
stat(shuffle_column(student_eval, 'perceived'))
for _ in range(repetitions)
])
نرسم توزيع البيانات التقريبي للفرق في التقييم باستخدام التبادل، أظهرنا القيمة التي سبق أن اطلعنا عليها بالخط الأحمر المتقطع:
differences_df = pd.DataFrame()
differences_df["gender_differences"] = gender_differences
gender_hist = differences_df.loc[:, "gender_differences"].hist(density=True)
gender_hist.set_xlabel("Average Gender Difference (Test Statistic)")
gender_hist.set_ylabel("Percent per Unit")
gender_hist.set_title("Distribution of Gender Differences")
plt.axvline(observed_difference, c='r', linestyle='--');
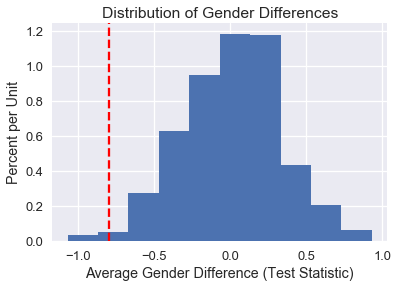
من عملية الحساب التالية، نجد أن القيم الـ1000 التي قمنا بمحاكاتها للبيانات، 18 فقط كان الفرق فيها عالي كالتي رأيناها. لذا، قيمة الاحتمالية p-value أقل من قيمة الفصل 0.05 لذا نرفض فرضية العدم ونفضل الفرضية البديلة:
# متغيرات التوزيع
sample_sd = np.std(gender_differences)
sample_mean = np.mean(gender_differences)
# حساب القيمة الأعلى يميناً
num_sd_away = (sample_mean - observed_difference)/sample_sd
right_extreme_val = sample_mean + (num_sd_away*sample_sd)
# حساب قيمة الإحتمالية p-value
num_extreme_left = np.count_nonzero(gender_differences <= observed_difference)
num_extreme_right = np.count_nonzero(gender_differences >= right_extreme_val)
empirical_P = (num_extreme_left + num_extreme_right) / repetitions
empirical_P
0.018
ملخص اختبار التبادل
من خلال مراجعة اختبار التبادل، رأينا أن تقييم الطلاب للتدريس منحازة ضد المعلمين الإناث بقيمة كبيرة و هامة إحصائياً.
هناك دراسات أخرى اختبرت أيضاً الانحياز في تقييم التدريس. بناءًا على بورنق، أوتوبوني و ستارك (2016)، هناك اختبارات تبادل أخرى تم إجراءها افترضت أن تقييم المعلمين الذكور والإناث هي عينات عشوائية مستقلة من مجتمع إحصائي موزع بشكل طبيعي مع تباينات متساوية؛ هذا النوع من تصميم التجارب لا يتطابق مع فرضية العدم، مما يجعل قيمة الاحتمالية p-value مضللة.
على العكس، بورنق، أوتوبوني و ستارك (2016) إستخدمو اختبار تبادل بناءاً على توزيع عشوائي للطلاب في الأقسام. تذكر عندما قمنا باختبار التبادل، لم نقم بأي فرضيات عن التوزيع في البيانات. في هذه التجربة، لم نفترض أن الطلاب، تقييم الطلاب للتدريس، الدرجات، أو أي من المتغيرات الأخرى تحتوي على عينات عشوائية من أي مجتمع إحصائي، مجتمع إحصائي أقل بكثير و بتوزيع طبيعي.
عند اختبار فرضية، من المهم اختيار تصميم تجربتك وفرضية العدم من أجل الحصول على نتائج موثوقة.