مبادئ وتقنيات علم البيانات
الفصل العاشر: النماذج والتوقعات
فهرس الفصل:
مقدمة
بشكل عام، جميع النماذج خاطئة، ولكن بعضها مفيد.
تحدثنا عن تكوين السؤال، تنظيف البيانات والتحليل الاستكشافي للبيانات، الخطوات الثلاث الأولى في دورة حياة علم البيانات. ورأينا أن التحليل الاستكشافي يظهر علاقات بين القيم في البيانات. كيف يمكننا التحقق إذا كانت هذه العلاقة حقيقة أو لا؟ كيف يمكننا استخدام هذه العلاقات للحصول على توقعات عن المستقبل؟ للإجابة على هذه الأسئلة سنحتاج لأداة رياضية لبناء النماذج والتوقعات.
النموذج Model هو عبارة عن أفضل تمثيل لنظامنا. مثلاً، إذا قمنا برمي كره من الفولاذ من فوق برج بيزا المائل، نموذج بسيط للجاذبية سيتوقع أن الكره سترتطم بالأرض بسرعة 9. 8 م/ث². هذا النموذج سمح لنا بتوقع كم ستأخذ الكرة من وقت للوصول إلى الأرض باستخدام قوانين الحركة.
هذا النموذج للجاذبية يوضح سلوك وأداء نظامنا ولكن فقط في التوقع، لا يقوم بحساب تأثير حركة الهواء، والطفو في الهواء والتأثيرات الأخرى على جاذبية الأجسام أثناء السقوط. بسبب هذه العوامل غير المدروسة، نموذجنا سينتج دائماً توقعات خاطئة! ولكن، النموذج البسيط للجاذبية يعتبر دقيق بشكل كافي في كثير من الأحيان مما يجعله يستخدم ويُعَلم اليوم.
وبنفس الطريقة، كل نموذج نقوم بتعريفه باستخدام بيانات يعتبر تقدير لما هو بالواقع. عندما لا يكون التقدير دقيق جداً، نموذجنا يكون استخدامه مفيد وعملي. وبطبيعة الحال، ستظهر لنا أسئلة أساسيه مثل، كيف نختار النموذج؟ كيف نعرف ما إذا كنا نحتاج نموذج أكثر تعقيداً؟
في الفصول القادمة من هذا الكتاب، سنقوم بتطوير أدوات حسابية لتصميم وندرب النموذج على البيانات. سنقوم أيضا بالتعرف على أدوات استنتاجية تُمكنا من معرفة إذا كان بإمكاننا تعميم نماذجنا.
النماذج
في الولايات المتحدة، الكثير من زوار المطاعم يتركون بعض من المال للنادل أثناء دفعهم لثمن وجباتهم. رغم أنه من المعروف في الولايات المتحدة أن 15% من مجموع الفاتورة يكون كإكرامية، إلا أن بعض المطاعم لديها زبائن مخلصين أكثر من غيرها يقدمون المزيد من المال كإكرامية.
أحد النوادل المهتمين أراد معرفة ما قد يحصل عليه من إكرامية فقام بجمع معلومات عن كافة الطاولات التي خدمها في غضون شهر:
import seaborn as sns
tips = sns.load_dataset('tips')
tips
| size | time | day | smoker | sex | tip | total_bill | |
|---|---|---|---|---|---|---|---|
| 2 | Dinner | Sun | No | Female | 1.01 | 16.99 | 0 |
| 3 | Dinner | Sun | No | Male | 1.66 | 10.34 | 1 |
| 3 | Dinner | Sun | No | Male | 3.5 | 21.01 | 2 |
| … | … | … | … | … | … | … | … |
| 2 | Dinner | Sat | Yes | Male | 2 | 22.67 | 241 |
| 2 | Dinner | Sat | No | Male | 1.75 | 17.82 | 242 |
| 2 | Dinner | Thur | No | Female | 3 | 18.78 | 243 |
244 rows × 7 columns
sns.distplot(tips['tip'], bins=np.arange(0, 10.1, 0.25), rug=True)
plt.xlabel('Tip Amount in Dollars')
plt.ylabel('Proportion per Dollar');
يمكننا رسم مدرج تكراري لمجموع الإكراميات:
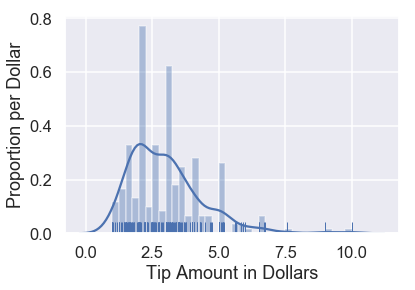
بإمكاننا ملاحظة بعض الأنماط في البيانات. مثلاً، هناك تكرار كبير للقيمة 2$ وغالب الإكراميات من مضاعفات 0.50$.
حالياً، نحن مهتمين بنسبة الإكرامية: قيمة الإكرامية قسمة مجموع الفاتوره. يمكننا إنشاء عمود جديد في ال DataFrame لحفظ هذه القيمه ونعرض توزيع النتائج:
tips['pcttip'] = tips['tip'] / tips['total_bill'] * 100
sns.distplot(tips['pcttip'], rug=True)
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');
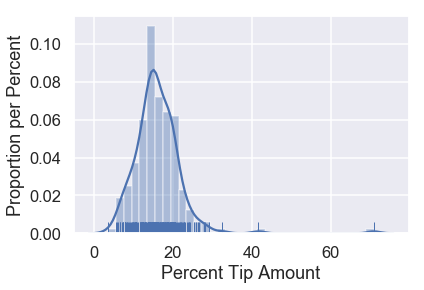
يبدو أن أحد الزبائن ترك للنادل إكرامية قيمتها 70%! ولكن أغلب الإكراميات كان أقل من 30%. لنقرب الرسم البياني إلى ذلك الجزء:
sns.distplot(tips['pcttip'], bins=np.arange(30), rug=True)
plt.xlim(0, 30)
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');
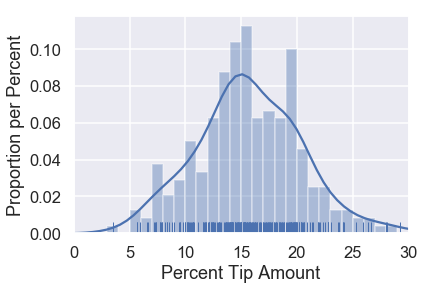
نلاحظ أن توزيع البيانات في الغالب حول 15% مع مجموع تكرار أعلى حول 20%. لنفترض أن نادلنا يريد معرفة كم النسبة التي سيحصل عليها من الزبائن. للإجابة على السؤال، يمكننا بناء نموذج يتوقع كم مبلغ الإكرامية الذي سيحصل عليها النادل.
النموذج البسيط
أحد أمثله على النموذج البسيط هي تجاهل كل البيانات وذكر أنه من المعروف في الولايات المتحدة إعطاء إكرامية بمقدار 15% من مبلغ الفاتورة، بذلك يحصل النادل دائماً على 15% من كل زبون. على الرغم من بساطته، سنستخدم هذه النموذج للتعريف ببعض المتغيرات لاحقاً.
هذا النموذج يفترض أن هناك نسبه وحيده صحيحه لكل الإكراميات التي سيحصل عليها النادل من كل زبائنه. هذه هي معالم المجتمع Population Parameter لنسبة الإكرامية، والتي سنرمز لها بالرمز $ \theta^* $. 📝 📝
بعد فرضيتنا السابقة، نموذجنا سيقول إن توقعه لقيمة $ \theta^* $ هي 15%. سنستخدم الرمز $ \theta $ لوصف التوقع (التنبؤ).
برموز رياضية، فإن نموذجنا يفرض التالي:
\[\theta = 15\]من الواضح أن هذا النموذج يحتوي على مشاكل، إذا كان النموذج صحيح، فإن جميع الزبائن في بياناتنا قد أعطوا إكرامية بقيمة 15%. ولكن، هذا النموذج سيعطي تخميناً معقولاً في كثير من الأحيان. بالأصح، هذا النموذج يعتبر الأكثر فائدة بالنسبة لنا إذا لم يكن لدينا أي معلومات عن النادل والزبائن سوى أنهم في الولايات المتحدة.
بما أن النادل لدينا قام بجمع بيانات، يمكننا استخدام المعلومات التاريخ للإكراميات التي حصل عليها لبناء نموذج يعطي تنبؤ بديل عن 15% المعروفة بين مطاعم الولايات المتحدة.
فائدة دالة الخسارة
عرضنا سابقاً توزيع نسبة الإكراميات في البيانات:
sns.distplot(tips['pcttip'], bins=np.arange(30), rug=True)
plt.xlim(0, 30)
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');

لنفترض أننا نريد مقارنة خيارين ل $ \theta $: $ 10% $ و $ 15% $. يمكننا إظهار هذين الخيارين في رسمنا البياني:
sns.distplot(tips['pcttip'], bins=np.arange(30), rug=True)
plt.axvline(x=10, c='darkblue', linestyle='--', label=r'$ \theta = 10$')
plt.axvline(x=15, c='darkgreen', linestyle='--', label=r'$ \theta = 15$')
plt.legend()
plt.xlim(0, 30)
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');
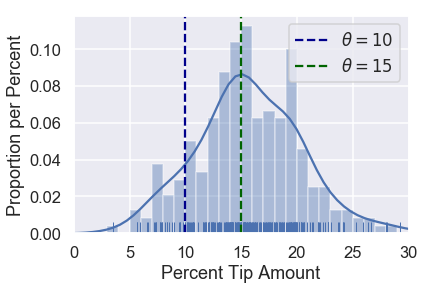
بشكل واضح، يظهر أن اختيار $ \theta = 15 $ يبدو أفضل من $ \theta = 10 $ بِنَاءَا على البيانات. لماذا؟ عندما نلاحظ نقاط البيانات، نرى أن أكثر البيانات كانت أقرب ل 15 من 10.
على الرغم أن $ \theta = 15 $ تبدو خيارًا أفضل، لا نعرف ما إذا كانت هي أفضل من $ \theta = 16 $. لنقوم باختيار دقيق بين مختلف احتمالات $ \theta $، نريد أن نعين لكل $ \theta $ رقم متغير يقيس ما إذا كان مناسب لبياناتنا. يعني ذلك، نحتاج لدالة تأخذ قيمه ل $ \theta $ وقيم من بياناتنا، وتنتج لنا رقماً يمكننا استخدامه لاختيار أفضل القيم ل $ \theta $.
تسمى هذه الدالة بـ دالة الخسارة Loss Function.
دالة الخسارة
لنذكر فرضيتنا السابقة: افترضنا أن هناك نسبه واحدة للإكرامية بين جميع المجتمع $ \theta^* $. نموذجنا يتوقع هذا الرقم؛ سنستخدم $ \theta $ لترميز توقعنا. نريد استخدام البيانات التي جمعناها عن الإكراميات لحساب قيمة $ \theta $.
لتحديد أي قيمه من $ \theta $ هي الصحيحة، عرفنا دالة الخسارة. دالة الخسارة هي دالة رياضية تأخذ توقع ل $ \theta $ ونقطة في بياناتنا $ y_1, y_2, \ldots, y_n $، وتأتي بنتيجة عبارة عن رقم، الخسارة، يقيس مدى دقة $ \theta $ لبياناتنا. برموز رياضية، نريد كتابة الدالة:
\[L(\theta, y_1, y_2, \ldots, y_n) =\ \ldots\]بشكل عام، النتيجة من دالة الخسارة عندما تكون رقماً صغير فإن قيمة $ \theta $ مناسبة وإذا كانت النتيجة من الدالة رقم كبير فإن قيمة $ \theta $ ليست مناسبه. لندرب النموذج، نختار قيم ل $ \theta $ التي تنتج لنا أرقام صغيرة في دالة الخسارة، القيم $ \theta $ التي تقلل من الخسارة. نستخدم الرمز $ \hat{\theta} $ للإشارة لقيم $ \theta $ التي تقلل من دالة الخسارة.
لنفترض مرة أخرى القيم التالية ل $ \theta $: $ \theta = 10 $ و $ \theta = 15 $:
sns.distplot(tips['pcttip'], bins=np.arange(30), rug=True)
plt.axvline(x=10, c='darkblue', linestyle='--', label=r'$ \theta = 10$')
plt.axvline(x=15, c='darkgreen', linestyle='--', label=r'$ \theta = 15$')
plt.legend()
plt.xlim(0, 30)
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');

بما أن $ \theta = 15 $ أقرب للكثير من النقاط، فإن دالة الخسارة من المفترض أن تأتي رقم أقل ل $ \theta = 15 $ ورقم أعلى ل $ \theta = 10 $.
لنستخدم هذه المعلومه لإنشاء دالة الخسارة.
دالة الخسارة الأولى لنا: الخطأ التربيعي المتوسط
نريد ان تكون قيمة $ \theta $ قريبه من الكثير من النقاط في بياناتنا. لذا، نقوم بتعريف دالة خسارة نطبقها على بياناتنا وتأتي بنتائج عاليه ل $ \theta $ إذا كانت بعيدة عن الكثير من البيانات. نبدأ بدالة خسارة بسيطه يطلع عليها الخطأ التربيعي المتوسط Mean Squared Error، هنا فكرتها:
- نختار قيمه ل $ \theta $.
- لكل قيمه في بياناتنا، نأخذ الفرق التربيعي بين تلك القيمة و $ \theta $: $ (y_i - \theta)^2 $. طريقة التربيع هي وسيلة سهله لتحويل القيم السلبية إلى قيم إيجابية. نريد القيام بذلك لأن إذا كانت $ ( y_i = 14 $ فإن كلا القيمتين $ \theta = 10 $ و $ \theta = 18 $ يعتبران بعيدين عن باقي النقاط ويعتبرون قيم غير مناسبة.
- للقيام بعملية الحساب لدالة الخسارة، نأخذ متوسط كل قيمه للفرق التربيعي.
كتابة دالة في بايثون للقيام بعملية حساب دالة الخسارة هذه سهل جداً:
def mse_loss(theta, y_vals):
return np.mean((y_vals - theta) ** 2)
لنرى كيفية أداء هذه الدالة. لنفرض أن لدينا بيانات تحتوي على قيمة واحد فقط، $ y_1 = 14 $. يمكننا تجربة أكثر من قيمه ل $ \theta $ لنرى نتيجة دالة الخسارة لكل قيمه:
# لا يهم معرفة ما يجري في الكود البرمجي التالي، نتيجة الكود هي الصورة في الأسفل
def try_thetas(thetas, y_vals, xlims, loss_fn=mse_loss, figsize=(10, 7), cols=3):
if not isinstance(y_vals, np.ndarray):
y_vals = np.array(y_vals)
rows = int(np.ceil(len(thetas) / cols))
plt.figure(figsize=figsize)
for i, theta in enumerate(thetas):
ax = plt.subplot(rows, cols, i + 1)
sns.rugplot(y_vals, height=0.1, ax=ax)
plt.axvline(theta, linestyle='--',
label=rf'$ \theta = {theta} $')
plt.title(f'Loss = {loss_fn(theta, y_vals):.2f}')
plt.xlim(*xlims)
plt.yticks([])
plt.legend()
plt.tight_layout()
try_thetas(thetas=[11, 12, 13, 14, 15, 16],
y_vals=[14], xlims=(10, 17))
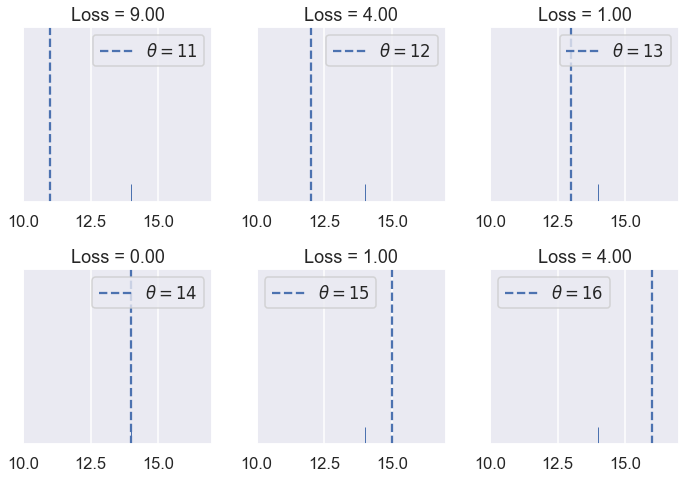
كما توقعنا، قيمة دالة الخسارة أعلى كلما كانت $ \theta $ أبعد من مجمع البيانات وأقل كلما كانت أقرب أو في نفس النقطة. لنرى كيف يتصرف الخطأ التربيعي المتوسط إذا كانت لدينا أكثر من قيمه. لتكن بياناتنا هي القيم التالية: $ [11,12,15,17,18] $
try_thetas(thetas=[12, 13, 14, 15, 16, 17],
y_vals=[11, 12, 15, 17, 18],
xlims=(10.5, 18.5))
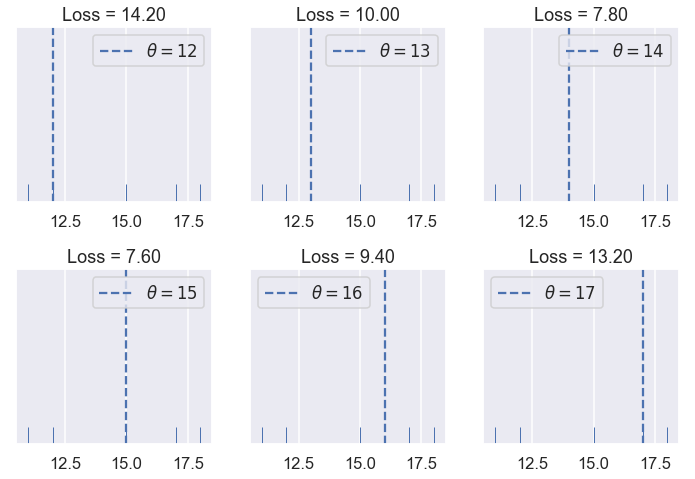
من قيم $ \theta $ السابقة نرى أن $ \theta = 15 $ لديها أقل نتيجة لدالة الخسارة. لكن، يوجد رقم بين 14 و 15 قد يحصل على نتيجة أقل لدالة الخسارة. لنحاول البحث عن تلك القيمه الأفضل ل $ \theta $
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline
import ipywidgets as widgets
from ipywidgets import interact, interactive, fixed, interact_manual
def try_thetas_interact(theta, y_vals, xlims, loss_fn=mse_loss):
if not isinstance(y_vals, np.ndarray):
y_vals = np.array(y_vals)
plt.figure(figsize=(4, 3))
sns.rugplot(y_vals, height=0.1)
plt.axvline(theta, linestyle='--')
plt.xlim(*xlims)
plt.yticks([])
print(f'Loss for theta = {theta}: {loss_fn(theta, y_vals):.2f}')
def mse_interact(theta, y_vals, xlims):
plot = interactive(try_thetas_interact, theta=theta,
y_vals=fixed(y_vals), xlims=fixed(xlims),
loss_fn=fixed(mse_loss))
plot.children[-1].layout.height = '240px'
return plot
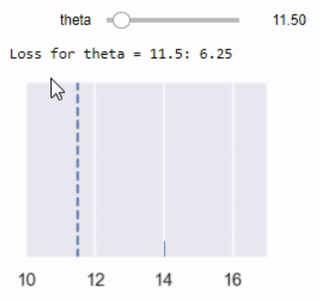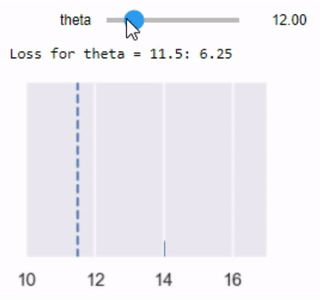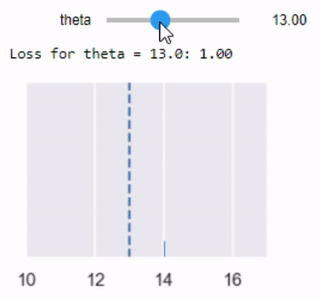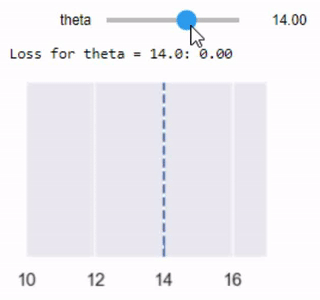
mse_interact(theta=(12, 17, 0.2),
y_vals=[11, 12, 15, 17, 18],
xlims=(10.5, 18.5))
الكود السابق ينتج رسم بياني تفاعلي، يمكننا منه التحكم بقيمة $ \theta $ إلى أن نحصل على نتيجة مناسبة لدالة الخسارة. هذا الطريقة التفاعلية تعمل فقط في Jupyter Notebook لذا إذا أرد تجربتها قم بتشغيل كامل الكود البرمجي مع إضافة المكتبات التي يحتاجها كاملاً في Jupyter Notebook.
نلاحظ ان دالة الخطأ التربيعي المتوسط تؤدي عملها بشكل متقن وذلك بقيامها بمعاقبة قيم $ \theta $ التي تكون بعيدة عن مجموع البيانات. لنرى الآن قيمة دالة الخسارة لبيانات النسبة المئوية للإكرامية، نرسم التوزيع أولا:

لنجرب الآن قيم مختلفة ل $ \theta $:
try_thetas(thetas=np.arange(14.5, 17.1, 0.5),
y_vals=tips['pcttip'],
xlims=(0, 30))
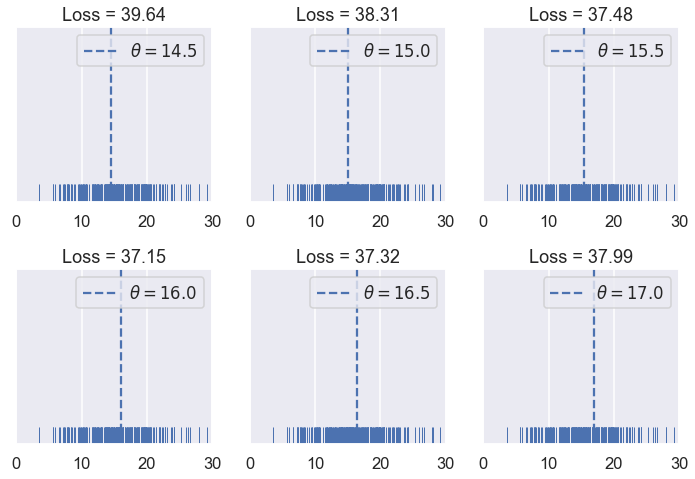
بنفس الطريقة السابقة، يمكن القيام برسم بياني تفاعلي لملاحظة التغير مع تغيير قيمة $ \theta $:
mse_interact(theta=(13, 17, 0.25),
y_vals=tips['pcttip'],
xlims=(0, 30))
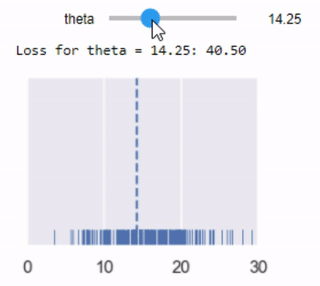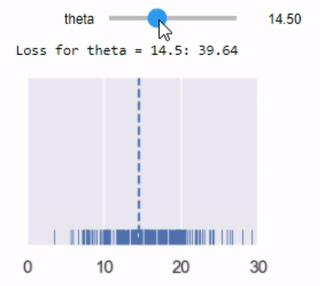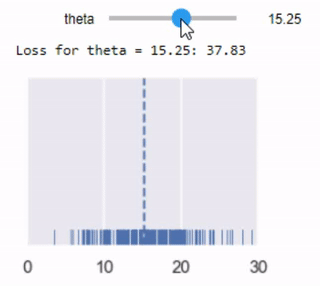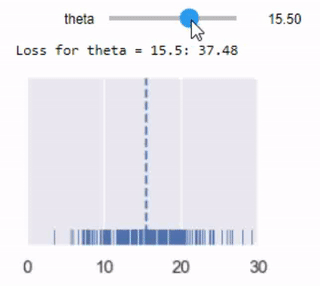
نلاحظ ان افضل قيمة ل $ \theta $ هي 16.00، اعلى بقليل من توقعنا الأول 15% لكل إكرامية.
تبسيط الدالة
قمنا بتعريف أول دالة خسارة لنا، الخطأ التربيعي المتوسط (MSE). ينتج لنا رقم عالي لقيم $ \theta $ البعيدة عن مجموع البيانات. رياضياً، يمكننا تعريف الدالة كالتالي:
\[\begin{aligned} L(\theta, y_1, y_2, \ldots, y_n) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{aligned}\]ستقوم الدالة بإنتاج أرقام مختلفة للخسارة عندما نقوم بأي تغير سواء ل $ \theta $ أو $ y_1, y_2, \ldots, y_n $. لاحظنا ذلك عند تجربتنا قيم مختلفة ل $ \theta $ وعند إضافتنا قيم اضافيه للبيانات.
كاختصار، يمكننا تعريف المصفوفة: $ \textbf{y} = [ y_1, y_2, \ldots, y_n ] $. ثم نكتب دالة الخطأ التربيعي المتوسط كالتالي:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{aligned}\]تقليل الخسارة
حتى الآن، وجدنا أفضل قيمه ل $ \theta $ بتجربة أكثر من قيمه واختيار أقل قيمه بعد تطبيق دالة الخسارة. على الرغم من فاعلية هذه الطريقة، يمكننا إيجاد طرق أفضل باستخدام خصائص دالة الخسارة.
للمثال التالي، استخدمنا بيانات تحتوي على القيم التالية: $ \textbf{y} = [ 11, 12, 15, 16, 17 ] $.
try_thetas(thetas=[12, 13, 14, 15, 16, 17],
y_vals=[11, 12, 15, 17, 18],
xlims=(10.5, 18.5))

في المثال استخدمنا قيمة ل $ \theta $ بين 12 و 17، عند تغير قيمة $ \theta $، تبدأ نتيجة الدالة مرتفعه (10.92) وتقل حتى نصل إلى $ \theta = 15 $، ثم تزيد بعدها. يمكننا ملاحظة تغير نتيجة دالة الخسارة كلما غيرنا قيمة $ \theta $، لنقارن التغير في كل مرة نقوم فيها بتغير قيمة $ \theta $:
thetas = np.array([12, 13, 14, 15, 16, 17])
y_vals = np.array([11, 12, 15, 17, 18])
losses = [mse_loss(theta, y_vals) for theta in thetas]
plt.scatter(thetas, losses)
plt.title(r'Loss vs. $ \theta $ when $\bf{y}$$ = [11, 12, 15, 17, 18] $')
plt.xlabel(r'$ \theta $ Values')
plt.ylabel('Loss');
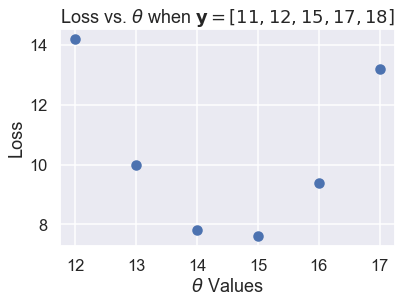
مخطط اَلتَّشَتُّت السابق يظهر توجه للأسفل، ثم للأعلى كما لاحظنا مسبقاً. يمكننا استخدام المزيد من قيم $ \theta $ لمشاهدة كامل المنحنى عندما تتغير الخسارة كلما غيرنا قيمة $ \theta $.
thetas = np.arange(12, 17.1, 0.05)
y_vals = np.array([11, 12, 15, 17, 18])
losses = [mse_loss(theta, y_vals) for theta in thetas]
plt.plot(thetas, losses)
plt.title(r'Loss vs. $ \theta $ when $\bf{y}$$ = [11, 12, 15, 17, 18] $')
plt.xlabel(r'$ \theta $ Values')
plt.ylabel('Loss');
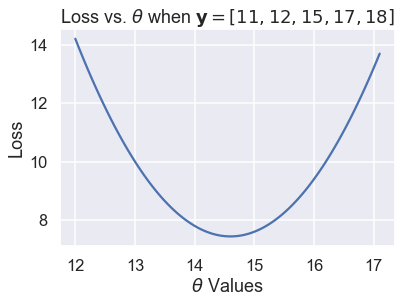
الرسم البياني السابق يؤكد لنا أن $ \theta = 15 $ لم تكن الخيار الأفضل؛ رقم ل $ \theta $ بين 14 و 15 كان قيمة الخسارة فيه أقل. يمكننا استخدام التفاضل والتكامل وحساب قيمة ذلك الرقم بالضبط. بقيمة خسارة أقل، مشتقة دالة الخسارة للقيمة $ \theta $ تكون 0.
نبدأ أولاً بدالة الخسارة التي عرفناها:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{aligned}\]ثم نقوم بإدخال نقاطنا $ \textbf{y} = [11, 12, 15, 17, 18] $ للمعادلة:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{5} \big((11 - \theta)^2 + (12 - \theta)^2 + (15 - \theta)^2 + (17 - \theta)^2 + (18 - \theta)^2 \big)\\ \end{aligned}\]لحساب قيمة $ \theta $ التي تقلل من دالة الخسارة، نقوم بحساب المشتقة ل $ \theta $:
\[\begin{aligned} \frac{\partial}{\partial \theta} L(\theta, \textbf{y}) &= \frac{1}{5} \big(-2(11 - \theta) - 2(12 - \theta) - 2(15 - \theta) - 2(17 - \theta) -2(18 - \theta) \big)\\ &= \frac{1}{5} \big(10 \cdot \theta - 146 \big)\\ \end{aligned}\]ثم نقوم بالبحث عن قيمة $ \theta $ التي مشتقتُها تساوي صفر:
\[\begin{aligned} \frac{1}{5} \big(10 \cdot \theta - 146 \big) &= 0 \\ 10 \cdot \theta - 146 &= 0 \\ \theta &= 14.6 \end{aligned}\]وجدنا قيمة $ \theta $ الأقل، وكما هو متوقع، كانت بين 14 و 15. نرمز لقيمة $ \theta $ ذات الأقل خسارة بالرمز $ \hat{\theta} $. الآن، للبيانات التالية $ \textbf{y} = [11, 12, 15, 17, 18] $ و دالة الخسارة MSE:
\[\hat{\theta} = 14.6\]إذا حسبنا متوسط البيانات لدينا، نلاحظ التالي:
\[\text{mean} (\textbf{y}) = \hat{\theta} = 14.6\]تقليل الخطأ التربيعي المتوسط
كما هو واضح، النتيجة السابقة (تساوي قيمة المتوسط مع $ \hat{\theta} $ ) ليست مجرد صدفه؛ المتوسط لقيم البيانات دائماً ما يساوي $ \hat{\theta} $، وقيمة $ \theta $ التي تقلل من الخسارة بدالة MSE.
لعرض ذلك، نأخذ مشتقة دالة الخسارة مره أخرى. ولكن بدلاً من إضافة البيانات إليها، نبقي الرمز $ y_i $ لنعممها على جميع البيانات.
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \frac{\partial}{\partial \theta} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \\ &= -\frac{2}{n} \sum_{i = 1}^{n} (y_i - \theta) \\ \end{aligned}\]بما أننا لم نعوض أي قيمة للمتغير $ y_i $، يمكن أن نستخدم المعادلة على أي بيانات بأي حجم.
الآن، نعوض قيمة المشتقة بصفر ونحاول إيجاد $ \theta $ لإيجاد أقل قيمة لدالة الخسارة كما فعلنا سابقاً:
\[\begin{aligned} -\frac{2}{n} \sum_{i = 1}^{n} (y_i - \theta) &= 0 \\ \sum_{i = 1}^{n} (y_i - \theta) &= 0 \\ \sum_{i = 1}^{n} y_i - \sum_{i = 1}^{n} \theta &= 0 \\ \sum_{i = 1}^{n} \theta &= \sum_{i = 1}^{n} y_i \\ n \cdot \theta &= y_1 + \ldots + y_n \\ \theta &= \frac{y_1 + \ldots + y_n}{n} \\ \hat \theta = \theta &= \text{mean} (\textbf{y}) \end{aligned}\]نلاحظ كما هو واضح، أن هناك قيمه واحدة ل $ \theta $ التي تعطي أقل قيمه ل MSE أياً كانت القيم داخل البيانات. للخطأ التربيعي المتوسط، نعلم أن $ \hat{\theta} $ هي دائماً تساوي المتوسط للبيانات.
العودة للبيانات الأصلية
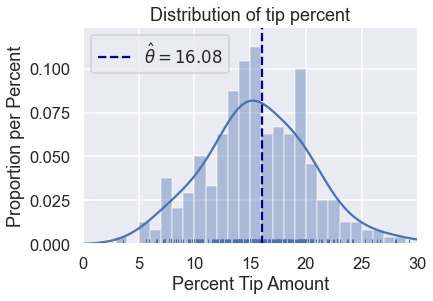
ليس علينا اختبار أي قيم أعلى ل $ \theta $ كما فعلنا مسبقاً. يمكننا إيجاد متوسط الإكراميات ويكفي:
np.mean(tips['pcttip'])
16.08025817225047
لنرسمه:
sns.distplot(tips['pcttip'], bins=np.arange(30), rug=True)
plt.axvline(x=16.08, c='darkblue', linestyle='--', label=r'$ \hat \theta = 16.08$')
plt.legend()
plt.xlim(0, 30)
plt.title('Distribution of tip percent')
plt.xlabel('Percent Tip Amount')
plt.ylabel('Proportion per Percent');
ملخص دالة الخسارة
قمنا بالتعرف على نموذج ثابت، نموذج دائِمًا ما ينتج لنا نفس الرقم لكل بياناتنا.
و تعرفنا على دالة الخسارة $ L(\theta, \textbf{y}) $ التي تقيس مدى كفاءة قيمه معينة ل $ \theta $ للبيانات. في هذا الجزء تعرفنا أيضا على دالة خسارة الخطأ التربيعي المتوسط وأظهرنا أن $ \hat{\theta} = \text{mean}(\textbf{y}) $ للنموذج الثابت.
الطريقة التي استخدمناها في هذا الجزء والتي تطبق على اي نوع من النماذج:
- اختيار النموذج.
- اختيار دالة الخسارة.
- تدريب النموذج عن طريق تقليل قيمة الخسارة.
في هذا الكتاب، جميع طرق إنشاء النماذج تبدأ وتتوسع من أي من هذه النقاط.
دالتي الخسارة Absolute و Huber
لتدريب نموذج، نختار دالة خسارة ومتغيرات النموذج التي تقلل من الخسارة. في الجزء السابق، تعرفنا على دالة الخسارة MSE:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{aligned}\]استخدمنا نموذج ثابت يتوقع نفس الرقم $ \theta $ لجميع البيانات. عندما دربنا النموذج باستخدام دالة الخسارة MSE، وجدنا أن $ \hat{\theta} = \text{mean} (\textbf{y}) $. في بيانات الإكراميات، وجدنا أن النموذج يتوقع 16.8% كونها هي متوسط نسب الإكراميات.
في هذا الجزء، سنتعرف على دالتين خسارة هما متوسط الخطأ الحتمي Mean Absolute Error (MAE) و هوبر Huber.
متوسط الخطأ الحتمي
الآن، سنبقي النموذج كما هو لكن سنغير دالة الخسارة. بدلاً من أخذ الفرق التربيعي بين كل نقطة وتوقعنا، هذه الدالة تأخذ الفرق الحتمي:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n} |y_i - \theta| \\ \end{aligned}\]مقارنة بين MSE و MAE
يعرف الكاتب أولاً دوال سيستخدمها للمقارنة بين MSE و MAE. معرفة معنى الكود البرمجي هنا لا يهم.
tips = sns.load_dataset('tips')
tips['pcttip'] = tips['tip'] / tips['total_bill'] * 100
def mse_loss(theta, y_vals):
return np.mean((y_vals - theta) ** 2)
def abs_loss(theta, y_vals):
return np.mean(np.abs(y_vals - theta))
def compare_mse_abs(thetas, y_vals, xlims, figsize=(10, 7), cols=3):
if not isinstance(y_vals, np.ndarray):
y_vals = np.array(y_vals)
rows = int(np.ceil(len(thetas) / cols))
plt.figure(figsize=figsize)
for i, theta in enumerate(thetas):
ax = plt.subplot(rows, cols, i + 1)
sns.rugplot(y_vals, height=0.1, ax=ax)
plt.axvline(theta, linestyle='--',
label=rf'$ \theta = {theta} $')
plt.title(f'MSE = {mse_loss(theta, y_vals):.2f}\n'
f'MAE = {abs_loss(theta, y_vals):.2f}')
plt.xlim(*xlims)
plt.yticks([])
plt.legend()
plt.tight_layout()
compare_mse_abs(thetas=[11, 12, 13, 14, 15, 16],
y_vals=[14], xlims=(10, 17))
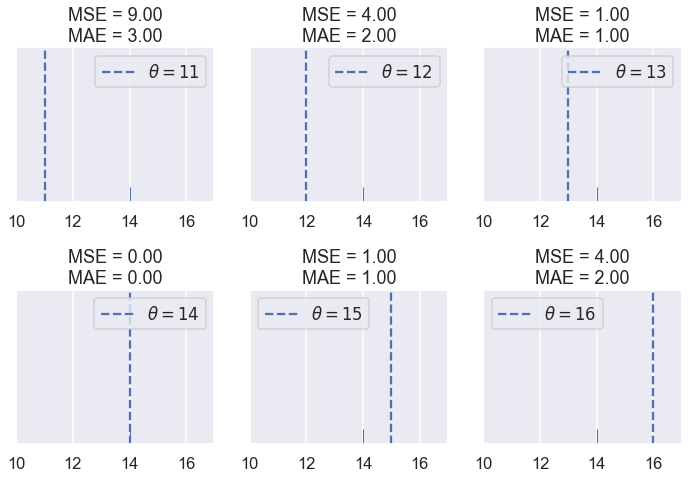
نلاحظ أن MSE عادة ما تكون أعلى من MAE كون دالة الخسارة فيها تربيعية. لنرى ما يحدث عندما يكون لدينا الخمس نقاط التالية: $ \textbf{y} = [ 12.1, 12.8, 14.9, 16.3, 17.2 ] $
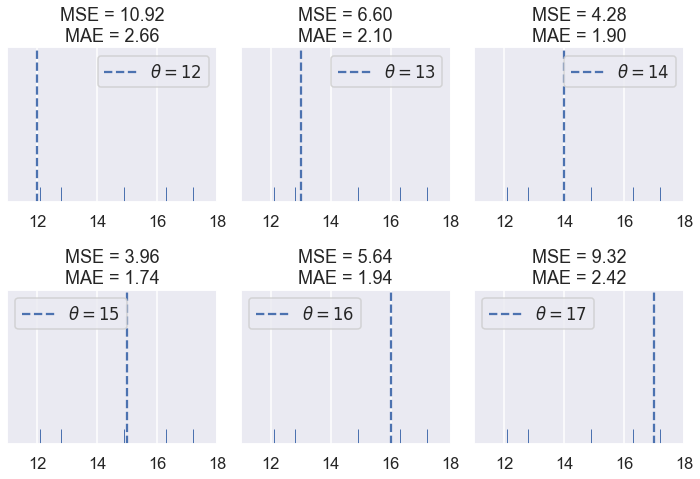
تذكر أن نتيجة دالة الخسارة لا تهمنا كثيراً؛ فهي تهمنا فقط بمقارنة القيمة المختلفة ل $ \theta $. عندما نختار دالة خسارة، سنبحث عن $ \hat{\theta} $، قيمة $ \theta $ التي لديها أقل قيمه للخسارة. لذا، نحن نهتم ما ذا كانت دالة الخسارة تنتج نتائج مختلفة ل $ \hat{\theta} $.
حتى الآن، كلا دالتي الخسارة متفقتان على $ \hat{\theta} $. لو لاحظنا، سنرى بعض الاختلافات. لنرسم نتائج الخسارة مع $ \theta $ لكل قيمه لدينا:
thetas = np.array([12, 13, 14, 15, 16, 17])
y_vals = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
mse_losses = [mse_loss(theta, y_vals) for theta in thetas]
abs_losses = [abs_loss(theta, y_vals) for theta in thetas]
plt.scatter(thetas, mse_losses, label='MSE')
plt.scatter(thetas, abs_losses, label='MAE')
plt.title(r'Loss vs. $ \theta $ when $ \bf{y}$$= [ 12.1, 12.8, 14.9, 16.3, 17.2 ] $')
plt.xlabel(r'$ \theta $ Values')
plt.ylabel('Loss')
plt.legend();
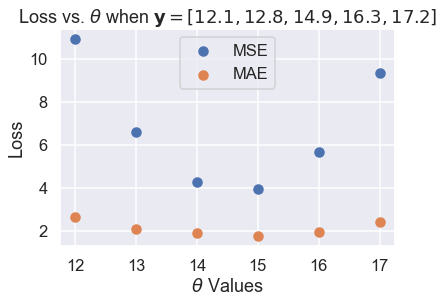
ثم، نستخدم قيم أكثر ل $ \theta $ ليكون المنحنى أكثر سلاسة:
thetas = np.arange(12, 17.1, 0.05)
y_vals = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
mse_losses = [mse_loss(theta, y_vals) for theta in thetas]
abs_losses = [abs_loss(theta, y_vals) for theta in thetas]
plt.plot(thetas, mse_losses, label='MSE')
plt.plot(thetas, abs_losses, label='MAE')
plt.title(r'Loss vs. $ \theta $ when $ \bf{y}$$ = [ 12.1, 12.8, 14.9, 16.3, 17.2 ] $')
plt.xlabel(r'$ \theta $ Values')
plt.ylabel('Loss')
plt.legend();
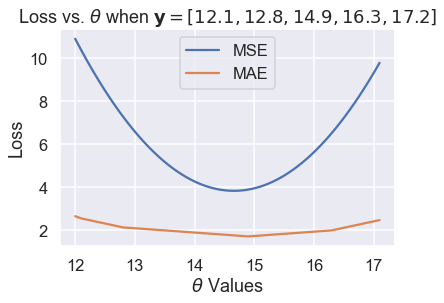
ثم، نقرب الرسم البياني إلى القيم بين 1.5 و 5 على المحور y لنرى الفرق على القيم الدنيا بشكل أوضح. حدثنا القيم الدنيا بخطوط مُنَقَّطَة:
thetas = np.arange(12, 17.1, 0.05)
y_vals = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
mse_losses = [mse_loss(theta, y_vals) for theta in thetas]
abs_losses = [abs_loss(theta, y_vals) for theta in thetas]
plt.figure(figsize=(7, 5))
plt.plot(thetas, mse_losses, label='MSE')
plt.plot(thetas, abs_losses, label='MAE')
plt.axvline(np.mean(y_vals), c=sns.color_palette()[0], linestyle='--',
alpha=0.7, label='Minimum MSE')
plt.axvline(np.median(y_vals), c=sns.color_palette()[1], linestyle='--',
alpha=0.7, label='Minimum MAE')
plt.title(r'Loss vs. $ \theta $ when $ \bf{y}$$ = [ 12.1, 12.8, 14.9, 16.3, 17.2 ] $')
plt.xlabel(r'$ \theta $ Values')
plt.ylabel('Loss')
plt.ylim(1.5, 5)
plt.legend()
plt.tight_layout();
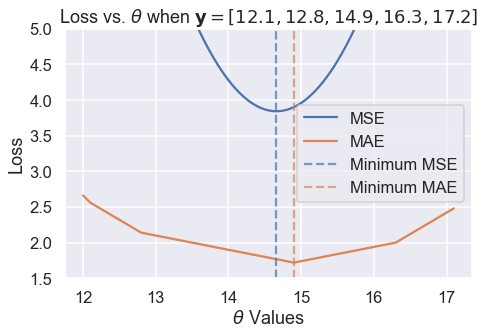
وجدنا بعد تجربتنا أن MSE و MAE قد ينتج عنهما قيم مختلفة ل $ \hat{\theta} $ لنفس البيانات. تحليل أكثر دقه أوضح لنا متى يكون الاختلاف، وسببه.
القيم الشاذة
أحد الاختلافات التي نلاحظها في الرسم البياني السابق لقيمة الخسارة و $ \theta $ هو شكل منحنى الخسارة. رسم MSE أنتج لنا منحنى قطعي مُكافئ. 📝
بينما رسم MAE أنتج لنا لما يبدو وكأنها خطوط متصلة ببعضها. هذا يبدو مفهوماً إذا ما أخذنا بالاعتبار أن دالة القيمة الحتمية هي خطيه، لذا أخذ المتوسط للكثير من الدوال الحتمية سيظهر لنا نواتج شبه خطيه.
بما أن MSE تعتمد على الخطأ التربيعي، ستتأثر أكثر بالقيم الشاذة. إذا كانت $ \theta = 10 $ واحد النقاط كانت 110، قيمة الخطأ في MSE لهذه القيمة ستكون $ (10 - 110)^2 = 10000 $ بينما في MAE، ستكون $ |10 - 110| = 100 $. يمكننا رسم ذلك عن طريق أخذ مصفوفة من ثلاث نقاط $ \textbf{y} = [ 12, 13, 14 ] $ والمقارنة بين منحنيا الخسارة و $ \theta $ ل MSE و MAE.
# دالة تم كتابتها لتساعد على ايجاد النتائج ورسم المقارنة
# لا تحتاج للشرح
def compare_mse_abs_curves(y3=14):
thetas = np.arange(11.5, 26.5, 0.1)
y_vals = np.array([12, 13, y3])
mse_losses = [mse_loss(theta, y_vals) for theta in thetas]
abs_losses = [abs_loss(theta, y_vals) for theta in thetas]
mse_abs_diff = min(mse_losses) - min(abs_losses)
mse_losses = [loss - mse_abs_diff for loss in mse_losses]
plt.figure(figsize=(9, 2))
ax = plt.subplot(121)
sns.rugplot(y_vals, height=0.3, ax=ax)
plt.xlim(11.5, 26.5)
plt.xlabel('Points')
ax = plt.subplot(122)
plt.plot(thetas, mse_losses, label='MSE')
plt.plot(thetas, abs_losses, label='MAE')
plt.xlim(11.5, 26.5)
plt.ylim(min(abs_losses) - 1, min(abs_losses) + 10)
plt.xlabel(r'$ \theta $')
plt.ylabel('Loss')
plt.legend()
interact(compare_mse_abs_curves, y3=(14, 25));
كما شرحت سابقاً على الدوال التفاعلية التي قام بتعريفها الكاتب، هذه مثال آخر لها حيث يتحكم الرسم التفاعلي بقيمة المتغير الأخير $ y_3 $ نلاحظ تغير الرسم كلما كبرت قيمة المتغير من 14 إلى 25.
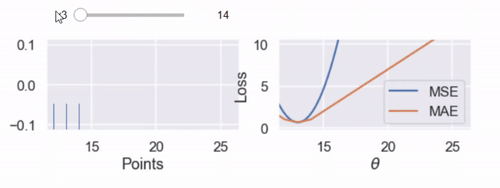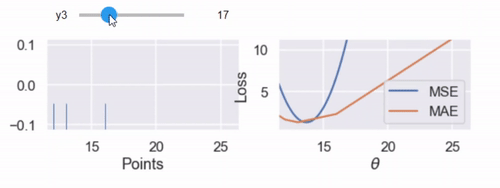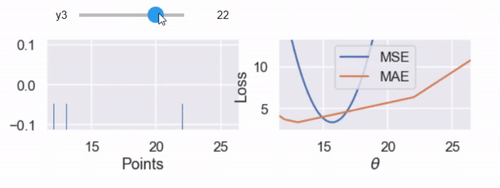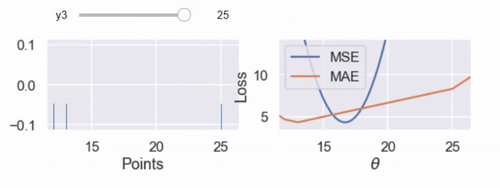
نلاحظ التغيير في المنحنى عندما تكون $ y_3 = 14 $ و $ y_3 = 25 $
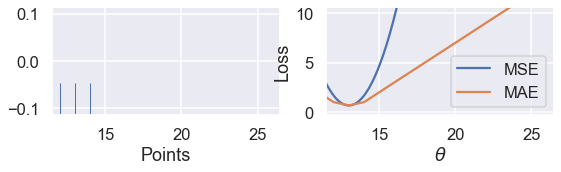
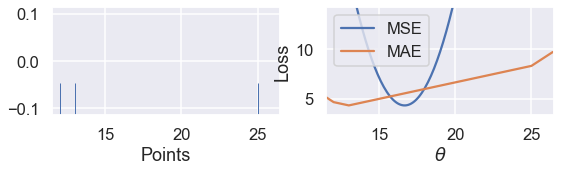
كلما أبعدنا النقطة $ y_3 $ عن بقية البيانات، يتحرك منحنى MSE معه. عندما تكون $ y_3 = 14 $ فإن $ \hat{\theta} = 13 $ في MSE و MAE. ولكن عندما تكون $ y_3 = 25 $ فإن خسارة MSE تكون $ \hat{\theta} = 16.7 $ و MAE $ \hat{\theta} = 13 $، دون تغيير كما كانت مُسبقاً.
تقليل متوسط الخطأ الحتمي
الآن بعد أن تعرفنا على القليل من الفروقات بين MSE و MAE، يمكننا تقليل خسارة MAE لنجعل الفرق بينهما أكثر وضوحاً. كما فعلنا مسبقاً، سنأخذ مشتقة دالة الخسارة ل $ \theta $ ونجعلها تساوي صفر.
ولكن، المرة، يجب أن نتعامل مع احتمالية أن الدالة الحتمية ليست دائماً قابله للاشتقاق. عندما تكون $ x > 0 $ فإن $ \frac{\partial}{\partial x} |x| = 1 $. عندما تكون $ x < 0 $ فإن $ \frac{\partial}{\partial x} |x| = -1 $. على الرغم ان $ |x| $ ليست قابله للاشتقاق عندما تكون $ x = 0 $، سنجعل $ \frac{\partial}{\partial x} |x| = 0 $ لتكون المعادلة سهله للتعامل.
لنتذكر أن معادلة MAE هي:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}|y_i - \theta|\\ &= \frac{1}{n} \left( \sum_{y_i < \theta}|y_i - \theta| + \sum_{y_i = \theta}|y_i - \theta| + \sum_{y_i > \theta}|y_i - \theta| \right)\\ \end{aligned}\]في الجزء الأخير فصلنا الجمع إلى ثلاثة أشكال: واحد عندما تكون $ y_i < \theta $ و أخرى عند $ y_i = \theta $ وأخيره عندما يكون لدينا $ y_i > \theta $. لماذا نجعل عملية الجمع معقدة بهذا الشكل؟ إذا علمنا أن $ y_i < \theta $ فإننا نعلم أن $ |y_i - \theta| < 0 $ ولذلك فإن $ \frac{\partial}{\partial \theta} |y_i - \theta| = -1 $ كما في السابق. وينطبق نفس المنطق على جميع المصطلحات السابق ذكرها ليكون أخذ المشتقات أكثر سهوله.
الآن، نأخذ المشتقة بالنسبة ل $ \theta $ ونجعلها تساوي صفر:
\[\begin{aligned} \frac{1}{n} \left( \sum_{y_i < \theta}(-1) + \sum_{y_i = \theta}(0) + \sum_{y_i > \theta}(1) \right) &= 0 \\ \sum_{y_i < \theta}(-1) + \sum_{y_i > \theta}(1) &= 0 \\ -\sum_{y_i < \theta}(1) + \sum_{y_i > \theta}(1) &= 0 \\ \sum_{y_i < \theta}(1) &= \sum_{y_i > \theta}(1) \\ \end{aligned}\]ماذا تعني النتيجة في الأعلى؟ على اليسار، لدينا قيمه واحدة لكل نقطة أقل من $ \theta $. وعلى اليمين، لدينا قيمه واحدة أيضاً لكل نقطة أعلى من $ \theta $. الآن، لتكون المعادلة صحيحه، نحتاج أن نختار قيمه ل $ \theta $ لديها نفس الرقم لنقطة أقل وأعلى. هذا هو تعريف الوسيط Median لمجموعه من الأرقام. لذا، القيمة الأقل ل $ \theta $ في MAE هي $ \hat \theta = \text{median} (\textbf{y}) $.
عندما يكون لدينا عدد فردي من النقاط، الوسيط هو ببساطه النقطة في الوسط بعد ترتيب النقاط. يمكن أن نرى مثال على ذاك في خمس نقاط، يتم تقليل الخسارة عندما تكون $ \theta $ في الوسيط:
# مره اخرى، الكاتب عرف دالة تساعده على الحساب والرسم
# لا تحتاج لمعرفه معنى الكود البرمجي
def points_and_loss(y_vals, xlim, loss_fn=abs_loss):
thetas = np.arange(xlim[0], xlim[1] + 0.01, 0.05)
abs_losses = [loss_fn(theta, y_vals) for theta in thetas]
plt.figure(figsize=(9, 2))
ax = plt.subplot(121)
sns.rugplot(y_vals, height=0.3, ax=ax)
plt.xlim(*xlim)
plt.xlabel('Points')
ax = plt.subplot(122)
plt.plot(thetas, abs_losses)
plt.xlim(*xlim)
plt.xlabel(r'$ \theta $')
plt.ylabel('Loss')
points_and_loss(np.array([10, 11, 12, 14, 15]), (9, 16))
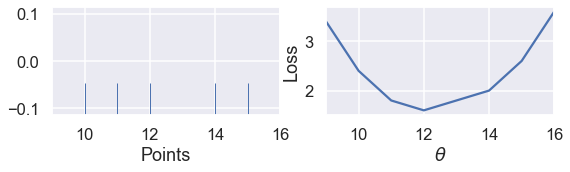
ولكن، عندما يكون لدينا عدد زوجي من الأرقام، تُقَلِّل الخسارة عندما تكون $ \theta $ هي القيمة التي بين النقطتين في الوسط. مثال:
points_and_loss(np.array([10, 11, 14, 15]), (9, 16))
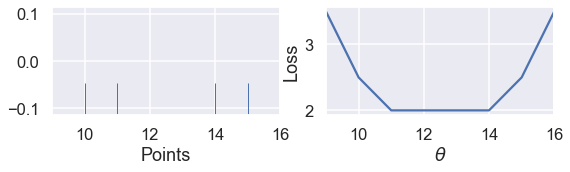
ولا يطبق ذلك عندما نستخدم MSE:
points_and_loss(np.array([10, 11, 14, 15]), (9, 16), mse_loss)
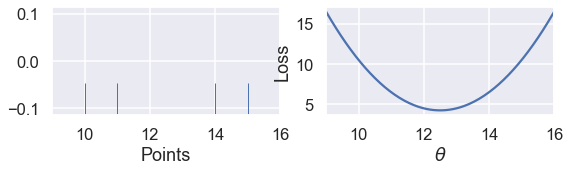
مقارنة MSE و MAE
تحليلنا والمشتقات في الأعلى تُظهر لنا MSE أسهل للاستخدام وإيجاد الاشتقاق ولكنا تتأثر شكل كبير من البيانات الشاذة على عكس MAE. بالنسبة ل MSE، فإن $ \hat{\theta} = \text{mean}(\textbf{y}) $، ول MAE فإن $ \hat{\theta} = \text{median}(\textbf{y}) $. لاحظ أن الوسيط أقل تأثراً بالقيم الشاذة عن المتوسط. ظهر لنا ذلك أثناء تعريف وبناء دالتي الخسارة MSE و MAE.
رأينا أيضاً أن MSE لديها $ \hat{\theta} $ مختلفة، فيها المتوسط الحتمي يمكن أن يكون أكثر احتمال من $ \hat{\theta} $ عندما يكون عدد النقاط في البيانات زوجي.
دالة الخسارة Huber
دالة الخسارة الثالثة يطلق عليها دالة Huber والتي تجمع بين MSE و MAE لتكون لنا دالة خسارة قابله للاشتقاق ولا تتأثر بالقيم الشاذة. تفعل ذلك دالة Huber عن طريق العمل وكأنها دالة MSE لقيم $ \theta $ عندما تكون قريبه من القيم الدنيا والتغيير إلى MAE عندما تكون قيم $ \theta $ بعيدة عن القيم الدنيا.
كما في الغالب، ننشأ دالة خسارة عن طريق أخذ المتوسط لكل خسارة Huber لكل نقطة في بياناتنا.
لنرى نتيجة دالة الخسارة Hurber عندما تكون بياناتنا عبارة عن $ \textbf{y} = [14] $ مع قيم مختلفة ل $ \theta $:
def huber_loss(est, y_obs, alpha = 1):
d = np.abs(est - y_obs)
return np.where(d < alpha,
(est - y_obs)**2 / 2.0,
alpha * (d - alpha / 2.0))
thetas = np.linspace(0, 50, 200)
loss = huber_loss(thetas, np.array([14]), alpha=5)
plt.plot(thetas, loss, label="Huber Loss")
plt.vlines(np.array([14]), -20, -5,colors="r", label="Observation")
plt.xlabel(r"Choice for $\theta$")
plt.ylabel(r"Loss")
plt.legend()
# حفظ النتيجة في ملف PDF
plt.savefig('huber_loss.pdf')
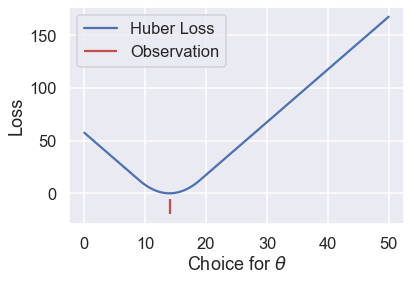
نلاحظ أن خط دالة الخسارة Huber سلس، على عكس MAE. أيضا تزداد خسارة Huber بمعدل خطي، على عكس المعدل التربيعي لمتوسط الخسارة التربيعية.
ولكن لدى دالة خسارة Huber عيب. لاحظ أنها تغيرت من MSE إلى MAE عندما كانت $ \theta $ أبعد عن النقاط. يمكننا التحكم بمدى البعد للحصول على منحنيات خسارة أخرى. مثلاً، يمكننا أن نجعلها تبدأ بالتغيير عندما تكون $ \theta $ أقرب بنقطة عن القيمة الدنيا:
loss = huber_loss(thetas, np.array([14]), alpha=1)
plt.plot(thetas, loss, label="Huber Loss")
plt.vlines(np.array([14]), -20, -5,colors="r", label="Observation")
plt.xlabel(r"Choice for $\theta$")
plt.ylabel(r"Loss")
plt.legend()
# حفظ النتيجة في ملف PDF
plt.savefig('huber_loss.pdf')
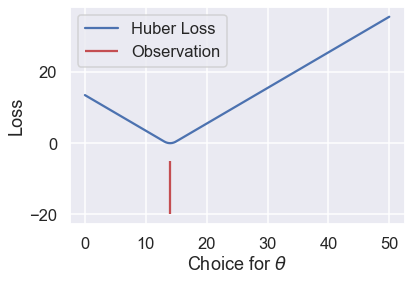
أو يمكننا تغير ذلك وجعلها تتغير عندما تكون $ \theta $ على بعد عشر نقاط من القيمة الدنيا:
loss = huber_loss(thetas, np.array([14]), alpha=10)
plt.plot(thetas, loss, label="Huber Loss")
plt.vlines(np.array([14]), -20, -5,colors="r", label="Observation")
plt.xlabel(r"Choice for $\theta$")
plt.ylabel(r"Loss")
plt.legend()
# حفظ النتيجة في ملف PDF
plt.savefig('huber_loss.pdf')
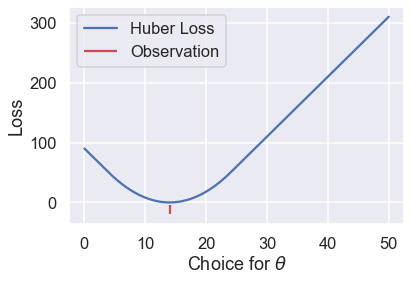
الخيار هنا يكون لنا منحنى مختلف لخط الخسارة مما ينتج لنا أيضا قيم مختلفة ل $ \hat \theta $. إذا أردنا استخدام دالة الخسارة Huber، لدينا مهمة أخرى وهي تحديد نقطة التغيير وجعلها قيمه مناسبة.
يمكننا تعريف دالة Huber رياضياً كالتالي:
\[L_\alpha(\theta, \textbf{y}) = \frac{1}{n} \sum_{i=1}^n \begin{cases} \frac{1}{2}(y_i - \theta)^2 & | y_i - \theta | \le \alpha \\ \alpha ( |y_i - \theta| - \frac{1}{2}\alpha ) & \text{otherwise} \end{cases}\]هي أكثر تعقيداً من دوال الخسارة السابقة لأنها تجمع بين MSE و MAE. المتغير الإضافي $ \alpha $ يحدد مكان نقطة التغيير في دالة Huber من MSE إلى MAE.
محاولة إيجاد مُشتقة دالة Huber عملية مملة ولا تنتج نتائج واضحة ومفهومه كما في MSE و MAE. بدلاً من ذلك، يمكننا استخدام العملية الحسابية المسماة النزول الاشتقاقي لإيجاد القيمة الأقل ل $ \theta $.
ملخص دالتي الخسارة Absolute و Huber
في هذا الجزء، تعرفنا على دالتي خسارة: متوسط الخطأ الحتمي و دالة Huber. ووجدنا أن لنموذج ثابت باستخدام MAE فإن $ \hat{\theta} = \text{median}(\textbf{y}) $.