مبادئ وتقنيات علم البيانات
الفصل الحادي عشر: النزول الاشتقاقي وتحسين النتائج الكمية
فهرس الفصل:
مقدمة
لاستخدام قاعدة بيانات للتنبؤ والتوقع، يجب علينا تكوين نموذجنا بشكل دقيق واختيار دالة خسارة. مثلاً، بيانات الإكراميات، نموذجنا توقع أن نسبة الإكرامية ثابتة لا تتغير. ثم قررنا استخدام دالة الخطأ التربيعي المتوسط MSE ووجدنا النموذج الأقل خسارة.
وجدنا أيضاً أن هناك وصفاً أبسط لدالتي الخسارة الخطأ التربيعي المتوسط و متوسط الخطأ الحتمي وهي: المتوسط والوسيط. ولكن، كلما كان نموذجنا ودالة الخسارة أكثر تعقيداً لن نستطيع إيجاد وصفاً رياضياً مناسب. مثلاً، دالة Huber لديها خصائص مفيده ولكن صعب تمييزها.
يمكننا استخدام الكمبيوتر لحل هذه المشكل بواسطة النزول الاشتقاقي، طريقه حسابية لتقليل دوال الخسارة.
تقليل الخسارة باستخدام برنامج
لنعود للنموذج من الفصل السابق:
\[\theta = C\]سنستخدم دالة الخسارة MSE:
\[\begin{split} \begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{aligned} \end{split}\]للتبسيط، سنستخدم البيانات التالية: $ \textbf{y} = [ 12, 13, 15, 16, 17 ] $. نعلم من خلال تحليلنا للبيانات في الفصل السابق أن قيمة $ \theta $ لدالة الخسارة MSE هي المتوسط $ \text{mean}(\textbf{y}) = 14.6 $. لنرى اذا كان بإمكاننا الحصول على نتيجة عند كتابتنا لبرنامج يوجدها.
إذا قمنا بكتابة برنامج بشكل متقن، فبإمكاننا استخدام نفس البرنامج على أي دالة خسارة لإيجاد أقل قيمة ل $ \theta $، يشمل ذلك دالة Huber المعقدة رياضياً:
\[\begin{split} L_\alpha(\theta, \textbf{y}) = \frac{1}{n} \sum_{i=1}^n \begin{cases} \frac{1}{2}(y_i - \theta)^2 & | y_i - \theta | \le \alpha \\ \alpha ( |y_i - \theta| - \frac{1}{2}\alpha ) & \text{otherwise} \end{cases} \end{split}\]أولاً، نقوم برسم تخطيطي للبيانات. بالجانب الأيمن من الرسم نقوم برسم دالة الخسارة MSE لقيم مختلفة ل $ \theta $:
pts = np.array([12, 13, 15, 16, 17])
points_and_loss(pts, (11, 18), mse)
في الكود البرمجي السابق استخدم الكاتب دالة عرفها مسبقاً بأسم
points_and_loss، تقبل الدالة ثلاث متغيرات، الأولى هي البيانات. المتغير الثاني هي مقاسات أبعاد x-axis ، والقيمة الأخيرة هي نوع دالة الخسارة، والتي هي عبارة عن دالة أخرى عرفها أيضاً بأسمmse. تعريف كلا الدالتين هو كالتالي:def mse(theta, y_vals): return np.mean((y_vals - theta) ** 2) def points_and_loss(y_vals, xlim, loss_fn): thetas = np.arange(xlim[0], xlim[1] + 0.01, 0.05) losses = [loss_fn(theta, y_vals) for theta in thetas] plt.figure(figsize=(9, 2)) ax = plt.subplot(121) sns.rugplot(y_vals, height=0.3, ax=ax) plt.xlim(*xlim) plt.title('Points') plt.xlabel('Tip Percent') ax = plt.subplot(122) plt.plot(thetas, losses) plt.xlim(*xlim) plt.title(loss_fn.__name__) plt.xlabel(r'$ \theta $') plt.ylabel('Loss') plt.legend()
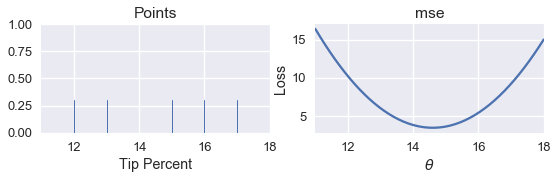
كيف بإمكاننا برمجة برنامج يقوم بإيجاد أقل قيمة ل $ \theta $ أوتوماتيكياً؟ الطريقة الأسهل هي بحساب قيمة الخسارة لأكثر من قيمه ل $ \theta $، ثم نوجد قيمة $ \theta $ ذا الأقل خسارة.
عرفنا دالة بأسم simple_minimize والتي تقبل متغيرات هي دالة الخسارة، مصفوفة البيانات، ومصفوفة بقيم $ \theta $:
def simple_minimize(loss_fn, dataset, thetas):
'''
القيمه النهائيه لهذه الداله هي قيمة θ من بين عدة قيم من θ ذات الأقل خسارة
'''
losses = [loss_fn(theta, dataset) for theta in thetas]
return thetas[np.argmin(losses)]
ثم نعرف دالة لإيجاد قيمة MSE واستخدامها في دالة simple_minimize:
def mse(theta, dataset):
return np.mean((dataset - theta) ** 2)
dataset = np.array([12, 13, 15, 16, 17])
thetas = np.arange(12, 18, 0.1)
simple_minimize(mse, dataset, thetas)
14.599999999999991
النتيجة هذه قريبه للقيمة المتوقعة:
# ايجاد القيمه باستخدام المتوسط
np.mean(dataset)
14.6
الآن يمكننا كتابة دالة لحساب خسارة Huber ورسمها:
def huber_loss(theta, dataset, alpha = 1):
d = np.abs(theta - dataset)
return np.mean(
np.where(d < alpha,
(theta - dataset)**2 / 2.0,
alpha * (d - alpha / 2.0))
)
points_and_loss(pts, (11, 18), huber_loss)
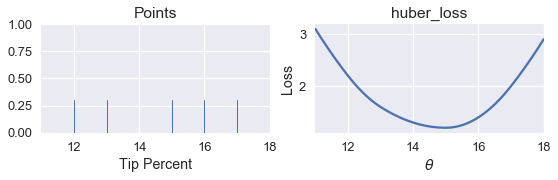
على الرغم أن القيم الدنيا ل $ \theta $ يجب أن تكون أقرب إلى 15، ليس لدينا طريقه لتحليل وإيجاد قيمة $ \theta $ لدالة الخسارة Huber. بدلاً، من ذلك، سنستخدم الدالة simple_minimize:
simple_minimize(huber_loss, dataset, thetas)
14.999999999999989
الآن، لنعود لبيانات نسبة الإكراميات ونوجد أفضل قيمه ل $ \theta $ باستخدام Huber:
tips = sns.load_dataset('tips')
tips['pcttip'] = tips['tip'] / tips['total_bill'] * 100
tips.head()
| pcttip | size | time | day | smoker | sex | tip | total_bill | |
|---|---|---|---|---|---|---|---|---|
| 5.944673 | 2 | Dinner | Sun | No | Female | 1.01 | 16.99 | 0 |
| 16.054159 | 3 | Dinner | Sun | No | Male | 1.66 | 10.34 | 1 |
| 16.658734 | 3 | Dinner | Sun | No | Male | 3.5 | 21.01 | 2 |
| 13.978041 | 2 | Dinner | Sun | No | Male | 3.31 | 23.68 | 3 |
| 14.680765 | 4 | Dinner | Sun | No | Female | 3.61 | 24.59 | 4 |
points_and_loss(tips['pcttip'], (11, 20), huber_loss)
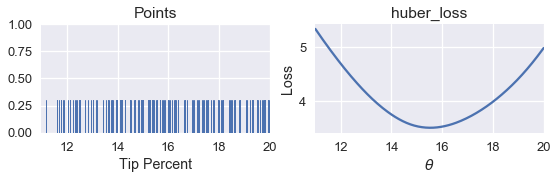
simple_minimize(huber_loss, tips['pcttip'], thetas)
15.499999999999988
نلاحظ أن عند استخدام دالة خسارة Huber كانت النتيجة $ \hat{\theta} = 15.5 $ . يمكننا الآن مقارنة هذه النتيجة مع MSE و MAE:
print(f" MSE: theta_hat = {tips['pcttip'].mean():.2f}")
print(f" MAE: theta_hat = {tips['pcttip'].median():.2f}")
print(f" Huber loss: theta_hat = 15.50")
MSE: theta_hat = 16.08
MAE: theta_hat = 15.48
Huber loss: theta_hat = 15.50
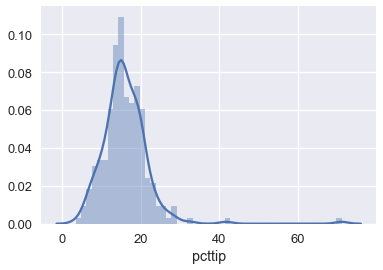
نلاحظ أن دالة Huber أقرب إلى MAE كونها لا تتأثر بشكل كبير بسبب القيم الشاذة على الجانب الأيمن في الرسم البياني التالي لتوزيع بيانات الإكراميات:
sns.distplot(tips['pcttip'], bins=50);
مشاكل simple_minimize
على الرغم من أن دالة simple_minimize تساعدنا على تقليل دالة الخسارة، إلا أن لديها بعض المشاكل التي تجعلها غير مفيده للاستخدام بشكل عام. مشكلتها الأهم هي أنها تعمل فقط مع قيم $ \theta $. مثلاً، في الكود البرمجي التالي، الذي سبق أن استخدمناه في الأعلى، احتجنا لتعريف قيم $ \theta $ يدوياً من 12 إلى 18:
dataset = np.array([12, 13, 15, 16, 17])
thetas = np.arange(12, 18, 0.1)
simple_minimize(mse, dataset, thetas)
كيف وجدنا أنه علينا التحقق من القيم بين 12 و 18؟ احتجنا لمراجعة الرسم البياني لدالة الخسارة ووجدنا أن القيم الدنيا بين تلك القيمتين. هذه الطريقة غير عملية لأننا قمنا بإضافة خطوه معقدة جديده لنماذجنا. بالإضافة لذلك، قمنا بتعريف قيم الزيادة 0.1 بشكل يدوي. ولكن، إذا كانت القيمة المثلى ل $ \theta $ هي 12.043، ستقوم الدالة simple_minimize بتقريب النتيجة إلى 12.00 كونها الأقرب لمضاعفات 0.1
يمكننا حل تلك المشاكل بطريقه واحدة باستخدام ما يسمى بـ النزول الاشتقاقي Gradient Descent.
النزول الاشتقاقي
نحن مُهتمون لبناء دالة تستطيع التقليل من دالة الخسارة دون تقييد المستخدم لتحديد قيم مسبقة ل $ \theta $ للتجربة عليها. بمعنى أصح، بما أن دالة simple_minimize شكلها كالتالي: 📝
simple_minimize(loss_fn, dataset, thetas)
نريد دالة لديها الشكل التالي
minimize(loss_fn, dataset)
لاحظ في الشكل الذي نبحث عنه، لا يحتاج المستخدم لإضافة لقيم مسبقة ل $ \theta $ في المتغيرات المطلوبة لدالة تقليل الخسارة
minimize.
تحتاج هذه الدالة لإيجاد قيم $ \theta $ الأقل خسارة أوتوماتيكياً أياً كان حجمها. سنستخدم طريقة تسمى بالنزول الاشتقاقي لبناء الدالة الجديدة المسماة minimize.
الفكرة
كما في دوال الخسارة، سنتحدث عن فكرة النزول الاشتقاقي أولاً، ثم نتعرف ونفهم العملية الرياضية فيها.
بما أن الدالة minimize لا يقدم لها قيم ل $ \theta $ للتجربة عليها، نقوم باختيار قيمه ل $ \theta $ بأي مكانٍ. ثم، نقوم بشكل تكراري بتحسين نتائج $ \theta $. وللتحسين من النتائج، نقوم بملاحظة الميلان Slope لتلك القيمة من $ \theta $ التي اخترناها في الرسم البياني.
مثلاً، سنستخدم MSE على البيانات التالية $ \textbf{y} = [ 12.1, 12.8, 14.9, 16.3, 17.2 ] $ وقيمة $ \theta $ التي اختراناها هي 12:
pts = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
plot_loss(pts, (11, 18), mse)
plot_theta_on_loss(pts, 12, mse)
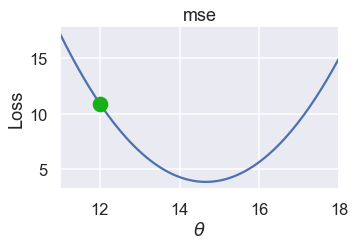
استخدم الكاتب 3 دوال كما فعل مسبقاً لتساعده على القيام بالعملية الحسابية والرسم البياني وهي
plot_loss،plot_theta_on_lossوplot_tangent_on_loss. والكود البرمجي في الأسفل هو تعريف لكل الدوال:def plot_loss(y_vals, xlim, loss_fn): thetas = np.arange(xlim[0], xlim[1] + 0.01, 0.05) losses = [loss_fn(theta, y_vals) for theta in thetas] plt.figure(figsize=(5, 3)) plt.plot(thetas, losses, zorder=1) plt.xlim(*xlim) plt.title(loss_fn.__name__) plt.xlabel(r'$ \theta $') plt.ylabel('Loss') def plot_theta_on_loss(y_vals, theta, loss_fn, **kwargs): loss = loss_fn(theta, y_vals) default_args = dict(label=r'$ \theta $', zorder=2, s=200, c=sns.xkcd_rgb['green']) plt.scatter([theta], [loss], **{**default_args, **kwargs}) def plot_tangent_on_loss(y_vals, theta, loss_fn, eps=1e-6): slope = ((loss_fn(theta + eps, y_vals) - loss_fn(theta - eps, y_vals)) / (2 * eps)) xs = np.arange(theta - 1, theta + 1, 0.05) ys = loss_fn(theta, y_vals) + slope * (xs - theta) plt.plot(xs, ys, zorder=3, c=sns.xkcd_rgb['green'], linestyle='--')
نريد اختيار قيمه جديده ل $ \theta $ لتقليل الخسارة. ولعمل ذلك، كما ذكرنا سابقاً، نلاحظ الميلان لقيمة $ \theta= 12 $:
pts = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
plot_loss(pts, (11, 18), mse)
plot_tangent_on_loss(pts, 12, mse)
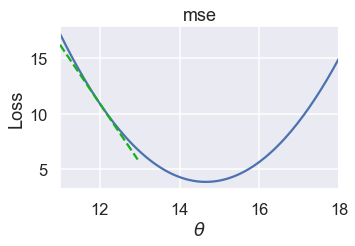
قيمة الميلان سلبية، يعني ذلك أن زيادة قيمة $ \theta $ سيقلل من الخسارة. إذا كانت $ \theta= 16.5 $، فإن قيمة الميلان ستكون موجبه:
pts = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
plot_loss(pts, (11, 18), mse)
plot_tangent_on_loss(pts, 16.5, mse)
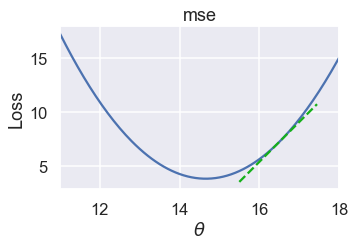
عندما تكون نتيجة الميلان إيجابية، فإن تقليل قيمة $ \theta $ سيقلل الخسارة.
الميلان في الخط يخبرنا بأي اتجاه نختار $ \theta $ لتقليل الخسارة. إذا كان الميلان نتيجته سلبية، فنحتاج لتحرك $ \theta $ إلى الجانب الإيجابي. وإذا كان إيجابياً، فعلينا تحريك $ \theta $ إلى الجانب السلبي. رياضاً، نقول التالي:
\[\theta^{(t+1)} = \theta^{(t)} - \frac{\partial}{\partial \theta} L(\theta^{(t)}, \textbf{y})\]وفيها $ \theta^{(t)} $ هي القيمة الحالية، و $ \theta^{(t+1)} $ هي القيمة التالية.
بالنسبة ل MSE، فستكون كالتالي:
\[\begin{split} \begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2\\ \frac{\partial}{\partial \hat{\theta}} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \\ &= -\frac{2}{n} \sum_{i = 1}^{n} (y_i - \theta) \\ \end{aligned} \end{split}\]عندما تكون $ \theta^{(t)} = 12 $، فالنتيجة هي $ -\frac{2}{n} \sum_{i = 1}^{n} (y_i - \theta) = -5.32 $، ثم نستخدمها بالمعادلة السابقة: $ \theta^{(t+1)} = 12 - (-5.32) = 17.32 $
رسمنا في الأسفل القيمة السابقة ل $ \theta $ بدائرة مفرغة بحدود خضراء والقيمة الجديدة لها بدائرة باللون الأخضر:
pts = np.array([12.1, 12.8, 14.9, 16.3, 17.2])
plot_loss(pts, (11, 18), mse)
plot_theta_on_loss(pts, 12, mse, c='none',
edgecolor=sns.xkcd_rgb['green'], linewidth=2)
plot_theta_on_loss(pts, 17.32, mse)
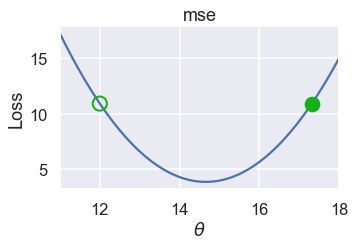
على الرغم أن $ \theta $ انتقلت إلى الجانب الأيمن، لكنها لا زالت بعيده جداً عن القيمة الدنيا. يمكننا حل ذلك عن طريق ضرب الميلان بقيمه صغيرة قبل طرحه من $ \theta $. والعملية الحسابية النهاية ستبدو كالتالي:
\[\theta^{(t+1)} = \theta^{(t)} - \alpha \cdot \frac{\partial}{\partial \theta} L(\theta^{(t)}, \textbf{y})\]وفيها $ \alpha $ هي قيمه ثابتة صغيرة. مثلاً، إذا حددنا قيمة $ \alpha = 0.3 $، فإن القيمة الجديدة ل $ \theta^{(t+1)} $ ستكون:
plot_one_gd_iter(pts, 12, mse, grad_mse)
old theta: 12
new theta: 13.596
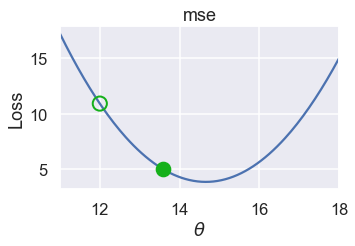
عرف الكاتب دالة جديده بأسم
plot_one_gd_iterتقوم بكتابة ورسم بياني لقيمه $ \theta $ السابقة والجديدة بعد القيام بالعملية الحسابية المشروحة مسبقاً، استخدم الكاتب أيضاً دالة بأسمgrad_mseوهي تعريف لدالةmseباستخدام النزول الاشتقاقي، الكود البرمجي لكلا الدالتين:def plot_one_gd_iter(y_vals, theta, loss_fn, grad_loss, alpha=0.3): new_theta = theta - alpha * grad_loss(theta, y_vals) plot_loss(pts, (11, 18), loss_fn) plot_theta_on_loss(pts, theta, loss_fn, c='none', edgecolor=sns.xkcd_rgb['green'], linewidth=2) plot_theta_on_loss(pts, new_theta, loss_fn) print(f'old theta: {theta}') print(f'new theta: {new_theta}') def grad_mse(theta, y_vals): return -2 * np.mean(y_vals - theta)
في الرسم التالي، قيم $ \theta $ بعد عدة تكرارات بنفس الطريقة السابقة. لاحظ أن $ \theta $ تتغير بشكل بسيط كلما اقتربنا من القيمة الدنيا لأن الميلان أيضاً أصبحت قيمته أقل:
plot_one_gd_iter(pts, 13.60, mse, grad_mse)
old theta: 13.6
new theta: 14.236
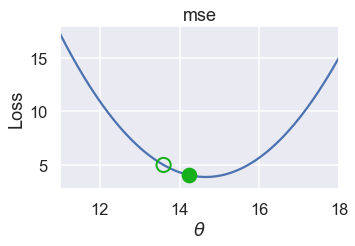
plot_one_gd_iter(pts, 14.24, mse, grad_mse)
old theta: 14.24
new theta: 14.492
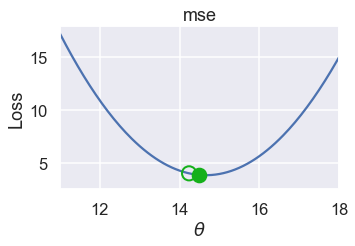
plot_one_gd_iter(pts, 14.49, mse, grad_mse)
old theta: 14.49
new theta: 14.592
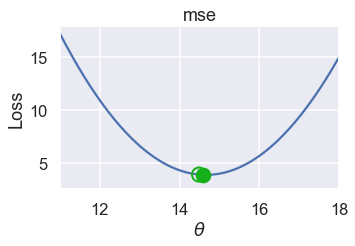
تحليل النزول الاشتقاقي
لدينا الآن فكرة عن طريقة عمل خوارزمية النزول الاشتقاقي:
- اختيار قيمه أوليه ل $ \theta $ ( في العادة تكون 0 ).
- إجراء العملية الحسابية $ \theta - \alpha \cdot \frac{\partial}{\partial \theta} L(\theta, \textbf{y}) $ عليها وحفظ النتيجة كقيمه جديده ل $ \theta $.
- تكرار العملية حتى تتوقف $ \theta $ عن التغير.
غالباً ستلاحظ استخدام رمز النزول (الانحدار) $ \nabla_\theta $ بدلاً من الاشتقاق الجزئي $ \frac{\partial}{\partial \theta} $. كلا الرمزين متشابهان، ولكن بما أنا استخدام رمز النزول أكثر بشكل عام، فسنقوم باستخدامه في المعادلة:
\[\theta^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_\theta L(\theta^{(t)}, \textbf{y})\]لمراجعة الرموز:
- $ \theta^{(t)} $ هي التوقع الحالي ل $ \theta^{*} $ في التكرار $ t $.
- $ \theta^{(t+1)} $ القيمة التالية ل $ \theta $.
- $ \alpha $ يطلق عليها معدل التعلّم Learning Rate، وعادة ما تكون رقم صغير ثابت. في بعض المرات من المفيد أن تبدأ برقم عالي ل $ \alpha $ والتقليل منه. إذا تغيرت قيمة $ \alpha $ بين عمليات التكرار، نستخدم الرمز $ \alpha^t $ لتوضيح تغير $ \alpha $ في $ t $.
- $ \nabla_\theta L(\theta^{(t)}, \textbf{y}) $ هي اشتقاق جزئي لدالة الخسارة فيها قيمه متوقعة ل $ \theta $ في التكرار $ t $.
يمكننا ملاحظة أهمية استخدام دالة خسارة قابله للتفاضل: $ \nabla_\theta L(\theta, \textbf{y}) $ هي جزء مهم من خوارزمية النزول الاشتقاقي. (على الرغم أن بالإمكان توقع قيمة النزول (الإنحدار) بحساب الفرق في الخسارة بين قيمتين $ \theta $ وقسمتها على المسافه بينهما، لكن ذلك يزيد من مدة إيجاد النتيجة للنزول الاشتقاقي بشكل كبير مما يجعلها غير مفيده للاستخدام).
خوارزمية النزول الاشتقاقي بسيطه ومفيده بشكل كبير وذلك لإن بإمكاننا استخدامها في كثير من انواع النماذج والكثير من دوال الخسارة. هي الطريقة الحسابيه الأهم لضبط النماذج، بما فيها الإنحدار الخطي على بيانات بحجم كبير والشبكات العصبيه.
تعريف دالة minimize
الآن نعود لمهمتنا الأساسية: تعريف دالة minimize. سنحتاج للتعديل قليلاً من تعريف الدالة كوننا نريد إيجاد النزول الاشتقاقي لدالة الخسارة:
def minimize(loss_fn, grad_loss_fn, dataset, alpha=0.2, progress=True):
'''
تستخدم النزول الاشتقاقي للتقليل من دالة الخسارة loss_fn.
تنتج لنا الداله القيمه الصغرى ل theta_hat (θ^) عندما يكون
التغيير اقل من 0.001 بين التكرارات.
'''
theta = 0
while True:
if progress:
print(f'theta: {theta:.2f} | loss: {loss_fn(theta, dataset):.2f}')
gradient = grad_loss_fn(theta, dataset)
new_theta = theta - alpha * gradient
if abs(new_theta - theta) < 0.001:
return new_theta
theta = new_theta
ثم يمكننا تعريف دوال تقوم بحساب MSE و نزولها (انحدارها):
def mse(theta, y_vals):
return np.mean((y_vals - theta) ** 2)
def grad_mse(theta, y_vals):
return -2 * np.mean(y_vals - theta)
أخيراً، يمكننا استخدام الدالة minimize لحساب قيمة $ \theta $ الأدنى للبيانات التالية $ \textbf{y} = [12.1, 12.8, 14.9, 16.3, 17.2] $
%%time
theta = minimize(mse, grad_mse, np.array([12.1, 12.8, 14.9, 16.3, 17.2]))
print(f'Minimizing theta: {theta}')
print()
theta: 0.00 | loss: 218.76
theta: 5.86 | loss: 81.21
theta: 9.38 | loss: 31.70
theta: 11.49 | loss: 13.87
theta: 12.76 | loss: 7.45
theta: 13.52 | loss: 5.14
theta: 13.98 | loss: 4.31
theta: 14.25 | loss: 4.01
theta: 14.41 | loss: 3.90
theta: 14.51 | loss: 3.86
theta: 14.57 | loss: 3.85
theta: 14.61 | loss: 3.85
theta: 14.63 | loss: 3.84
theta: 14.64 | loss: 3.84
theta: 14.65 | loss: 3.84
theta: 14.65 | loss: 3.84
theta: 14.66 | loss: 3.84
theta: 14.66 | loss: 3.84
Minimizing theta: 14.658511131035242
CPU times: user 7.88 ms, sys: 3.58 ms, total: 11.5 ms
Wall time: 8.54 ms
نلاحظ أن النزول الاشتقاقي قام بإيجاد نفس النتيجة بشكل سريع ل:
np.mean([12.1, 12.8, 14.9, 16.3, 17.2])
14.66
تقليل خسارة Huber
الآن، يمكننا تطبيق النزول الاشتقاقي للتقليل من دالة الخسارة Huber على بيانات الإكراميات.
tips = sns.load_dataset('tips')
tips['pcttip'] = tips['tip'] / tips['total_bill'] * 100
دالة الخسارة Huber تعرف كالتالي:
\[\begin{split} L_\delta(\theta, \textbf{y}) = \frac{1}{n} \sum_{i=1}^n \begin{cases} \frac{1}{2}(y_i - \theta)^2 & | y_i - \theta | \le \delta \\ \delta (|y_i - \theta| - \frac{1}{2} \delta ) & \text{otherwise} \end{cases} \end{split}\]والنزول الاشتقاقي لدالة Huber:
\[\begin{split} \nabla_{\theta} L_\delta(\theta, \textbf{y}) = \frac{1}{n} \sum_{i=1}^n \begin{cases} -(y_i - \theta) & | y_i - \theta | \le \delta \\ - \delta \cdot \text{sign} (y_i - \theta) & \text{otherwise} \end{cases} \end{split}\](لاحظ أننا في التعاريف السابقة لدالة خسارة Huber استخدمنا المتغير $ \alpha $ للإشارة لنقطة الانتقال. ولإبعاد الشك بينها وبين $ \alpha $ المستخدمة في النزول الاشتقاقي، قمنا بتغير رمز نقطة الانتقال في دالة الخسارة Huber إلى الرمز $ \delta $.)
def huber_loss(theta, dataset, delta = 1):
d = np.abs(theta - dataset)
return np.mean(
np.where(d <= delta,
(theta - dataset)**2 / 2.0,
delta * (d - delta / 2.0))
)
def grad_huber_loss(theta, dataset, delta = 1):
d = np.abs(theta - dataset)
return np.mean(
np.where(d <= delta,
-(dataset - theta),
-delta * np.sign(dataset - theta))
)
لنقوم بالتقليل من دالة الخسارة Huber في بيانات الإكرامية:
%%time
theta = minimize(huber_loss, grad_huber_loss, tips['pcttip'], progress=False)
print(f'Minimizing theta: {theta}')
print()
Minimizing theta: 15.506849531471964
CPU times: user 194 ms, sys: 4.13 ms, total: 198 ms
Wall time: 208 ms
ملخص النزول الاشتقاقي
يوفر لنا النزول الاشتقاقي طريقه عامله للتقليل من دالة الخسارة عندما لا نستطيع إيجاد القيمة الدنيا ل $ \theta $. عندما يكون نموذجنا ودالة الخسارة أكثر تعقيداً، نستخدم النزول الاشتقاقي كوسيلة لضبط النماذج.
التحدب
يساهم النزول الاشتقاقي بشكل عام بالتقليل من دالة الخسارة. كما اظهرنا ذلك في دالة Huber للخسارة، تكمن فائدة النزول الاشتقاقي عندما يكون صعب علينا إيجاد القيمة الدنيا.
اكتشاف الحدود الدنيا بالنزول الاشتقاقي
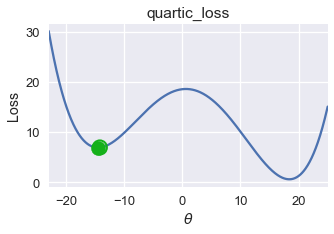
للأسف، في بعض الأحيان لا يمكن للنزول الاشتقاقي إيجاد قيمة $ \theta $. لنفترض التالي $ \theta = -21 $:
pts = np.array([0])
plot_loss(pts, (-23, 25), quartic_loss)
plot_theta_on_loss(pts, -21, quartic_loss)
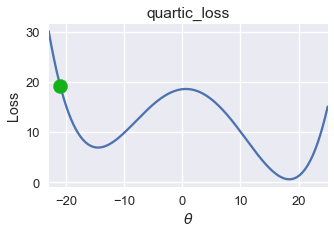
plot_one_gd_iter(pts, -21, quartic_loss, grad_quartic_loss)
old theta: -21
new theta: -9.944999999999999

plot_one_gd_iter(pts, -9.9, quartic_loss, grad_quartic_loss)
old theta: -9.9
new theta: -12.641412
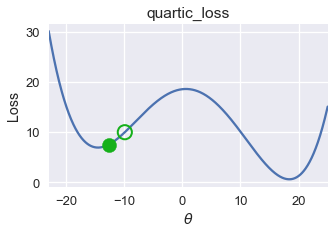
plot_one_gd_iter(pts, -12.6, quartic_loss, grad_quartic_loss)
old theta: -12.6
new theta: -14.162808
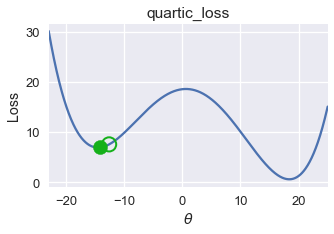
plot_one_gd_iter(pts, -14.2, quartic_loss, grad_quartic_loss)
old theta: -14.2
new theta: -14.497463999999999
في الأمثلة السابقة استخدم الكاتب الدوال التالية (دالة الخسارة الرباعية ونزولها الاشتقاقي) التي لم يعرفها مسبقاً:
def quartic_loss(theta, y_vals): return np.mean(1/5000 * (y_vals - theta + 12) * (y_vals - theta + 23) * (y_vals - theta - 14) * (y_vals - theta - 15) + 7) def grad_quartic_loss(theta, y_vals): return -1/2500 * (2 *(y_vals - theta)**3 + 9*(y_vals - theta)**2 - 529*(y_vals - theta) - 327)
في المثال السابق، دالة الخسارة الرباعية، كانت نتيجة النزول الاشتقاقي قريبه إلى $ \theta = -14.5 $، ولكن القيمة الدنيا العامة لدالة الخسارة هي $ \theta = 18 $، في هذا المثال نرى أن النزول الاشتقاقي يبحث عن القيمة الدنيا المحلية Local Minimum والتي ليست دائماً تساوي قيمة الخسارة للقيمة الدنيا العامة Global Minimum.
لحسن الحظ، بعض دوال الخسارة لديها نفس الرقم للقيمة الدنيا المحلية والعامة. لنأخذ مثلاً دالة الخطأ التربيعي المتوسط MSE:
pts = np.array([-2, -1, 1])
plot_loss(pts, (-5, 5), mse)
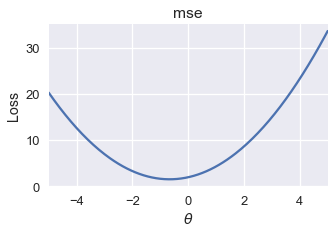
تطبيق النزول الاشتقاقي على هذه الدالة سيوجد لنا دائماً قيمه مثاليه عامه ل $ \theta $ كون القيمة الدنيا المحلية الوحيدة هي نفسها العامة.
متوسط الخطأ الحتمي قد يحتوي على أكثر من قيمه دنيا محلية. ولكن، كل القيم الدنيا هي نفسها القيمة الدنيا العامة.
pts = np.array([-1, 1])
plot_loss(pts, (-5, 5), abs_loss)
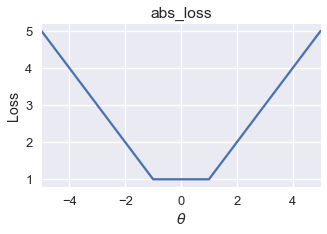
تعريف دالة متوسط الخطأ الحتمي
def abs_loss(theta, y_vals): return np.mean(np.abs(y_vals - theta))
في هذا المثال، ستكون قيمة النزول الاشتقاقي إحدى القيم المحلية الدنيا بين $ [-1, 1] $ كون أن كل القيم في هذا النطاق قيم دنيا لدالة الخسارة هذه، سيقترح النزول الاشتقاقي قيمة دنيا مثاليه بين هذه النقاط ل $ \theta $.
تعريف التحدب
في بعض الدوال، أي قيمه دنيا محلية هي نفسهاالعامه. هذه الدوال يطلق عليها دوال محدبة Convex function لأنها منحنية للأعلى. كذلك دالة Huber للخسارة، النموذج الثابت، MSE و MAE جميعها محدبة.
مع معدل تعلم Learning Rate مناسب، النزول الاشتقاقي يوجد $ \theta $ العامة المثالية لدالة الخسارة المحدبة. وبسبب ذلك، نفضل ضبط نماذجنا باستخدام الدوال المحدبة إلا إذا كان لدينا سبب مناسب غير ذلك.
بشكلٍ عام، الدالة $ f $ يطلق عليها دالة محدبة فقط إذا كانت توفي شروط المتباينة لجميع مدخلاتها $ a $ و $ b $ ، لكل $ t \in [0, 1] $: 📝
\[tf(a) + (1-t)f(b) \geq f(ta + (1-t)b)\]المتباينة تقول إن جميع الخطوط التي تربط نقطتين في الدالة يجب أن تقع على أو فوق الدالة. لدالة الخسارة التي عرضناها في بداية هذا الجزء، يمكننا إيجاد هذه الخط:
pts = np.array([0])
plot_loss(pts, (-23, 25), quartic_loss)
plot_connected_thetas(pts, -12, 12, quartic_loss)
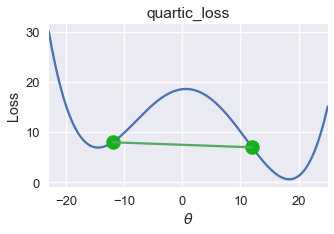
استخدم الكاتب الدالة plot_connected_thetas لتساعده على رسم الخط بين النقطتين، وعرفها الكاتب كالتالي:
def plot_connected_thetas(y_vals, theta_1, theta_2, loss_fn, **kwargs): plot_theta_on_loss(y_vals, theta_1, loss_fn) plot_theta_on_loss(y_vals, theta_2, loss_fn) loss_1 = loss_fn(theta_1, y_vals) loss_2 = loss_fn(theta_2, y_vals) plt.plot([theta_1, theta_2], [loss_1, loss_2])
وبناءًا على التعريف السابق، فهذه الدالة غير محدبة.
للخطأ التربيعي المتوسط، جميع الخطوط التي نقطتين تظهر فوق الرسم البياني. يمكننا رسم إحداها كالتالي:
pts = np.array([0])
plot_loss(pts, (-23, 25), mse)
plot_connected_thetas(pts, -12, 12, mse)
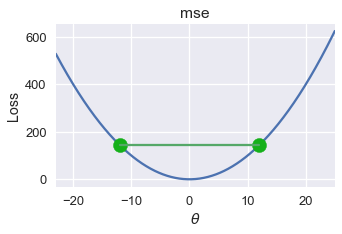
التعريف الرياضي للتحدب يعطينا وصف دقيق لتحديد ما اذا كانت الداله محدبه أو لا. في هذا الكتاب، سنتجاهل الجزء الرياضي لإثبات التحدب ونكتفي بالقول ما اذا كانت دالة محدبه أو لا.
ملخص التحدب
للداله المحدبه، أي قيمه دنيا محليه هي نفسها عامه. ذلك يسهل للنزول الاشتقاقي إيجاد افضل المتغيرات للنماذج لأي دالة خسارة. على الرغم من انه بإمكاننا استخدام النزول الاشتقاقي لدوال الخسارة غير المحدبه لإيجاد قيم دنيا، تلك القيم الدنيا المحليه غير مضمون أنها دائماً هي القيم العامه المثاليه.
النزول الاشتقاقي العشوائي
مقدمة
في هذا الجزء، سنتحدث عن تعديل على النزول الاشتقاقي يجعله أكثر فائدة للبيانات ذات الحجم الكبير. هذا التعديل يطلق عليه خوارزمية النزول الاشتقاقي العشوائي Stochastic Gradient Descent.
بعد أن تعلمنا طريقة عمل النزول الاشتقاقي وتحديثه لقيمة $ \theta $ باستخدام الاشتقاق لدالة الخسارة. بالذات استخدمنا المعادلة التالية:
\[{\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} L(\theta^{(t)}, \textbf{y})\]في هذه المعادلة:
- $ \theta^{(t)} $ هي التوقع الحالي ل $ \theta^{*} $ في التكرار $ t $.
- $ \alpha $ هي معدل التعلّم Learning Rate.
- $ \nabla_\theta L(\theta^{(t)}, \textbf{y}) $ هي اشتقاق دالة الخسارة.
- ونحسب التوقع التالي $ \theta^{(t+1)} $ عن طريق طرح $ \alpha $ و $ \nabla_\theta L(\theta, \textbf{y}) $ والمحسوبة في $ \theta^{(t)} $.
حدود النزول الاشتقاقي
في المعادلة السابقة، قمنا بحساب $ \nabla_\theta L(\theta, \textbf{y}) $ باستخدام متوسط الاشتقاق لدالة الخسارة $ \ell(\theta, y_i) $ لجميع البيانات. بمعنى آخر، في كل مرة نحدث قيمة $ \theta $ نتحقق من جميع النقاط الأخرى في بياناتنا. لهذا السبب، القانون للاشتقاق في المعادلة السابقة يطلق عليه النزول الاشتقاقي المُجَمع Batch Gradient Descent.
ولأننا لسوء الحظ عادة ما نعمل مع بيانات كبيرة الحجم، فإن النزول الاشتقاقي المُجَمع سيعمل لإيجاد القيمة المناسبة ل $ \theta $ بعد بضع تكرارات، ولكن كل تكرار قد يأخذ وقتاً طويل لحساب النتيجة فيه إذا كانت النقاط في بياناتنا كثيره.
النزول الاشتقاقي العشوائي
لحل مشكلة الوقت في حساب الاشتقاق لجميع بيانات التدريب، يقوم النزول الاشتقاقي العشوائي بتوقع القيمة باستخدام قيمه عشوائية واحدة من البيانات. ولأن القيمة تم اختيارها بشكل عشوائي، نتوقع أن الاشتقاق لكل نقطة سيؤدي بالنهاية إلى نفس النتيجة للنزول الاشتقاقي المُجَمع.
لنعود مرة أخرى لمعادلة النزول الاشتقاقي المُجَمع:
\[{\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} L(\theta^{(t)}, \textbf{y})\]في هذه المعادلة، لدينا المصطلح $ \nabla_{\theta} L(\theta^{(t)}, \textbf{y}) $، متوسط الاشتقاق لدالة الخسارة بين كل النقاط في بيانات التدريب، ومعادلتها:
\[\begin{aligned} \nabla_{\theta} L(\theta^{(t)}, \textbf{y}) &= \frac{1}{n} \sum_{i=1}^{n} \nabla_{\theta} \ell(\theta^{(t)}, y_i) \end{aligned}\]وفيها $ \ell(\theta, y_i) $ هي الخسارة في نقطة معينة في بيانات التدريب. لتطبيق النزول الاشتقاقي العشوائي، ببساطه نقوم بتغير متوسط الاشتقاق ب الاشتقاق في نقطة معينة. المعادلة بعد التعديل للنزول الاشتقاقي العشوائي هي:
\[{\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} \ell(\theta^{(t)}, y_i)\]في هذه المعادلة، $ y_i $ يتم اختيارها بشكل عشوائي من $ \textbf{y} $. لاحظ أن اختيار النقاط بشكل عشوائي مهم جداً لنجاح النزول الاشتقاقي العشوائي! إذا لم يتم اختيار النقاط بشكل عشوائي، قد ينتج لنا نتائج أسوأ من نتائج النزول الاشتقاقي المُجَمع.
نقوم عادةً باستخدام النزول الاشتقاقي العشوائي عن طريق خلط البيانات واستخدام كل نقطة بعد الخلط حتى تتجاوز أحد النقاط بيانات التدريب. إذا لم يتم ذلك، نعيد خلط النقاط والقيام بنفس الخطوات حتى تتجاوز البيانات. في كل تكرار Iteration النزول الاشتقاقي العشوائي يتحقق من نقطة واحده؛ وكل عملية تجاوز تتم بنجاح يطلق عليها Epoch.
استخدام دالة الخسارة MSE
كمثال، لنطبق النزول الاشتقاقي العشوائي على دالة الخسارة لMSE. لنتذكر تعريفها:
\[\begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2 \end{aligned}\]أخذ الاشتقاق $ \theta $ يصبح لدينا:
\[\begin{aligned} \nabla_{\theta} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \end{aligned}\]بما أن المعادلة السابقة تعطينا متوسط خسارة الاشتقاق لكل النقاط في البيانات، فإن خسارة الاشتقاق لنقطة معينة هي ببساطه جزء المعادلة التي تم أخذ متوسطه:
\[\begin{aligned} \nabla_{\theta} \ell(\theta, y_i) &= -2(y_i - \theta) \end{aligned}\]لتحديثها للاشتقاق المُجَمع لدالة الخسارة MSE:
\[\begin{aligned} {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \left( \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \right) \end{aligned}\]والنزول الاشتقاقي العشوائي لها سيكون كالتالي:
\[\begin{aligned} {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \left( -2(y_i - \theta) \right) \end{aligned}\]سلوك النزول الاشتقاقي العشوائي
بما أن الاشتقاق العشوائي فقط يتحقق من نقطة واحدة كل مرة، فإن تحديثه لقيمة $ \theta $ سيكون أقل دقه من التحديث إذا تم من النزول العشوائي المُجَمع. ولكن، بما أنه أسرع في حساب النتائج، فإن النزول الاشتقاقي العشوائي بإمكانه التقدم بشكل كبير للوصول للقيمة المناسبة ل $ \theta $ في حين النزول العشوائي المُجَمع لم ينتهي وقتها من التحديث ولا مرة واحدة. الصورة في الأسفل توضح تحديثات تمت بنجاح لقيمة $ \theta $ باستخدام النزول الاشتقاقي المُجَمع. المساحة غامقة اللون في الصوره تعني القيمة المثالية ل $ \theta $ على بيانات التدريب، وهي $ \hat{\theta} $. (الصورة تظهر نموذج لديه متغيران، ولكن من المهم ملاحظة طريقة النزول الاشتقاقي المُجَمع التي يصل فيها ل $ \hat{\theta} $.)
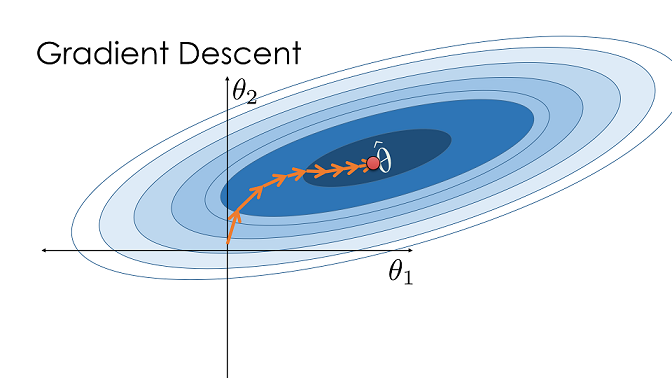
في الجانب الآخر، النزول الاشتقاقي العشوائي، عادة ما يأخذ خطوه بعيداً عن $ \hat{\theta} $، ولكن كونه يقوم بالتحديث بشكل متكرر، يصل غالباً للنقطة المثالية بشكل أسرع من المُجَمع.
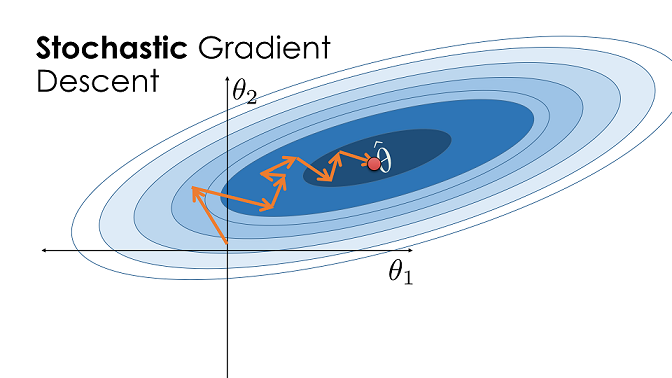
تعريف دالة للنزول الاشتقاقي العشوائي
كما فعلنا سابقاً، نقوم بتعريف دالة تحسب لنا النزول الاشتقاقي العشوائي لدالة خسارة. ستكون مشابهة لدالة minimize التي سبق تعريفها، ولكن نحتاج لإضافة الاختيار العشوائي للقيم في كل تكرار:
def minimize_sgd(loss_fn, grad_loss_fn, dataset, alpha=0.2):
"""
تستخدم النزول الاشتقاقي العشوائي للتقليل من دالة الخسارة loss_fn
تكون النتيجة القيمه الصغرى ل θ عندما يكون
الفرق بين التكرارات اقل من 0.001
"""
NUM_OBS = len(dataset)
theta = 0
np.random.shuffle(dataset)
while True:
for i in range(0, NUM_OBS, 1):
rand_obs = dataset[i]
gradient = grad_loss_fn(theta, rand_obs)
new_theta = theta - alpha * gradient
if abs(new_theta - theta) < 0.001:
return new_theta
theta = new_theta
np.random.shuffle(dataset)
نزول اشتقاقي بدفعات صغيرة
النزول الاشتقاقي بدفعات صغيرة Mini-batch Gradient Descent يحاول أن يوازن بين النزول الاشتقاقي العشوائي و المُجَمع عن طريقه زيادة عدد الأرقام التي يتطلع عليها في كل عملية تكرار. في النزول الاشتقاقي بدفعات صغيرة، نستخدم عدد من النقاط في كل تحديث بدلاً من نقطة واحدة. نستخدم متوسط الاشتقاق لدوال الخسارة للقيام بتوقع لقيمة الاشتقاق الصحيحة لخسارة الانتروبيا التقاطعية Cross Entropy Loss. إذا كانت $ \mathcal{B} $ هي الدفعة الصغيرة من النقاط التي نختارها بشكل عشوائي من $ n $، فالمعادلة الحالية كالتالي:
\[\nabla_\theta L(\theta, \textbf{y}) \approx \frac{1}{|\mathcal{B}|} \sum_{i\in\mathcal{B}}\nabla_{\theta}\ell(\theta, y_i)\]كما في النزول الاشتقاقي العشوائي، نقوم بالنزول الاشتقاقي بدفعات صغيرة عن طريق خلط بيانات التدريب واختيار دفعات عن طريق التكرار داخل البيانات المخلوطة. بعد كل Epoch، نعيد خلط البيانات واختيار دفعه صغيرة جديده.
على الرغم من أننا فرقنا بين النزول الاشتقاقي العشوائي وبدفعات صغيرة في هذه الكتاب، يستخدم مصطلح النزول الاشتقاقي العشوائي بشكل عام للاشتقاقات بدفعات صغيرة بأي حجم.
اختيار حجم الدفعات الصغيرة
يكون النزول الاشتقاقي بدفعات صغيرة مثالياً عندما يعمل على وحدة المعالجة الرسوميه GPU (كرت الشاشة للحاسب). كون العمليات من هذا النوع تأخذ وقتاً طويل، استخدام الدفعات الصغيرة يزيد من دقة الاشتقاق دون الزيادة من سرعة عملية الحساب. بناءًا على ذاكرة وحدة المعالجة الرسومية في الجهاز، يتم تحديد حجم الدفعات بين 10 و 100.
تعريف دالة للنزول الاشتقاقي بدفعات صغيرة
دالة النزول الاشتقاقي بدفعات صغيرة تحتاج لخيار لتحديد حجم الدفعات. الدالة التالية توفر هذه الخاصية:
def minimize_mini_batch(loss_fn, grad_loss_fn, dataset, minibatch_size, alpha=0.2):
"""
تستخدم النزول الاشتقاقي العشوائي بدفعات صغيره للتقليل من دالة الخسارة loss_fn
تكون النتيجة القيمه الصغرى ل θ عندما يكون
الفرق بين التكرارات اقل من 0.001
"""
NUM_OBS = len(dataset)
assert minibatch_size < NUM_OBS
theta = 0
np.random.shuffle(dataset)
while True:
for i in range(0, NUM_OBS, minibatch_size):
mini_batch = dataset[i:i+minibatch_size]
gradient = grad_loss_fn(theta, mini_batch)
new_theta = theta - alpha * gradient
if abs(new_theta - theta) < 0.001:
return new_theta
theta = new_theta
np.random.shuffle(dataset)
ملخص النزول الاشتقاقي العشوائي
نستخدم النزول الاشتقاقي بدفعات لتحسين النموذج بشكل متكرر حتى نصل إلى القيمة الدنيا للخسارة. بما أن النزول الاشتقاقي بدفعات يكون صعباً للحساب في البيانات الكبيرة، عادةً ما نستخدم النزول الاشتقاقي العشوائي لضبط تلك النماذج. عند استخدام GPU، النزول الاشتقاقي بدفعات بسيطه يمكنه الحساب بشكل أسرع من العشوائي بنفس تكلفة التشغيل. للبيانات الكبيرة، النزول الاشتقاقي العشوائي وبدفعات صغيرة هي أفضل للاستخدام كونها أسرع للحساب.