مبادئ وتقنيات علم البيانات
الفصل السابع عشر: التصنيف
فهرس الفصل:
مقدمة
حتى الآن ألقينا نظرة على نماذج للانحدار، طريقة للقيام بتوقعات مستمرة وبالأرقام بناءًا على البيانات. الآن ننتقل إلى التصنيف Classification، وهي طريقة للقيام بتوقعات تصنيفية بناءًا على البيانات. مثلاً، قنوات توقعات الطقس مهتمة بتوقع ما إذا سيكون غداً يوم ماطر أو غير ذلك بناءًا على حال الطقس اليوم.
معاً، التصنيف والانحدار تعتبر من النماذج الأولية والتي يَتَّجِه لها في التعليم الموجَّه Supervised Learning، والذي فيه يتعلم النموذج عن طريق تمرير البيانات ونتائجها عليه.
يمكننا إعادة تشكيل التصنيف على أنه نوع من أنواع الانحدار. بدلاً من أن نبني نموذج ليتوقع أرقام، ننشأ نموذج ليتوقع احتمالية أن قيمة من البيانات تنتمي لصنف ما. يسمح لنا ذلك بإعادة استخدام تقنيات الانحدار الخطي في الانحدار على الاحتمالات أو ما يسمى الانحدار اللوجستي Logistic Regression. 📝
الانحدار في الاحتمالات
في كرة السلة، تحسب نقاط المباريات عندما يقوم اللاعب بإدخال الكره في السلة. أحد اللاعبين، ليبرون جيمس، يعرف بأنه أحد أفضل من لعب كرة السلة بسبب قدراته في تسجيل النقاط.
.jpg)
يلعب ليبرون في الدوري الأمريكي لكرة السلة للمحترفين (NBA). قمنا بجمع جميع محاولات التسجيل لليبرون في المباريات الإقصائية لعام 2017 باستخدام موقع stats.nba.com.
لتحميل البيانات lebron.csv اضغط هنا.
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()
sns.set_context('talk')
np.set_printoptions(threshold=20, precision=2, suppress=True)
pd.options.display.max_rows = 7
pd.options.display.max_columns = 8
pd.set_option('precision', 2)
lebron = pd.read_csv('lebron.csv')
lebron
| shot_made | shot_distance | shot_type | action_type | opponent | minute | game_date | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 2PT Field Goal | Driving Layup Shot | IND | 10 | 20170415 | 0 |
| 1 | 0 | 2PT Field Goal | Driving Layup Shot | IND | 11 | 20170415 | 1 |
| 1 | 0 | 2PT Field Goal | Layup Shot | IND | 14 | 20170415 | 2 |
| … | … | … | … | … | … | … | … |
| 1 | 1 | 2PT Field Goal | Driving Layup Shot | GSW | 46 | 20170612 | 381 |
| 0 | 14 | 2PT Field Goal | Turnaround Fadeaway shot | GSW | 47 | 20170612 | 382 |
| 1 | 2 | 2PT Field Goal | Driving Layup Shot | GSW | 48 | 20170612 | 383 |
384 rows × 7 columns
كل سطر في هذه البيانات يحتوي على المعلومات التالية عن محاولات التسجيل لليبرون جيمس:
game_date: تاريخ المباراة.minute: الدقيقة التي حاول فيها التسجيل (مدة كل مباراة في كرة السلة الأمريكية 48 دقيقة).opponent: اختصار اسم الفريق المنافس.action_type: الطريقة التي تمت فيها محاولة التسجيل.shot_type: نوع الرمية (إما رمية نقطتين أو ثلاث نقاط).shot_distance: مسافة ليبرون عن السلة عندما قام بمحاولة التسجيل.shot_made: تكون 0 عندما تكون محاولة التسجيل فاشلة و 1 عندما تكون محاولة التسجيل ناجحة.
نريد أن نستخدم هذه البيانات لإجراء التوقعات عن احتمالية تسجيل ليبرون للمزيد من النقاط. تعتبر هذه مشكلة تصنيف Classification؛ نتوقع صِنف، وليس رقم كما نفعل في الانحدار>
يمكننا إعادة صياغة مشكلة التصنيف هذه إلى مشكلة انحدار نتوقع فيها الاحتمالية Probability إذا كانت الكرة ستدخل في السلة أم لا. مثلاً، نتوقع أن محاولات ليبرون للتسجيل ستخطأ السلة عندما تكون المحاولة من مسافة بعيدة.
نقوم برسم محاولات التسجيل، نظهر فيها المسافة عن السلة في المحور $ x $ و ما إذا تم تسجيل تلك المحاولة أو لا في المحور $ y $.
sns.lmplot(x='shot_distance', y='shot_made',
data=jitter_df(lebron, 'shot_distance', 'shot_made'),
fit_reg=False,
scatter_kws={'alpha': 0.3})
plt.title('LeBron Shot Make vs. Shot Distance');
إستخدم الكاتب الدالة
jutter_dfلتحويل البيانات إلى قيم عشوائية عن طريق إضافة قيمة عشوائية لها، وعرفها كالتالي:def jitter_df(df, x_col, y_col): x_jittered = df[x_col] + np.random.normal(scale=0, size=len(df)) y_jittered = df[y_col] + np.random.normal(scale=0.05, size=len(df)) return df.assign(**{x_col: x_jittered, y_col: y_jittered})
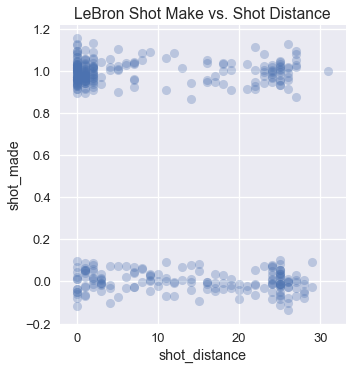
يمكن أن نرى أن ليبرون يسجل أكثر عندما يكون بحوالي 5 أقدام أو قل إلى السلة. عند ضبط نموذج بسيط للانحدار الخطي في المربعات الصغرى على هذه البيانات ينتج لنا التوقعات التالية:
sns.lmplot(x='shot_distance', y='shot_made',
data=jitter_df(lebron, 'shot_distance', 'shot_made'),
ci=None,
scatter_kws={'alpha': 0.4})
plt.title('Simple Linear Regression');
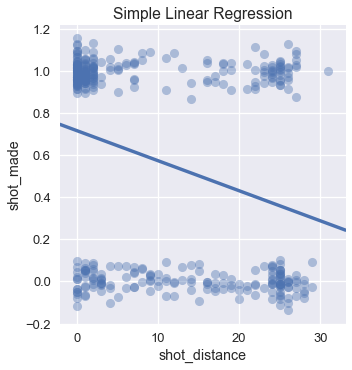
يستخدم الانحدار الخطي لتوقع قيم رقمية. ولكن عندما نريد تطبيقه على التصنيف، نريد تحويل هذه القيم الرقمية إلى تصنيف: تسجيل الكرة أو لا. يمكننا تطبيق ذلك عن طريق تحديد خط للقطع، أو حد فصل التصنيف Classification Threshold. إذا توقع الانحدار قيمة أكبر من 0.5، فيعني ذلك أن التوقع هو أن الكرة ستدخل السلة. على عكس ذلك، إذا توقع أقل من 0.5 فإن الكرة ستخطأ السلة.
رسمنا حد الفصل في الرسم البياني باللون الأخضر المتقطع. بناءًا على هذا الحد الفاصل، فإن نموذجنا يتوقع أن ليبرون سيجل الكرة إذا كان على بعد 15 قدم أو أقل عن السلة.
sns.lmplot(x='shot_distance', y='shot_made',
data=jitter_df(lebron, 'shot_distance', 'shot_made'),
ci=None,
scatter_kws={'alpha': 0.4})
plt.axhline(y=0.5, linestyle='--', c='g')
plt.title('Cutoff for Classification');
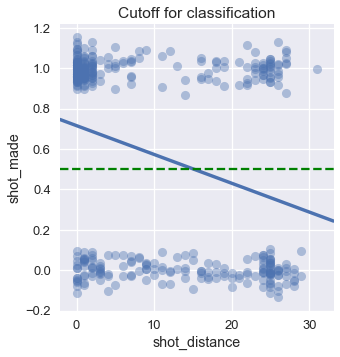
في الخطوات السابقة، حاولنا تطبيق الانحدار لتوقع احتمالية أن كرة ستصيب الهدف. إذا كان انحدارنا ينتج احتمالية، فإن تحديد الحد الفاصل على 0.5 يعني أننا نوقع أن الكرة ستصيب الهدف عندما يتوقع النموذج قيمة أعلى من ذلك. سنعود لموضوع حد فصل التصنيف في جزء آخر في هذا الفصل.
مشاكل الانحدار الخطي في الاحتمالات
للأسف، لا يمكننا اعتماد نتائج نموذجنا الخطي على أنها احتمالات. الاحتمالات الصحيحة يجب أن تكون بين 0 و 1، ولكن نموذجنا الخطي يخالف هذا الشرط. مثلاً، احتمالية أن يسجل ليبرون كرة من على بعد 100 قدم عن السلة يجب أن تكون أقرب إلى الصفر. ولكن، في حالتنا هنا، النموذج سيتوقع قيمة سلبية.
إذا قمنا بالتعديل على نموذجنا الخطي لتكون توقعاته عبارة عن احتمالات، لن نواجه مشكلة في استخدام توقعاته في التصنيف. يمكننا القيام بذلك باستخدام دالة توقع ودالة خسارة جديدة. يطلق على هذا النموذج بـ الانحدار اللوجستي Logistic Regression.
النموذج اللوجستي
في هذا الجزء، سنتعرف على الانحدار اللوجستي، نموذج خطي نستخدمة لتوقع الاحتمالات.
لنتذكر أن لضبط نموذج نحتاج لثلاث عناصر: نموذج يقوم بالتوقع، دالة خسارة، وطريقة لتحسين نتائج النموذج. سنستخدم النموذج الذي نعرفة الآن، الانحدار الخطي للمربعات الصغرى:
\[\begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) &= \hat{\boldsymbol{\theta}} \cdot \textbf{x} \end{aligned}\]ودالة الخسارة:
\[\begin{split} \begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_{i}(y_i - f_\boldsymbol{\theta} (\textbf{X}_i))^2\\ \end{aligned} \end{split}\]سنستخدم النزول الاشتقاقي كأداة لتحسين النتائج. في التعريف السابق، $ X $ تمثل مصفوفة البيانات $ n \times p $ (وفيها $ n $ هي عدد البيانات و $ p $ عدد العناصر / الأعمدة)، تمثل $ \textbf{x} $ سطر من $ X $، و $ y $ متّجه للنتائج التي سبق أن أطلع عليها. المتّجه $ \hat{\boldsymbol{\theta}} $ الوزن المثالي للنموذج و $ \boldsymbol{\theta} $ تمثل الوزن المتوسط الذي أنشئ أثناء محاولة تحسين النموذج.
الأعداد الحقيقية إلى احتمالات
لنرى أن نموذجنا $ f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \hat{\boldsymbol{\theta}} \cdot \textbf{x} $ يمكن أن يتوقع أي رقم حقيقي $ \mathbb{R} $ بما أنه ينتج مجموعة من الارقام خطية في $ \textbf{x} $، والتي بنفسها يمكن أن تحتوي على أي رقم من $ \mathbb{R} $.
يمكننا بسهله رسم ذلك بيانياً عندما تكون $ x $ رقم متدرج. إذا كانت $ \hat \theta = 0.5 $ فأن النموذج سيكون $ f_\hat{\theta} (\textbf{x}) = 0.5 x $. يمكن لتوقعات هذا النموذج أن تكون أي رقم من سالب مالا نهاية حتى موجب مالا نهاية:
xs = np.linspace(-100, 100, 100)
ys = 0.5 * xs
plt.plot(xs, ys)
plt.xlabel('$x$')
plt.ylabel(r'$f_\hat{\theta}(x)$')
plt.title(r'Model Predictions for $ \hat{\theta} = 0.5 $');
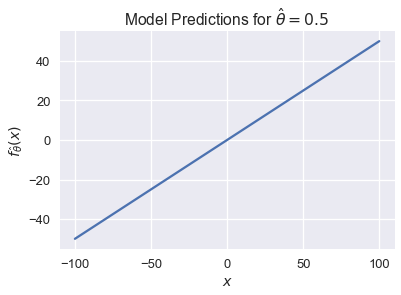
لمهام التصنيف، نريد تقييد $ f_\hat{\boldsymbol{\theta}}(\textbf{x}) $ بحيث تكون نتائجها عبارة عن احتمالية. يعني ذلك أن نتائجها تكون في المدى $ [0, 1] $ أيضاً، نريد أن تتطابق القيم الكبرى في $ f_\hat{\boldsymbol{\theta}}(\textbf{x}) $ مع قيم كبرى في الاحتمالية والعكس للقيم الصغرى مع قيمة احتمالية صغرى.
الدالة اللوجستية
لإنجاز ذلك، سنتعرف على الدالة اللوجستية Logistic Function، ويطلق عليها في بعض الأحيان الدالة السينية Sigmoid Function: 📝
\[\begin{aligned} \sigma(t) = \frac{1}{1 + e^{-t}} \end{aligned}\]لتسهيل القراءة، عادة ما نقوم بتغير $ e^x $ إلى $ \text{exp}(x) $:
\[\begin{aligned} \sigma (t) = \frac{1}{1 + \text{exp}(-t)} \end{aligned}\]قمنا برسم الدالة السينية للقيم التالية $ t \in [-10, 10] $:
from scipy.special import expit
xs = np.linspace(-10, 10, 100)
ys = expit(xs)
plt.plot(xs, ys)
plt.title(r'Sigmoid Function')
plt.xlabel('$ t $')
plt.ylabel(r'$ \sigma(t) $');
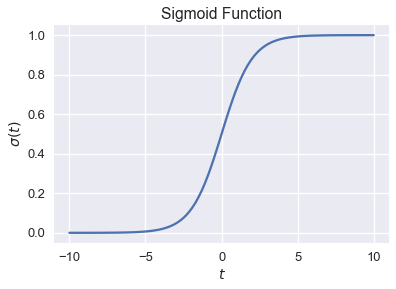
نلاحظ أن الدالة السينية $ \sigma(t) $ تأخذ رقم حقيقي $ \mathbb{R} $ وتكون نتائجها فقط أرقام بين 0 و 1. تقوم الدالة تدريجياً بالصعود بناءًا على القيم المدخلة $ t $؛ القيم الكبيرة في $ t $ هي القيم القريبة من 1، كما رغبناها أن تعمل. لم يتم ذلك بالصدفة؛ الدالة السينية يمكن اشتقاقها من نسبة لوغاريتميات الاحتمالات، ولكن قمنا بإخفاء الاشتقاق لتسهيل الشرح
تعريف النموذج اللوجستي
يمكننا الآن أخذ النموذج الخطي $ \hat{\boldsymbol{\theta}} \cdot \textbf{x} $ واستخدامه كمُدخل للدالة السينية لإنشاء النموذج اللوجستي:
\[\begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \sigma(\hat{\boldsymbol{\theta}} \cdot \textbf{x}) \end{aligned}\]بمعنى آخر، نأخذ نتيجة الانحدار الخطي، أي رقم حقيقي $ \mathbb{R} $، ونستخدمه في الدالة السينية لتقييد نتائج النموذج النهائية لتكون نتيجة احتمالية صحيح كرقم بين صفر وواحد.
لمعرفة طريقة عمل النموذج اللوجستي بشكل بسيط، سنقوم بتقييد قيمة $ x $ لتكون رقم متدرج ورسم نتيجة النموذج اللوجستي لعدة قيم لـ $ \hat{\theta} $:
# لا حاجة لفهم الكود البرمجي لأن الكاتب استخدمة لبناء الرسم البياني التوضيحي
def flatten(li): return [item for sub in li for item in sub]
thetas = [-2, -1, -0.5, 2, 1, 0.5]
xs = np.linspace(-10, 10, 100)
fig, axes = plt.subplots(2, 3, sharex=True, sharey=True, figsize=(10, 6))
for ax, theta in zip(flatten(axes), thetas):
ys = expit(theta * xs)
ax.plot(xs, ys)
ax.set_title(r'$ \hat{\theta} = $' + str(theta))
fig.add_subplot(111, frameon=False)
plt.tick_params(labelcolor='none', top='off', bottom='off',
left='off', right='off')
plt.grid(False)
plt.xlabel('$x$')
plt.ylabel(r'$ f_\hat{\theta}(x) $')
plt.tight_layout()
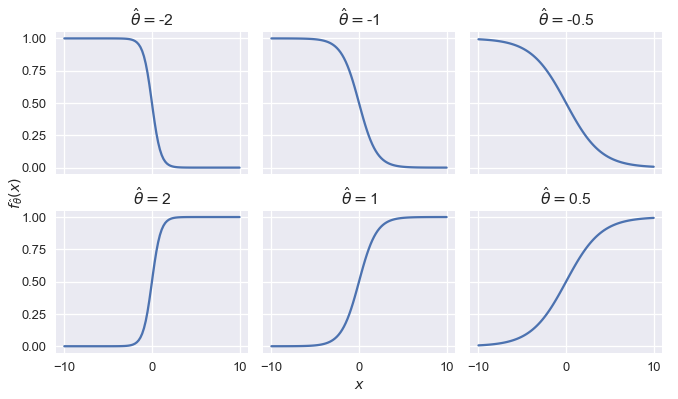
نلاحظ أن التغير في قيمة $ \hat{\theta} $ يغير من حِدة المنحنى؛ كلما أبعدنا عن $ 0 $، كلما زادت حدة المنحنى. تغير الإشارة في $ \hat{\theta} $ مع الإبقاء على نفس القيمة الرقمية ينتج لنا نفس النتائج لكن بشكل عكسي.
ملخص النموذج اللوجستي
تعرفنا على النموذج اللوجستي، طريقة جديدة للتوقع التي تُنتِج لنا توقعات كاحتمالات. لبناء النموذج، نستخدم مخرجات النموذج الخطي كمدخلات إلى الدالة اللوجستية غير الخطية.
دالة الخسارة للنموذج اللوجستي
قمنا بتعريف النموذج الخطي للاحتمالات، النموذج اللوجستي:
\[\begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \sigma(\hat{\boldsymbol{\theta}} \cdot \textbf{x}) \end{aligned}\]كما في النموذج الخطي، يحتوي النموذج على متغيرات $ \hat{\boldsymbol{\theta}} $، مصفوفة تحتوي على متغير واحد لكل خاصية في $ \textbf{x} $. سنقوم الآن بحل مشكلة تعريف دالة الخسارة لهذا النموذج والتي ستسمح لنا بضبط متغيرات النموذج لهذه البيانات.
ما نريده هو أن يقوم النموذج بتوقعات مطابقة بشكل كبير للبيانات. في الأسفل قمنا برسم بياني لمحاولات التسجيل لليبرون في المباريات الإقصائية لعام 2017 باستخدام بعد كُل تسديدة عن السلة:
sns.lmplot(x='shot_distance', y='shot_made',
data=lebron,
fit_reg=False, ci=False,
y_jitter=0.1,
scatter_kws={'alpha': 0.3})
plt.title('LeBron Shot Attempts')
plt.xlabel('Distance from Basket (ft)')
plt.ylabel('Shot Made');
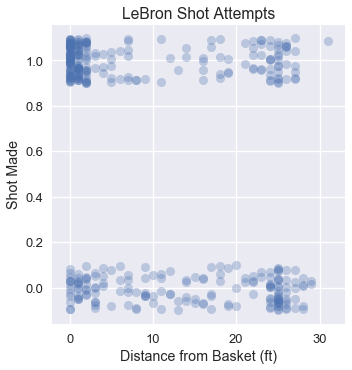
نلاحظ التجمع لكثير من المحاولات التي تم تسجيلها والتي كانت قريبة من السلة وتجمع قليل من البيانات لمحاولات تم تسجيلها من مسافات بعيدة عن السلة، نتوقع عندما نضبط النموذج اللوجستي على هذه البيانات أن النتيجة سيكون كالتالي:
from scipy.special import expit
sns.lmplot(x='shot_distance', y='shot_made',
data=lebron,
fit_reg=False, ci=False,
y_jitter=0.1,
scatter_kws={'alpha': 0.3})
xs = np.linspace(-2, 32, 100)
ys = expit(-0.15 * (xs - 15))
plt.plot(xs, ys, c='r', label='Logistic model')
plt.title('Possible logistic model fit')
plt.xlabel('Distance from Basket (ft)')
plt.ylabel('Shot Made');
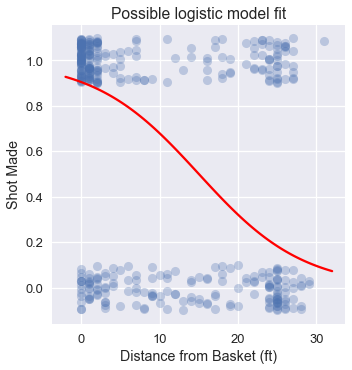
على الرغم أن بإمكاننا استخدام دالة خسارة الخطأ التربيعي المتوسط كما فعلنا في نموذج الانحدار الخطي، هي ليست ملائمة للنموذج اللوجستي ويصعب تحسين نتائجها.
خسارة الانتروبيا التقاطعية
بدلاً من الخطأ التربيعي المتوسط، سنستخدم خسارة الانتروبيا التقاطعية Cross-Entropy Loss. لتمثل $ \textbf{X} $ مصفوفة البيانات $ n \times p $، و $ \textbf{y} $ متّجه للنتائج التي سبق أن أطلع عليها، و $ f_\boldsymbol{\theta}(\textbf{x}) $ تمثل النموذج اللوجستي. تحتوي $ \boldsymbol{\theta} $ على قيم المتغيرات الحالية. باستخدام هذا التعريف، يمكننا تعريف معادلة متوسط خسارة الانتروبيا التقاطعية كالتالي: 📝
\[\begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = \frac{1}{n} \sum_i \left(- y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) \right) \end{aligned}\]يمكن أن تلاحظ، كما فعلنا مسبقاً، أننا أخذنا متوسط الخسارة لكل نقطة معينة في البيانات. ما في داخل التعريف السابق يمثل الخسارة لنقطة معينة $(\textbf{X}_i, y_i)$:
\[\begin{aligned} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i) = - y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) ) \end{aligned}\]لنتذكر أن كل قيمة $ y_i $ ستكون إما 0 أو 1. إذا كانت $ y_i = 0 $، فأول مصطلح في الخسارة يساوي صفر. إذا كانت $ y_i = 1 $، فأن ثاني مصطلح في التعريف السابق يساوي صفر. لذا، لكل نقطة في بياناتنا، فإن فقط جزء واحد من تعريف دالة خسارة الانتروبيا التقاطعية يساهم في حساب قيمة الخسارة النهاية.
لنفترض أن $ y_i = 0 $ والاحتمالية المتوقعة كانت $ f_\boldsymbol{\theta}(\textbf{X}_i) = 0 $، فإن نموذجنا كان توقعه صحيح. ستكون الخسارة لهذه النقطة كالتالي:
\[\begin{aligned} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i) &= - y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) ) \\ &= - 0 - (1 - 0) \ln (1 - 0 ) \\ &= - \ln (1) \\ &= 0 \end{aligned}\]كما هو متوقع، الخسارة للتوقع الصحيح هي $ 0 $. يمكنك التأكد من ذلك عندما تكون نتائج توقع الاحتماليه أبعد من القيمة الحقيقة، فإن الخسارة تكون عالية.
التقليل من خسارة الانتروبيا التقاطعية يحتاج أن يقوم النموذج $ f_\boldsymbol{\theta}(\textbf{x}) $ بأدق التوقعات الصحيحة الممكنة. لذلك، فإن دالة الخاسرة هذه مُحدبة، مما يجعل النزول الاشتقاقي مناسب لتحسين النتائج.
مشتقة خسارة الانتروبيا التقاطعية
لتطبيق النزول الاشتقاقي على خسارة الانتروبيا التقاطعية للنموذج يجب علينا حساب مشتقة الخسارة. أولاً، نقوم بحساب مشتقة الدالة السينية بما أننا سنستخدمها في عملية حساب الاشتقاق:
\[\begin{aligned} \sigma(t) &= \frac{1}{1 + e^{-t}} \\ \sigma'(t) &= \frac{e^{-t}}{(1 + e^{-t})^2} \\ \sigma'(t) &= \frac{1}{1 + e^{-t}} \cdot \left(1 - \frac{1}{1 + e^{-t}} \right) \\ \sigma'(t) &= \sigma(t) (1 - \sigma(t)) \end{aligned}\]يمكننا وصف مشتقة الدالة السينية من الدالة السينية نفسها.
للاختصار، نقوم بتعريف $ \sigma_i = f_\boldsymbol{\theta}(\textbf{X}_i) = \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) $. سنحتاج قريباً إلى مشتقة $ \sigma_i $ للمُتجهة $ \boldsymbol{\theta} $ لذا سنقوم بحسابة الآن باستخدام قاعدة السلسلة: 📝
\[\begin{aligned} \nabla_{\boldsymbol{\theta}} \sigma_i &= \nabla_{\boldsymbol{\theta}} \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) \\ &= \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) (1 - \sigma(\textbf{X}_i \cdot \boldsymbol{\theta})) \nabla_{\boldsymbol{\theta}} (\textbf{X}_i \cdot \boldsymbol{\theta}) \\ &= \sigma_i (1 - \sigma_i) \textbf{X}_i \end{aligned}\]والآن، سنوجد مشتقة خسارة الانتروبيا التقاطعية لمتغيرات النموذج $ \boldsymbol{\theta} $. في تفصيل حل المشتقة في الأسفل، جعلنا $ \sigma_i = f_\boldsymbol{\theta}(\textbf{X}_i) = \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) $:
\[\begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_i \left(- y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) \right) \\ &= \frac{1}{n} \sum_i \left(- y_i \ln \sigma_i - (1 - y_i) \ln (1 - \sigma_i) \right) \\ \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_i \left( - \frac{y_i}{\sigma_i} \nabla_{\boldsymbol{\theta}} \sigma_i + \frac{1 - y_i}{1 - \sigma_i} \nabla_{\boldsymbol{\theta}} \sigma_i \right) \\ &= - \frac{1}{n} \sum_i \left( \frac{y_i}{\sigma_i} - \frac{1 - y_i}{1 - \sigma_i} \right) \nabla_{\boldsymbol{\theta}} \sigma_i \\ &= - \frac{1}{n} \sum_i \left( \frac{y_i}{\sigma_i} - \frac{1 - y_i}{1 - \sigma_i} \right) \sigma_i (1 - \sigma_i) \textbf{X}_i \\ &= - \frac{1}{n} \sum_i \left( y_i - \sigma_i \right) \textbf{X}_i \\ \end{aligned}\]التعريف البسيط للمشتقة يسمح لنا بضبط النموذج اللوجستي لخسارة الانتروبيا التقاطعية باستخدام النزول الاشتقاقي:
\[\hat{\boldsymbol{\theta}} = \displaystyle\arg \min_{\substack{\boldsymbol{\theta}}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y})\]لاحقاً سنتعمق ونحدث في المعادلة لأنواع مختلفة من النزول الاشتقاقي الدُفعات، العشوائي والدفعات الصغيرة.
ملخص خسارة الانتروبيا التقاطعية
بما أن دالة خسارة الانتروبيا التقاطعية مُحدبة، نقوم بتقليلها باستخدام النزول الاشتقاقي لضبط النموذج اللوجستي على البيانات. لدينا الآن العناصر المهمة للانحدار اللوجستي: النموذج، دالة الخسارة وطريقة لتحسين النتائج. في جزء لاحق سنتعمق أكثر لمعرفة سبب استخدامنا لمتوسط خسارة الانتروبيا التقاطعية في الانحدار اللوجستي
استخدام الانحدار اللوجستي
تعرفنا على جميع العناصر المطلوبة في الانحدار اللوجستي، أولاً، النموذج اللوجستي المستخدم لإجراء توقعات الاحتماليات:
\[\begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \sigma(\hat{\boldsymbol{\theta}} \cdot \textbf{x}) \end{aligned}\]ثم دالة خسارة الانتروبيا التقاطعية:
\[\begin{split} \begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = &= \frac{1}{n} \sum_i \left(- y_i \ln \sigma_i - (1 - y_i) \ln (1 - \sigma_i ) \right) \\ \end{aligned} \end{split}\]وأخيراً، مشتقة خسارة الانتروبيا التقاطعية للنزول الاشتقاقي:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= - \frac{1}{n} \sum_i \left( y_i - \sigma_i \right) \textbf{X}_i \\ \end{aligned} \end{split}\]في المعادلة السالفة، جعلنا $ \textbf{X} $ تمثل مصفوفة البيانات $ n \times p $ ، تمثل $ \textbf{x} $ سطر من $ \textbf{X} $، و $ y $ متّجه للنتائج التي سبق أن أطلع عليها. و $ f_\hat{\boldsymbol{\theta}}(\textbf{x}) $ هي النموذج اللوجستي المثالي وذو متغيرات مثالية $ \hat{\boldsymbol{\theta}} $. للاختصار، نعرف $ \sigma_i = f_\hat{\boldsymbol{\theta}}(\textbf{X}_i) = \sigma(\textbf{X}_i \cdot \hat{\boldsymbol{\theta}}) $.
الانحدار اللوجستي على محاولات التسجيل لليبرون
لنعود للمشكلة التي واجهناها في بداية هذا الفصل: لنتوقع أي محاولات التسجيل لليبرون جيمس ستصيب الهدف. أولاً نحمل بيانات محاولات التصويب لليبرون في المباريات الإقصائية لعام 2017:
lebron = pd.read_csv('lebron.csv')
lebron
| shot_made | shot_distance | shot_type | action_type | opponent | minute | game_date | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 2PT Field Goal | Driving Layup Shot | IND | 10 | 20170415 | 0 |
| 1 | 0 | 2PT Field Goal | Driving Layup Shot | IND | 11 | 20170415 | 1 |
| 1 | 0 | 2PT Field Goal | Layup Shot | IND | 14 | 20170415 | 2 |
| … | … | … | … | … | … | … | … |
| 1 | 1 | 2PT Field Goal | Driving Layup Shot | GSW | 46 | 20170612 | 381 |
| 0 | 14 | 2PT Field Goal | Turnaround Fadeaway shot | GSW | 47 | 20170612 | 382 |
| 1 | 2 | 2PT Field Goal | Driving Layup Shot | GSW | 48 | 20170612 | 383 |
384 rows × 7 columns
لنلقي نظرة بشكل تفاعلي على هذه البيانات:
df_interact(lebron)

(384 rows, 7 columns) total
شُرحت هذه الدالة في فصل سابق ووظيفتها هي تمكين المستخدم من تصفح البيانات بشكل تفاعلي وتم تعريفها كالتالي:
%matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual def df_interact(df, nrows=7, ncols=7): def peek(row=0, col=0): return df.iloc[row:row + nrows, col:col + ncols] if len(df.columns) <= ncols: interact(peek, row=(0, len(df) - nrows, nrows), col=fixed(0)) else: interact(peek, row=(0, len(df) - nrows, nrows), col=(0, len(df.columns) - ncols)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1]))
نبدأ أولاً باستخدام مسافة محاولة التسجيل لتوقع ما إذا تم تسجيل المحاولة أم لا. توفر لنا مكتبة scikit-learn النموذج اللوجستي بشكل سهل عبر الكلاس sklearn.linear_model.LogisticRegression. لاستخدامه، نبدأ أولاً بإنشاء مصفوفة البيانات X، ومُتجهة النتائج التي المُطلع عليها y.
X = lebron[['shot_distance']].values
y = lebron['shot_made'].values
print('X:')
print(X)
print()
print('y:')
print(y)
X:
[[ 0]
[ 0]
[ 0]
...
[ 1]
[14]
[ 2]]
y:
[0 1 1 ... 1 0 1]
وكالمعتاد، سنقسم بياناتنا إلى بيانات تدريب و اختبار:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=40, random_state=42
)
print(f'Training set size: {len(y_train)}')
print(f'Test set size: {len(y_test)}')
Training set size: 344
Test set size: 40
تجعل مكتبة scikit-learn إنشاء وضبط النموذج على X_train و y_train عملية سهلة جداً:
from sklearn.linear_model import LogisticRegression
simple_clf = LogisticRegression()
simple_clf.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
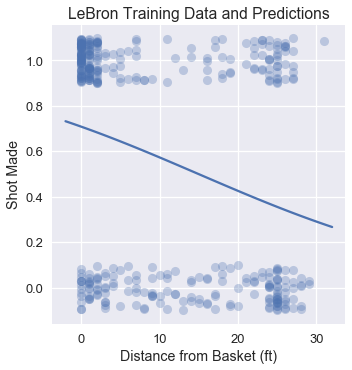
لعرض أداء النموذج في رسم بياني، سنتعرض النقاط الأصلية وتوقعات النموذج للاحتمالية:
sns.lmplot(x='shot_distance', y='shot_made',
data=lebron,
fit_reg=False, ci=False,
y_jitter=0.1,
scatter_kws={'alpha': 0.3})
xs = np.linspace(-2, 32, 100)
ys = simple_clf.predict_proba(xs.reshape(-1, 1))[:, 1]
plt.plot(xs, ys)
plt.title('LeBron Training Data and Predictions')
plt.xlabel('Distance from Basket (ft)')
plt.ylabel('Shot Made');
تقييم المصنف
إحدى الطرق لتقييم أداء النموذج هي بقياس دقة التوقعات: ما هي نسبة التوقعات الصحيحة؟
simple_clf.score(X_test, y_test)
0.6
يبدو أن أداء النموذج متدني قليلاً بدقة 0.6 على بيانات الاختبار. إذا قام نموذجنا بالتوقع على كل النقاط بشكل عشوائي، سنتوقع نتيجة الدقة ستكون 0.50. بالأصح، إذا قام نموذجنا ببساطة بتوقع كل محاولة لليبرون، سنحصل على نفس نسبة الدقة:
# حساب الدقة إذا كان التوقع 1
np.count_nonzero(y_test == 1) / len(y_test)
0.6
لهذا النموذج، استخدمنا متغير واحد من عدد مختلف من المتغيرات في هذه البيانات. في النموذج اللوجستي متعدد المتغيرات، سنحصل على نتائج أكثر دقة باستخدام أكثر من متغير.
نموذج لوجستي متعدد المتغيرات
الزيادة في عدد المتغيرات الرقمية في النموذج سهل جداً. على العكس، للمتغيرات من النوع النوعي/التصنيفية، نحتاج لتطبيق One-hot encoding. في الكود البرمجي التالي، أضفنا المزيد من المتغيرات للنموذج وهي minute، opponent، action_type و shot_type باستخدام كلاس DictVectorizer في مكتبة scikit-learn لتطبيق One-hot encoding على المتغيرات النوعية:
from sklearn.feature_extraction import DictVectorizer
columns = ['shot_distance', 'minute', 'action_type', 'shot_type', 'opponent']
rows = lebron[columns].to_dict(orient='row')
onehot = DictVectorizer(sparse=False).fit(rows)
X = onehot.transform(rows)
y = lebron['shot_made'].values
X.shape
(384, 42)
سنقوم مرة أخرى بتقسيم البيانات إلى بيانات تدريب و اختبار:
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=40, random_state=42
)
print(f'Training set size: {len(y_train)}')
print(f'Test set size: {len(y_test)}')
Training set size: 344
Test set size: 40
أخيراً، نقوم بضبط النموذج مرة أخرى ونتحقق من الدقة:
clf = LogisticRegression()
clf.fit(X_train, y_train)
print(f'Test set accuracy: {clf.score(X_test, y_test)}')
Test set accuracy: 0.725
دقة هذا النموذج أكثر بـ 12% من النموذج السابق الذي يستخدم متغير واحد. في جزء لاحق، سنستخدم مزيداً من الأدوات لتقييم أداء النموذج.
ملخص الانحدار اللوجستي
قمنا بتطوير عمليات حسابية رياضية وحاسوبية لاستخدام الانحدار اللوجستي في التصنيف. يستخدم الانحدار اللوجستي بشكل كبير لسهولته وفاعليته في التوقعات.
تقريب التوزيع الاحتمالي التجريبي
في هذا الجزء من الفصل، سنتعرف على تباعد KL (KL divergence) ونظهر كيف أن التقليل من متوسط التباعد KL في التصنيف ذو النتائج الثنائية (Binary 0/1) مماثل لاستخدام تقليل متوسط خسارة الانتروبيا التقاطعية. 📝
بما أن النتائج في الانحدار اللوجستي عبارة عن احتمالات، النموذج اللوجستي ينتج لنا نوعاً معين من توزيع الاحتمالات. بشكل خاص، بناءًا على المتغيرات المثالية $ \hat{\boldsymbol{\theta}} $، فأنه يقوم بتقييم احتمالية أن النتيجة $ y $ ستكون $ 1 $ لقيمة ادخلناها للنموذج $ \textbf{x} $.
مثلاً، لنفترض أن $ x $ قيمه رقمية تسجل احتمالية سقوط أمطار اليوم و $ y = 1 $ تعني أن السيد دو يحتاج لأخذ مظلته معه للعمل. النموذج اللوجستي ذو المتغيرات الرقمية $ \hat{\theta} $ يتوقع احتمالية إحتياج السيد دو لأخذ مظلته معه إلى العمل بناءًا على توقع سقوط الأمطار هذا اليوم: $ \hat{P_\theta}(y = 1 | x) $.
جمع بيانات استخدام السيد دو لمظلته يوفر لنا طريقة لبناء توزيع إحتمالي تجريبي $ P(y = 1 | x) $. مثلاً، إذا كان هناك خمس أيام كانت فيها احتمالية أن حالة الطقس ستكون ماطر هي $ x = 0.60 $ وقام السيد دو بأخذ مظلته مره واحدة، فأن $ P(y = 1 | x = 0.60) = 0.20 $. يمكننا حساب توزيع مماثل للاحتمالية لكل قيمة $ x $ تظهر في بياناتنا. بشكل طبيعي، بعد ضبط النموذج اللوجستي نريد ان تكون توقعات نموذجنا قريبة جداً إلى التوزيع الاحتمالي التجريبي في البيانات. يعني ذلك، لكل القيم $ x $ في البيانات، نريد:
\[\hat{P_\theta}(y = 1 \| x) \approx P(y = 1 | x)\]أحد طرق القياس الأكثر استخداماً لتحديد مدى قرب نتائج توزيعات الاحتمالان هو تباعد كولباك - ليبلير Kullback–Leibler divergence أو تباعد KL.
تعريف متوسط تباعد KL
يقوم تباعد KL بحساب الفرق بين توزيع احتمالية $ \hat{P_\boldsymbol{\theta}} $ التي قام بحسابها النموذج اللوجستي بالمتغيرات $ \boldsymbol{\theta} $ مع التوزيع الحقيقي للنقاط $ P $ في البيانات. يقوم بحساب مدى عدم دقة توقعات النموذج اللوجستي لتوزيعات البيانات.
تباعد KL لتصنيف ثنائي لتوزيعين $ P $ و $ \hat{P_\boldsymbol{\theta}} $ لنقطة واحدة $(\textbf{x}, y)$ هي:
\[D(P || \hat{P_\boldsymbol{\theta}}) = P(y = 0 | \textbf{x}) \ln \left(\frac{P(y = 0 | \textbf{x})}{\hat{P_\boldsymbol{\theta}}(y = 0 | \textbf{x})}\right) + P(y = 1 | \textbf{x}) \ln \left(\frac{P(y = 1 | \textbf{x})}{\hat{P_\boldsymbol{\theta}}(y = 1 | \textbf{x})}\right)\]تباعد KL ليس متناسق، مثلاً تباعد $ \hat{P_\boldsymbol{\theta}} $ عن $ P $ ليس نفس تباعد $ P $ عن $ \hat{P_\boldsymbol{\theta}} $:
\[D(P || \hat{P_\boldsymbol{\theta}}) \neq D(\hat{P_\boldsymbol{\theta}} || P)\]بما أن هدفنا هو استخدام $ \hat{P_\boldsymbol{\theta}} $ للتوقع التقريبي لـ $ P $، فنحن مهتمون بـ $ D(P \| \hat{P_\boldsymbol{\theta}}) $.
القيم المثالية لـ $ \boldsymbol{\theta} $، والتي أشرنا لها بـ $ \hat{\boldsymbol{\theta}} $، تقلل من متوسط تباعد KL لجميع نقاط البيانات $ n $:
\[\text{Average KL Divergence} = \frac{1}{n} \sum_{i=1}^{n} \left(P(y_i = 0 | \textbf{X}_i) \ln \left(\frac{P(y_i = 0 | \textbf{X}_i)}{\hat{P_\boldsymbol{\theta}}(y_i = 0 | \textbf{X}_i)}\right) + P(y_i = 1 | \textbf{X}_i) \ln \left(\frac{P(y_i = 1 | \textbf{X}_i)}{\hat{P_\boldsymbol{\theta}}(y_i = 1 | \textbf{X}_i)}\right)\right)\] \[\hat{\boldsymbol{\theta}} = \displaystyle\arg \min_{\substack{\boldsymbol{\theta}}} (\text{Average KL Divergence})\]في المعادلة السابقة، النقطة $i^{\text{th}} $ من نقاط البيانات أشير لها بـ ($ \textbf{X}_i $, $ y_i $) فيها $ \textbf{X}_i $ هي السطر $i^{\text{th}} $ من البيانات $n \times p$ في مصفوفة البيانات $ \textbf{X} $ و $ y_i $ هي النتائج التي سبق أن أطلع عليها.
لا يعاقب تباعد KL القيم الشاذة والنادر حدوثها في $ P $. إذا توقع النموذج احتمالية عالية لحدث نادر الحدوث، فإن كليهما $ P(k) $ و $ \ln \left(\frac{P(k)}{\hat{P_\boldsymbol{\theta}}(k)}\right) $ التباعد بينهما قليل. ولكن، إذا توقع النموذج احتمالية ضئيلة لحدث كثير الحدوث، فإن التباعد فيه عالي. يمكن أن نستنتج أن النموذج اللوجستي الذي يقوم بتوقعات صحيحة لأحداث كثيرة الحدوث لدية تباعد قليل من $ P $ على عكس نموذج يتوقع أحداث نادرة الحدود ولكن يختلف بشكل كبير في الأحداث كثيرة الحدوث.
استنتاج خسارة الانتروبيا التقاطعية من تباعد KL
تتشابه بشكل كبير المعادلة السابقة لتباعد KL مع خسارة الانتروبيا التقاطعية. سنعرض الآن في بعض العمليات الرياضية الجبرية أن تقليل متوسط تباعد KL يشابه تقليل متوسط خسارة الانتروبيا التقاطعية.
باستخدام خصائص اللوغاريتمات، يمكننا إعادة كتابة، يمكننا إعادة الكتابة كالتالي:
\[P(y_i = k | \textbf{X}_i) \ln \left(\frac{P(y_i = k | \textbf{X}_i)}{\hat{P_\boldsymbol{\theta}}(y_i = k | \textbf{X}_i)}\right) = P(y_i = k | \textbf{X}_i) \ln P(y_i = k | \textbf{X}_i) - P(y_i = k | \textbf{X}_i) \ln \hat{P_\boldsymbol{\theta}}(y_i = k | \textbf{X}_i)\]لاحظ بما أن المصطلح الأول لا يعتمد على $ \boldsymbol{\theta} $، فأنه لا يؤثر على $ \displaystyle\arg \min_{\substack{\boldsymbol{\theta}}} $ ويمكن حذفه من المعادلة. المعادلة الناتجة بعد ذلك حي خسارة الانتروبيا التقاطعية للنموذج $ \hat{P_\boldsymbol{\theta}} $:
\[\text{Average Cross-Entropy Loss} = \frac{1}{n} \sum_{i=1}^{n} - P(y_i = 0 | \textbf{X}_i) \ln \hat{P_\theta}(y_i = 0 | \textbf{X}_i) - P(y_i = 1 | \textbf{X}_i) \ln \hat{P_\theta}(y_i = 1 | \textbf{X}_i)\] \[\hat{\boldsymbol{\theta}} = \displaystyle\arg \min_{\substack{\theta}} (\text{Average Cross-Entropy Loss})\]بما أن $y_i$ هي قيمه معروفة، فإن احتمالية أن:
$y_i = 1$ و $P(y_i = 1 | \textbf{X}_i)$
تساوي
$ y_i $ و $P(y_i = 0 | \textbf{X}_i)$
هي $1 - y_i$.
توزيع احتماليات النموذج $ \hat{P_\boldsymbol{\theta}} $ معطاة من نتائج الدالة السينية التي سبق أن تعرفنا عليها في جزئية سابقة. بعد القيام بتلك التعويضات في المعادلة، نصل إلى معادلة متوسط خسارة الانتروبيا التقاطعية:
\[\text{Average Cross-Entropy Loss} = \frac{1}{n} \sum_i \left(- y_i \ln (f_\hat{\boldsymbol{\theta}}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\hat{\boldsymbol{\theta}}(\textbf{X}_i) \right)\] \[\hat{\boldsymbol{\theta}} = \displaystyle\arg \min_{\substack{\theta}} (\text{Average Cross-Entropy Loss})\]التبرير الإحصائي لخسارة الانتروبيا التقاطعية
لدى خسارة الانتروبيا التقاطعية أيضاً أسس أساسية في علم الإحصاء. بما أن الانحدار اللوجستي يتوقع احتمالات، لو سُلم لنا نموذج لوجستي يمكننا أن نسأل، “ما هي احتمالية أن هذا النموذج يكون لنا تلك المجموعة من البيانات التي سبق أن اطلع عليها $ y $؟” يمكننا بشكل طبيعي التعديل في المتغيرات للنموذج حتى تكون احتمالية حصولنا على بياناتنا كنتائج من النموذج عالية جداً. على الرغم من أننا لن نثبت ذلك في هذا الفصل، ولكن تطبيق ذلك مشابه للتقليل من خسارة الانتروبيا التقاطعية، هذا التفسير الإحصائي هو أقصى احتمال maximum likelihood لخسارة الانتروبيا التقاطعية.
ملخص تبرير خسارة الانتروبيا التقاطعية
يمكن القول ان متوسط تباعد KL هو متوسط الفرق اللوغارتمي بين توزيعان $ P $ و $ \hat{P_\boldsymbol{\theta}} $ تم وزنها باستخدام $ P $. التقليل من متوسط تباعد KL أيضاً يقلل من متوسط خسارة الانتروبيا التقاطعية. يمكننا التقليل من تباعد نموذج الانحدار اللوجستي عن طريق اختيار المتغيرات التي تصنف البيانات الشائعة بشكل صحيح.
ضبط النموذج اللوجستي
تحدثنا في جزء سابق عن النزول الاشتقاقي بدفعات Batch Gradient Descent، إحدى الخوارزميات التي تقوم بتحديث قيمة $ \boldsymbol{\theta} $ بشكل متكرر حتى قيمة المتغير $ \boldsymbol{\hat\theta} $ التي تقلل من الخسارة. و أيضاًً تحدثنا عن النزول الاشتقاقي العشوائي Stochastic Gradient Descent و النزول الاشتقاقي بدفعات صغيرة Mini-Batch Gradient Descent، كُلها طُرق تستفيد من النظرية الإحصائية والحوسبة المُتوازية للتقليل من الوقت لتدريب خوارزمية النزول الاشتقاقي. في هذا الجزء، سنطبق هذه المفاهيم في الانحدار اللوجستي ونأخذ أمثلة على ذلك باستخدام دوال مكتبة scikit-learn.
النزول الاشتقاقي بدفعات
دالة التحديث العامة في النزول الاشتقاقي بدفعات معطاة كالتالي:
\[\boldsymbol{\theta}^{(t+1)} = \boldsymbol{\theta}^{(t)} - \alpha \cdot \nabla_\boldsymbol{\theta} L(\boldsymbol{\theta}^{(t)}, \textbf{X}, \textbf{y})\]في الانحدار الخطي، نستخدم خسارة الانتروبيا التقاطعية كدالة خسارة:
\[L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = \frac{1}{n} \sum_{i=1}^{n} \left(-y_i \ln \left(f_{\boldsymbol{\theta}} \left(\textbf{X}_i \right) \right) - \left(1 - y_i \right) \ln \left(1 - f_{\boldsymbol{\theta}} \left(\textbf{X}_i \right) \right) \right)\]الاشتقاق لخسارة الانتروبيا التقاطعية هو \(\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = -\frac{1}{n}\sum_{i=1}^n(y_i - \sigma_i)\textbf{X}_i\) . تعويض ذلك في دالة التحديث يسمح لنا بإيجاد خوارزمية النزول الاشتقاقي الخاصة للانحدار اللوجستي. بجعل \(\sigma_i = f_\boldsymbol{\theta}(\textbf{X}_i) = \sigma(\textbf{X}_i \cdot \boldsymbol{\theta})\) :
\[\begin{align} \boldsymbol{\theta}^{(t+1)} &= \boldsymbol{\theta}^{(t)} - \alpha \cdot \left(- \frac{1}{n} \sum_{i=1}^{n} \left(y_i - \sigma_i\right) \textbf{X}_i \right) \\ &= \boldsymbol{\theta}^{(t)} + \alpha \cdot \left(\frac{1}{n} \sum_{i=1}^{n} \left(y_i - \sigma_i\right) \textbf{X}_i \right) \end{align}\]- $ \boldsymbol{\theta}^{(t)} $ هي القيمة الحالية المقدرة لـ $ \boldsymbol{\theta} $ في التكرار $t$.
- $ \alpha$ هي معدل التعلم.
- $-\frac{1}{n} \sum_{i=1}^{n} \left(y_i - \sigma_i\right) \textbf{X}_i$ هي مشتقة خسارة الانتروبيا التقاطعية.
- $ \boldsymbol{\theta}^{(t+1)} $ هي القيمة المقدرة التالية لـ $ \boldsymbol{\theta} $ والتي تم حسابها بطرح نتيجة ضرب $ \alpha$ و خسارة الانتروبيا التقاطعية التي تم حسابها في $ \boldsymbol{\theta}^{(t)} $.
النزول الاشتقاقي العشوائي
يقرب النزول الاشتقاقي العشوائي من مشتقة دالة الخسارة في جميع النقاط باستخدام مستشفى الخسارة لنقطة واحدة. دالة التحديث العامة كالتالي، وفيها $ \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i)$ هي دالة الخسارة لنقطة واحدة: 📝
\[\boldsymbol{\theta}^{(t+1)} = \boldsymbol{\theta}^{(t)} - \alpha \nabla_\boldsymbol{\theta} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i)\]بالعودة للمثال في الانحدار اللوجستي، نقوم بتقريب مشتقة خسارة الانتروبيا التقاطعية لجميع النقاط باستخدام خسارة الانتروبيا التقاطعية لنقطة واحدة. يظهر ذلك في المعادلة التالية، والتي فيها $ \sigma_i = f_{\boldsymbol{\theta}}(\textbf{X}_i) = \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) $:
\[\begin{align} \nabla_\boldsymbol{\theta} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &\approx \nabla_\boldsymbol{\theta} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i)\\ &= -(y_i - \sigma_i)\textbf{X}_i \end{align}\]عندما نقوم بتعويض التقريب إلى المعادلة العامة للنزول الاشتقاقي العشوائي، تتكون لنا دالة التحديث للنزول الاشتقاقي العشوائي للانحدار اللوجستي:
\[\begin{align} \boldsymbol{\theta}^{(t+1)} &= \boldsymbol{\theta}^{(t)} - \alpha \nabla_\boldsymbol{\theta} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i) \\ &= \boldsymbol{\theta}^{(t)} + \alpha \cdot (y_i - \sigma_i)\textbf{X}_i \end{align}\]النزول الاشتقاقي بدفعات صغيرة
بشكل مماثل، يمكننا تقريب مشتقة خسارة الانتروبيا التقاطعية لجميع النقاط باستخدام عينة عشوائية من البيانات، تعرف أيضاً بالدفعات الصغيرة. 📝
\[\nabla_\boldsymbol{\theta} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) \approx \frac{1}{|\mathcal{B}|} \sum_{i\in\mathcal{B}}\nabla_{\boldsymbol{\theta}} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i)\]نقوم بتعويض هذا التقريب لمشتقة خسارة الانتروبيا التقاطعية، ينتج عن ذلك دالة التحديث للنزول الاشتقاقي بدفعات صغيرة للانحدار اللوجستي:
\[\begin{align} \boldsymbol{\theta}^{(t+1)} &= \boldsymbol{\theta}^{(t)} - \alpha \cdot -\frac{1}{|\mathcal{B}|} \sum_{i\in\mathcal{B}}(y_i - \sigma_i)\textbf{X}_i \\ &= \boldsymbol{\theta}^{(t)} + \alpha \cdot \frac{1}{|\mathcal{B}|} \sum_{i\in\mathcal{B}}(y_i - \sigma_i)\textbf{X}_i \end{align}\]التطبيق في مكتبة Scikit-learn
الكلاس SGDClassifier في مكتبة scikit-learn يساعد على تنفيذ النزول الاشتقاقي العشوائي، يمكننا استخدامه بتحديد loss=log. بما أن scikit-learn لا تحتوي على نموذج لتطبيق النزول الاشتقاقي بدفعات صغيرة، سنقوم بمقارنة أداء SGDClassifier مع LogisticRegression على بيانات البريد الإلكتروني emails_sgd.csv. سنختصر جزئية اختيار الخصائص ولن نشرحها:
لتحميل البيانات emails_sgd.csv اضغط هنا.
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import SGDClassifier
# تحميل البيانات
emails = pd.read_csv('emails_sgd.csv').sample(frac=0.5)
# إختيار الخصائص ثم تحويلها لقيم رقمية
X, y = emails['email'], emails['spam']
X_tr = CountVectorizer().fit_transform(X)
# تقسيم البيناات لتدريب وإختبار
X_train, X_test, y_train, y_test = train_test_split(X_tr, y, random_state=42)
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
# ضبط النموذجان
log_reg = LogisticRegression(tol=0.0001, random_state=42)
stochastic_gd = SGDClassifier(tol=0.0001, loss='log', random_state=42)
%%time
from sklearn.metrics import accuracy_score, precision_score, recall_score
log_reg.fit(X_train, y_train)
log_reg_pred = log_reg.predict(X_test)
print('Logistic Regression')
print(' Accuracy: ', accuracy_score(y_test, log_reg_pred))
print(' Precision: ', precision_score(y_test, log_reg_pred))
print(' Recall: ', recall_score(y_test, log_reg_pred))
print()
Logistic Regression
Accuracy: 0.9913793103448276
Precision: 0.974169741697417
Recall: 0.9924812030075187
CPU times: user 3.2 s, sys: 0 ns, total: 3.2 s
Wall time: 3.26 s
%%time
stochastic_gd.fit(X_train, y_train)
stochastic_gd_pred = stochastic_gd.predict(X_test)
print('Stochastic GD')
print(' Accuracy: ', accuracy_score(y_test, stochastic_gd_pred))
print(' Precision: ', precision_score(y_test, stochastic_gd_pred))
print(' Recall: ', recall_score(y_test, stochastic_gd_pred))
print()
Stochastic GD
Accuracy: 0.9808429118773946
Precision: 0.9392857142857143
Recall: 0.9887218045112782
CPU times: user 93.8 ms, sys: 31.2 ms, total: 125 ms
Wall time: 119 ms
النتائج السابقة تظهر أن النموذج SGDClassifier استطاع إيجاد نتيجة في وقت أقل من LogisticRegression. على الرغم من أن نتائج تقييم النموذج SGDClassifier أسوأ قليلاً، إلا أننا نستطيع تحسين أداة النموذج SGDClassifier عبر ضبط الخصائص. أيضاً، هذه من المقايضات التي عادة ما يواجهها عالم البيانات. بناءًا على الوضع، يقوم عالم البيانات بإعطاء قيمة أعلى لسرعة إيجاد النتائج عن أداء
ملخص ضبط النموذج اللوجستي
يستخدم علماء البيانات النزول الاشتقاقي العشوائي للتقليل من تكلفة التشغيل والوقت. يمكننا مشاهدة ذلك في الانحدار اللوجستي، بما أن علينا فقط حساب مشتقة خسارة الانتروبيا التقاطعية لقيمة واحدة في كل تكرار بدلاً من كل القيم في النزول الاشتقاقي بدفعات. في المثال السابق عند استخدام scikit-learn والنموذج SGDClassifier، رأينا أن النزول الاشتقاقي العشوائي كانت نتائج أداءه أسوأ بعض الشيء، ولكن كأن أفضل من ناحية الوقت والسرعة بشكل كبير. في بيانات بحجم كبير و نماذج أكثر تعقيداً، الفرق في الوقت وسرعة إيجاد النتائج قد يكون أكبر بكثير وبذلك يكون أكثر أهمية.
تقييم النموذج اللوجستي
على الرغم من استخدامنا للدقة Accuracy لتقييم أداة النموذج اللوجستي في الجزء السابق، استخدام الدقة فقط يسبب بعض المشاكل التي سنتطرق لها في هذا الجزء من الفصل. للبدء في التحدث عن هذه المشاكل، سنتعرف على أداة أخرى لقياس أداء النموذج: المساحة أسفل المنحنى Area Under Curve (AUC). 📝
لنفترض أن لدينا بيانات 1000 بريد إلكتروني وتم تحديدها إذا كانت رسائل بريد مزعجة أم لا وهدفنا هو بناء نموذج ليفرق بين الرسائل الجديدة التي تصل لنا ما إذا كانت مزعجة أو لا. لنستعرض البيانات:
لتحميل البيانات selected_emails.csv اضغط هنا.
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
import pandas as pd
emails=pd.read_csv('selected_emails.csv', index_col=0)
emails
| spam | body | |
|---|---|---|
| 0 | \n Hi Folks,\n \n I’ve been trying to set a bu… | 0 |
| 0 | Hah. I guess she doesn’t want everyone to kno… | 1 |
| 0 | This article from NYTimes.com \n has been sent… | 2 |
| … | … | … |
| 1 | <html>\n <head>\n <meta http-equiv=”Conten… | 997 |
| 1 | <html>\n <head>\n </head>\n <body>\n \n <cente… | 998 |
| 1 | \n <html>\n \n <head>\n <meta http-equiv=3D”Co… | 999 |
1000 rows × 2 columns
كل سطر يحتوي على محتوى رسالة البريد الإلكتروني في العمود body وما إذا كانت رسالة البريد مزعجة أو لا في العمود spam، فيه 0 يعني أن الرسالة سليمة و 1 يعني أن الرسالة مُزعجة.
لنبدأ بتقييم أداء 3 نماذج مختلفة:
ham_only: يقيم كل رسالة بريد بأنها غير مزعجة “ham”.spam_only: يقيم كل رسالة بريد بأنها مزعجة “spam”.words_list_model: يتوقع الرسالة مزعجة أو لا بناءًا على توفر كلمات معينة في محتواها.
لنفترض أن لدينا مصفوفة للكلمات words_list نتوقع أنها تستخدم كثيراً في الرسائل المزعجة: “رجاءًا please”، “أضغط click”، “مال money”، “تجارة business”، و “حذف remove”. نبني نموذج words_list_model باستخدام الخطوات التالية: تحويل كل رسالة بريد إلى مصفوفة من الخصائص، بعد فصل الكلمات نحدد القيمة إلى 1 في حال وُجدت الكلمة في قائمة الكلمات words_list و 0 إذا لم تكن موجودة. مثلاً، عندما نستخدم الخمس كلمات السابقة وإذا وصلت لنا رسالة بريد إلكتروني محتواها “please remove by tomorrow”، فإن مصفوفة الخصائص الناتجة ستكون $ [1, 0, 0, 0, 1] $. تطبيق ذلك ينتج لنا مصفوفة خصائص $ \textbf{X} $ ذات حجم 1000 X 5.
الكود البرمجي التالي يظهر دقة النماذج. تم تجاهل شرح جزئية إنشاء النماذج وتدريبها للاختصار:
# تحديد كلمات الرسائل المزعجة
words_list = ['please', 'click', 'money', 'business', 'remove']
X = pd.DataFrame(words_in_texts(words_list, emails['body'].str.lower())).values
y = emails['spam'].values
# فصل البيانات لتدريب وإختبار
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=41, test_size=0.2
)
# ضبط النموذج
words_list_model = LogisticRegression(fit_intercept=True)
words_list_model.fit(X_train, y_train)
y_prediction_words_list = words_list_model.predict(X_test)
y_prediction_ham_only = np.zeros(len(y_test))
y_prediction_spam_only = np.ones(len(y_test))
print(f'ham_only test set accuracy: {np.round(accuracy_score(y_prediction_ham_only, y_test), 3)}')
print(f'spam_only test set accuracy: {np.round(accuracy_score(y_prediction_spam_only, y_test), 3)}')
print(f'words_list_model test set accuracy: {np.round(accuracy_score(y_prediction_words_list, y_test), 3)}')
ham_only test set accuracy: 0.96
spam_only test set accuracy: 0.04
words_list_model test set accuracy: 0.96
في المثال السابق، عرف الكاتب الدالة
words_in_textsوالتي تستقبل الكلمات والنص كمتغيرات على شكل مصفوفات، ونتيجتها مصفوفة من 0 و 1، 0 في حال لم تكن الكلمة موجودة في النص، و 1 في حال كانت موجودة:def words_in_texts(words, texts): indicator_array = np.array([texts.str.contains(word) * 1 for word in words]).T return indicator_array
النموذج words_list_model كان تصنيفه صحيح بنسبة 96% على بيانات الاختبار. على الرغم من أن الدقة لهذا النموذج تبدو عالية، إلا أن النموذج ham_only حصل على نفس النتيجة عن طريق تحديد كل الرسائل كرسائل غير مزعجة. يسبب ذلك بعض المشاكل لأن النتائج هذه توضح أن بإمكاننا الحصول على نفس النتائج دون استخدام نموذج وفلترة الرسائل.
كما تظهر نتائج الدقة السابقة، قد تضللنا بعض نتائج أداء النماذج. يمكننا التأكد من دقة توقعات النموذج بشكل أدق باستخدام مصفوفة الدقة Confusion Matrix. مصفوفة الدقة لنموذج ثنائي النتائج (0/1) هي خريطة حرارية heatmap ذات مقاسات 2×2 تحتوي على نتائج التوقعات في محور و النتائج الحقيقية في المحور الآخر.
كل قيمة في مصفوفة الدقة عبارة عن النتائج المحتملة للنموذج. إذا تم إدخال رسالة بريد إلكتروني مزعجة إلى النموذج، فإن لدينا احتمالان:
- True Positive (TP) (القيمة اليسار في الأعلى): توقع النموذج كان صحيح للرسالة بتحديدها كمزعجة.
- False Negative (FN) (القيمة اليمين في الأعلى): توقع النموذج كان خاطئ بتوقعها كرسالة غير مزعجة، كونها من المفترض أن يتم تصنيفها كرسالة مزعجة. في حالتنا، توقع خاطئ يعني أن رسالة مزعجة تم تحديدها كرسالة غير مزعجة ووصلت إلى صندوق بريدنا الرئيسي Inbox.
بنفس الطريقة، إذا تم إدخال رسالة بريد ألكتروني غير مزعجة إلى النموذج، سيكون لدينا احتمالان:
- False Positive (FP) (القيمة اليسار في الأسفل): توقع النموذج كان خاطئ بتحديد الرسالة كرسالة مزعجة وهي عكس ذلك كونها مصنفة كغير مزعجة. في حالتنا، هذا التصنيف يعني أن الرسالة ستصل إلى البريد المزعج في بريدنا الإلكتروني ولن تصل للبريد الرئيسي Inbox.
- True Negative (TN) (القيمة اليمين في الأسفل): توقع النموذج كان صحيح للرسالة بتحديدها كغير مزعجة.
سبق أن شرحت هذة المفاهيم في تدوينة على الرابط التالي: هنا، يمكن إختصار الشرح في الجدول التالي:
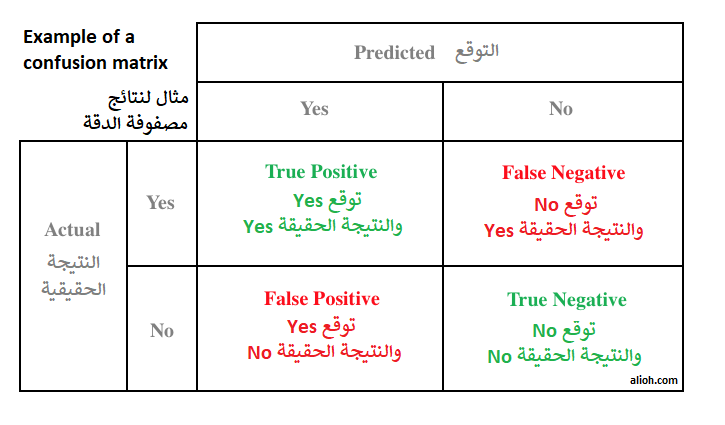
مع الاخذ بالإعتبار أن الشكل النهائي قد يختلف ويتم عكس الأعمدة Yes/No مثلاً.
تكلفة التوقع الخاطئ False Positive و False Negative تعتمد على ما نعمل عليه. في تصنيف رسائل البريد الإلكتروني، التصنيف الخاطئ False Positive يقوم بتحديد رسائل بريد إلكترونية مهمة كمزعجة وبالتالي يتم تجاهلها وعدم وضعها في البريد الرئيسي، لذا هي أسوأ من False Negative والذي فيه توضع الرسائل المزعجة في البريد الرئيسي. في المجال الطبي مثلاً، التوقع الخاطئ False Negative في تشخيص اختبار ما قد يكون أكثر أهمية من التوقع الخاطئ False Positive.
سنستخدم دالة مصفوفة الدقة Confusion Matrix في مكتبة scikit-learn لإنشاء مصفوفة الدقة للنماذج الثلاثة باستخدام بيانات التدريب. نتائج النموذج ham_only كالتالي:
from sklearn.metrics import confusion_matrix
class_names = ['Spam', 'Ham']
ham_only_cnf_matrix = confusion_matrix(y_train, ham_only_y_pred, labels=[1, 0])
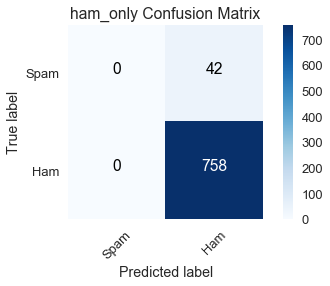
plot_confusion_matrix(ham_only_cnf_matrix, classes=class_names,
title='ham_only Confusion Matrix')
استخدم الكاتب الدالة
plot_confusion_matrixللمساعدة على الرسم والمتغيرham_only_y_predلتحديد جميع القيم كغير مزعجة وعرفهما كالتالي:def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues): """ ترسم هذه الدالة مصفوفة الدقة يمكن تبسيط النتائج باستخدام المتغير `normalize=True`. """ import itertools if normalize: cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] plt.imshow(cm, interpolation='nearest', cmap=cmap) plt.title(title) plt.colorbar() tick_marks = np.arange(len(classes)) plt.xticks(tick_marks, classes, rotation=45) plt.yticks(tick_marks, classes) fmt = '.2f' if normalize else 'd' thresh = cm.max() / 2. for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", color="white" if cm[i, j] > thresh else "black") plt.tight_layout() plt.ylabel('True label') plt.xlabel('Predicted label') plt.grid(False) ham_only_y_pred = np.zeros(len(y_train)) spam_only_y_pred = np.ones(len(y_train)) words_list_model_y_pred = words_list_model.predict(X_train)
لنجمع من الرسم البياني السابق مجموع النتائج في الصفوف لبيانات التدريب ونرى إذا تم تصنيفها في التصنيف الذي تنتمي إليه:
- True label = spam (السطر الأول): مجموع الرسائل التي تم توقعها كمزعجة وهي فعلاً مزعجة True Positive (0)، والنتائج التي تم توقعها كغير مزعجة وهي في الحقيقة مزعجة False Negative (42)، يظهر لذلك أن هناك 42 رسالة بريد إلكتروني مزعجة في بيانات التدريب.
- True label = ham (السطر الثاني): مجموع الرسائل التي توقعها كمزعجة وهي في الحقيقة غير مزعجة False Positive (0)، ويليها توقعات الرسائل التي كانت غير مزعجة وهي فعلاً غير مزعجة True Negative (758)، يعني ذلك أن هناك 758 رسالة بريد غير مزعجة في بيانات التدريب.
لنجمع من الرسم البياني السابق مجموع النتائج في الأعمدة لبيانات التدريب ونرى أداء النموذج في توقع تصنيفها الذي تنتمي إليه:
- Predicted label = spam (العمود الأول): مجموع توقعات الرسائل التي تم توقعها كمزعجة وهي فعلاً مزعجة True Positive (0)، مجموع توقعات الرسائل التي توقعها كمزعجة وهي في الحقيقة غير مزعجة False Positive (0) يظهر أن توقعات
ham_onlyأنه لا يوجد أي رسالة بريد إلكتروني مزعجة في بيانات التدريب. - Predicted label = ham (العمود الثاني): مجموع التوقعات التي تم توقعها كغير مزعجة وهي في الحقيقة مزعجة False Negative (42)، مجموع توقعات الرسائل التي كانت غير مزعجة وهي فعلاً غير مزعجة True Negative (758) يظهر أن توقعات
ham_onlyأن هناك 800 رسالة بريد إلكتروني غير مزعجة في بيانات التدريب.
نرى أن النموذج ham_only لدية دقة عالية $ \left(\frac{758}{800} \approx .95\right) $ لأن هناك 758 رسالة بريد إلكتروني غير مزعجة في بيانات التدريب من أصل 800.
spam_only_cnf_matrix = confusion_matrix(y_train, spam_only_y_pred, labels=[1, 0])
plot_confusion_matrix(spam_only_cnf_matrix, classes=class_names,
title='spam_only Confusion Matrix')
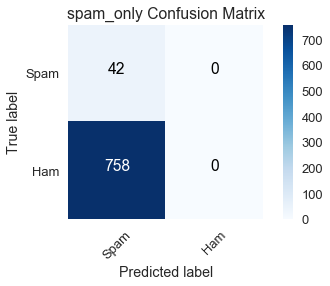
في الجانب الآخر، النموذج spam_only كانت توقعاته أن بيانات التدريب لا تحتوي على أي رسالة بريد إلكتروني غير مزعجة ham، وكما هو واضح في مصفوفة الدقة النتيجة أبعد ما تكون عن الحقيقة والتي فيها 758 رسالة بريد إلكتروني غير مزعجة.
لنلقي نظرة على النموذج الذي يهمنا words_list_model ونتيجة مصفوفة الدقة:
words_list_model_cnf_matrix = confusion_matrix(y_train, words_list_model_y_pred, labels=[1, 0])
plot_confusion_matrix(words_list_model_cnf_matrix, classes=class_names,
title='words_list_model Confusion Matrix')
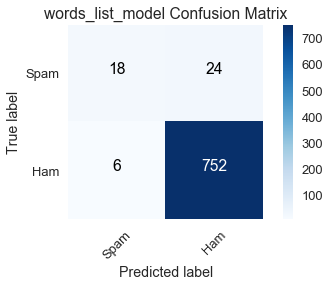
مجموع الصفوف مطابق لتلك في النتائج في مصفوفات الدقة للنماذج ham_only و spam_only كما هو متوقع لأن النتائج الحقيقية للمجموع في بيانات التدريب لن تتغير مهما تغير النموذج.
من بين ال 42 رسالة بريد مزعج، توقع النموذج words_list_model بشكل صحيح 18 رسالة، وهذا أداء سيئ. دقته العالية كانت بسبب العدد الكبير المتوقع للنتائج الصحيحة للرسائل الغير مزعجة True Negative، يعتبر ذلك غير كافٍ لأنه لا يفي بالغرض في فلترة رسائل البريد المزعجة.
بيانات رسائل البريد الإلكتروني هي مثال على بيانات ذات تصنيف غير المتوازن Class-imbalanced dataset، فيها الكثير من التصنيفات تنتمي لتصنيف أكثر من الآخر. في حالة بيانات البريد الإلكتروني، فإن الكثير من الرسائل تم تصنيفها كغير مزعجة. مثال آخر منتشر هو في بيانات اكتشاف الأمراض عندما يكون انتشار المرض في المجتمع الإحصائي قليل. نسبة الحصول على نتيجة أن المريض ليس لدية المرض عند إجراء الفحص الطبي أعلى سبب أن الكثير من المرضى ليس لديهم المرض، عدم قدرته على كشف المرضى بذلك المرض يظهر عدم فائدة النموذج. 📝
ننتقل الآن إلى الحساسية والنوعية، طرق قياس مناسبة للبيانات ذات التصنيف غير المتوازن.
الحساسية
تسمى الحساسية Sensitivity أيضاً بـ معدل التوقع والنتيجة الإيجابيان True Positive Rate يقيس نسبة البيانات التي تنتمي إلى التصنيف الإيجابي وتوقعها النموذج بشكل صحيح: 📝
\[\text{Sensitivity} = \frac{TP}{TP + FN}\]في حديثنا السابق عن مصفوفات الدقة، فيجب عليك الآن أن تكون قد تعرفت على المصطلحات $TP + FN$ وهي مجموع القيم في الصف الأول، وهي تساوي المجموع الحقيقي للبيانات التي تنتمي للتصنيف الإيجابي Positive Class. استخدام مصفوفات الدقة يسهل علينا مقارنة الحساسية في النماذج:
ham_only: $ \frac{0}{0 + 42} = 0$spam_only: $ \frac{42}{42 + 0} = 1$words_list_model: $ \frac{18}{18 + 24} \approx .429$
بما أن النموذج ham_only لم يكون فيه أي قيمه صحيحة في العمود True Positive، فحصل على أسوأ النتائج 0 في الحساسية. على الجانب الآخر، النموذج spam_only كانت الدقة فيه قليلة جداً إلا انه حسب على أفضل النتائج في الحساسية 1 لأنه توقع جميع رسائل البريد المزعجة بشكل صحيح. النتيجة المتدنية للنموذج words_list_model تعني أنه عادة ما يفشل في توقع رسائل البريد الإلكتروني كمزعجة؛ ولكن على العكس، النموذج أفضل بكثير من النموذج ham_only.
النوعية
تسمى النوعية Specificity أيضاً بـ معدل التوقع والنتيجة السلبيان True Negative Rate يقيس نسبة البيانات التي تنتمي إلى التصنيف السلبي وتوقعها النموذج بشكل صحيح: 📝
\[\text{Specificity} = \frac{TN}{TN + FP}\]المصطلح $TN + FP$ يساوي المجموع الحقيقي للبيانات التي تنتمي للتصنيف السلبي Negative Class. مرة أخرى، استخدام مصفوفات الدقة يسهل علينا مقارنة النوعية في النماذج:
ham_only: $ \frac{758}{758 + 0} = 1$spam_only: $ \frac{0}{0 + 758} = 0$words_list_model: $ \frac{752}{752 + 6} \approx .992$
كما في الحساسية، النتائج من 0 إلى 1 من الأسوأ إلى الأفضل. لاحظ أن ham_only حصل على أفضل النتائج في النوعية و أسوأ النتائج في الحساسية، بينما spam_only حصل على أسوأ النتائج في النوعية والأفضل في الحساسية. بما أن هذه النماذج تتوقع نتيجة واحدة فقط، فأنها تصنف جميع القيم من التصنيف الآخر بشكل خاطئ، يظهر ذلك في القيم العالية للنوعية والحساسية. الفرق في النتائج في النموذج words_list_model أقل.
على الرغم أن الحساسية والتصنيف تعرفنا على خصائص مختلفة في النموذج، نحتاج أن نربط تلك النتائج في أداتا التقييم مع بعضها البعض باستخدام حد فصل التصنيف
حد فصل التصنيف
قيمة حد فصل التصنيف Classification Threshold تحدد إي تصنيف تنتمي إليه قيمة ما؛ القيم على الجانبين المختلفين من حد الفصل يتم يختلف تصنيفها عن بعضها. لنتذكر أن النتائج في الانحدار اللوجستي عبارة عن احتماليات إذا كانت النقطة تنتمي إلى التصنيف الإيجابي. إذا كانت الاحتمالية أكبر من حد الفصل، فأنها تنتمي إلى التصنيف الإيجابي، إذا كانت أقل من حد الفصل، فأنها تنتمي إلى التصنيف السلبي. في مثالنا، لنجعل $f_{\hat{\theta}} $ نموذجنا اللوجستي و $ C $ هو حد الفصل. إذا كانت $f_{\hat{\theta}}(x) > C$، فإن $x$ تصنف رسالة بريد مزعج؛ إذا كانت $f_{\hat{\theta}}(x) < C$، فإن $ x $ تصنف كرسالة غير مزعجة. تفصل مكتبة scikit-learn عند تعادل النتيجة مع حد الفصل للتصنيف السلبي، إذاً عندما تكون $f_{\hat{\theta}}(x) = C$، فإن $ x $ يتم تصنيفها كرسالة غير مزعجة. 📝
يمكننا تقييم أداء النموذج مع حد الفصل $ C $ باستخدام مصفوفة الدقة. مصفوفة الدقة للنموذج words_list_model التي سبق أن عرضناها تستخدم القيمة الافتراضية لحد الفصل في مكتبة scikit learn وهي $C = .50$.
الرفع من حد الفصل إلى $C = .70$، يعني أننا نصنف رسالة البريد الإلكتروني $ x $ كمزعجة عندما تكون الاحتمالية $f_{\hat{\theta}}(x)$ أعلى من $ .70 $، النتائج لمصفوفة الدقة عندما يكون حد الفصل $.70 $ كالتالي:
# إيجاد احتماليات التوقع
words_list_prediction_probabilities = words_list_model.predict_proba(X_train)[:, 1]
# عندما تكون الاحتمالية أكبر من .70 محدد رسالة البريد كرسالة مزعجة، والعكس غير ذلك
words_list_predictions = [1 if pred >= .70 else 0 for pred in words_list_prediction_probabilities]
# إنشاء مصفوفة الدقة
high_classification_threshold = confusion_matrix(y_train, words_list_predictions, labels=[1, 0])
# رسم مصفوفة الدقة
plot_confusion_matrix(high_classification_threshold, classes=class_names,
title='words_list_model Confusion Matrix $C = .70$')
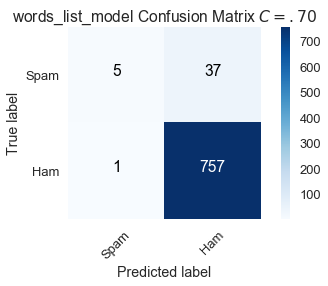
عند رفع حد الفصل لتحديد ما إذا كانت رسالة البريد الإلكتروني مزعجة أم لا، يوجد 13 رسالة بريد مزعجة تم تحديدها بشكل صحيح عندما كانت $C = 0.50$ والآن هي مصنفة بشكل خطأ:
\[\text{Sensitivity } (C = .70) = \frac{5}{42} \approx .119 \\ \text{Specificity } (C = .70) = \frac{757}{758} \approx .999\]عند المقارنة بالقيمة الافتراضية، قيمة حد فصل أعلى عند $C = .70$ تزيد من النوعية وتقلل من الحساسية.
التقليل من حد الفصل إلى $C = .30$، يعني أن أي رسالة بريد إلكتروني $ x $ تصنف كمزعجة عندما تكون الاحتمالية $f_{\hat{\theta}}(x)$ أكبر من $ .30 $، نتيجة مصفوفة الدقة كالتالي:
# عندما تكون الاحتمالية أكبر من .30 محدد رسالة البريد كرسالة مزعجة، والعكس غير ذلك
words_list_predictions = [1 if pred >= .30 else 0 for pred in words_list_prediction_probabilities]
# إنشاء مصفوفة الدقة
low_classification_threshold = confusion_matrix(y_train, words_list_predictions, labels=[1, 0])
# رسم مصفوفة الدقة
plot_confusion_matrix(low_classification_threshold, classes=class_names,
title='words_list_model Confusion Matrix $C = .30$')
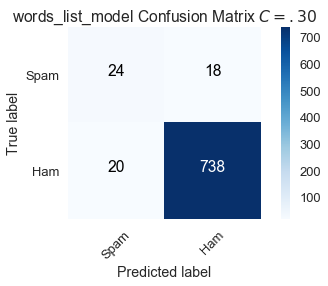
عند التقليل من حد الفصل لرسائل البريد الإلكتروني المزعجة، تم تصنيف 6 رسائل بريد إلكتروني مزعجة كانت مصنفة بشكل خاطئ عندما كانت $C = .50$ وهي الآن مصنفة بشكل صحيح. ولكن، هناك عدد أكبر من القيم السلبية في الحقيقة وتم توقعها إيجابياً False Positive:
\[\begin{split} \text{Sensitivity } (C = .30) = \frac{24}{42} \approx .571 \\ \text{Specificity } (C = .30) = \frac{738}{758} \approx .974 \end{split}\]بالمقارنة مع القيمة الافتراضية، حد فصل أقل عند $C = .30$ زاد من الحساسية وقلل من النوعية.
نقوم بالتعديل من نتائج الحساسية والنوعية للنموذج عن طريق تعديل حد الفصل. على الرغم أننا نرغب في الحصول على أفضل النتائج في الحساسية والنوعية، يمكن أن نرى من مصفوفات الدقة بحدود فصل مختلفة أن هناك مقايضة تحدث. الزيادة في الحساسية تؤدي إلى النقص في النوعية والعكس.
منحنيات ROC
يمكننا حساب الحساسية والنوعية أيًّا كانت قيمة حد الفصل بين 0 و 1 ورسمها. كل قيمة لحد الفصل $ C $ مرتبطة بالحساسية والنوعية معًا. منحنى خصائص تشغيل المُستقْبِل ROC (Receiver Operating Characteristic) Curve يختلف بعض الشيء؛ بدلاً من رسم النقطة (الحساسية ،النوعية)، يرسم (الحساسية، 1-النوعية)، وفيها 1-النوعية معرفة بمعدل القيم السلبية التي تم توقعها إيجابياً False Positive: 📝
\[\text{False Positive Rate } = 1 - \frac{TN}{TN + FP} = \frac{TN + FP - TN}{TN + FP} = \frac{FP}{TN + FP}\]نقطة في منحنى ROC تمثل الحساسية ومعدل القيم السلبية التي تم توقعها إيجابياً False Positive المرتبطة بقيمة حد الفصل.
منحنى ROC لنموذج words_list_model يمكن حسابها باستخدام دالة منحنى ROC في مكتبة scikit-learn:
from sklearn.metrics import roc_curve
words_list_model_probabilities = words_list_model.predict_proba(X_train)[:, 1]
false_positive_rate_values, sensitivity_values, thresholds = roc_curve(y_train, words_list_model_probabilities, pos_label=1)
plt.step(false_positive_rate_values, sensitivity_values, color='b', alpha=0.2,
where='post')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('Sensitivity')
plt.title('words_list_model ROC Curve')
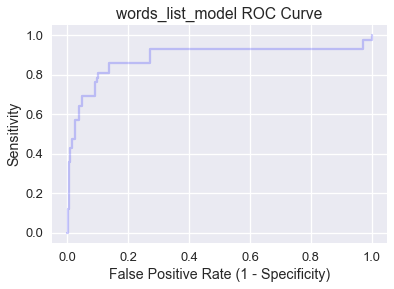
لاحظ أننا كُلما انتقلنا من اليسار إلى اليمين عبر المنحنى، تزيد الحساسية وتقل النوعية. بشكل عام، أفضل حد للفصل تتفاعل عندما تتكون الحساسية والنوعية عالية (قيمة أقل لمعدل القيم السلبية التي تم توقعها إيجابياً False Positive)، لذا النقاط في الأعلى يساراً هي النقاط المثالية.
لننظر بشكل أكبر للزوايا الأربعة في الرسم البياني السابق:
- (0, 0): النوعية $ 1 = $، يعني أن جميع البيانات في التصنيف السلبي تم تصنيفها بشكل صحيح، ولكن الحساسية $ 0 = $، إذاً النموذج لا يحتوي على قيم إيجابية وتم توقعها إيجابياً True Positive. حد الفصل عند النقطة (0, 0) فيه $ C = 1.0 $، وهو مطابق لنتائج النموذج
ham_onlyبما أنه لا يمكن لأي رسالة بريد إلكتروني أن تحصل على احتمالية أعلى من $ 1.0 $. - (1, 1): النوعية $ 0 = $، يعني أن النموذج لا يحتوي توقعات سلبية وتم توقعها سلبياً True Negative، ولكن الحساسية $ 1 = $، يعني أن جميع البيانات في التصنيف الإيجابي تم تصنيفها بشكل صحيح. الفصل عند النقطة (1, 1) فيه $ C = 0.0 $، وهو مطابق لنتائج النموذج
spam_onlyبما أنه لا يمكن لأي رسالة بريد إلكتروني أن تحصل على احتمالية أعلى من $ 0.0 $. - (0, 1): كلاهما النوعية والحساسية $ 1 = $، يعني عدم وجود توقعات إيجابية ونتائج سلبية False Positive أو توقعات سلبية ونتائج إيجابية False Negative. نموذج ذو منحنى ROC يساوي (0, 1) لدية قيمة مثالية لحد فصل $ C $ للنموذج.
- (1, 0): كلاهما النوعية والحساسية $ 0 = $، يعني عدم وجود توقعات إيجابية ونتائج إيجابية True Positive أو توقعات سلبية ونتائج سلبية True Negative. نموذج ذو منحنى ROC يساوي (1, 0) لدية قيمة لحد فصل $ C $ يتوقع دائمًا نتائج خاطئة لجميع البيانات.
النموذج الذي يتوقع التصنيف بشكل عشوائي يكون فيه المنحنى ROC خط مستقيم مائل تكون فيه النقاط فيها الحساسية ومعدل القيم السلبية التي تم توقعها إيجابياً False Positive متساوية:
plt.step(np.arange(0, 1, 0.001), np.arange(0, 1, 0.001), color='b', alpha=0.2,
where='post')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('Sensitivity')
plt.title('Random Classifier ROC Curve')
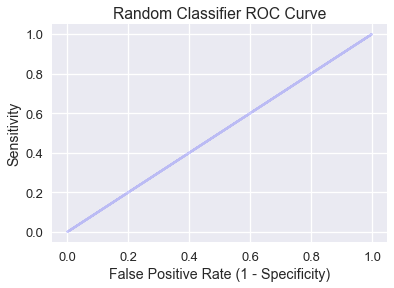
النموذج العشوائي الذي يتوقع الاحتمالية $ p $ لقيمة مُدخلة $ x $ سيتوقع توقعات إيجابية ونتائج إيجابية True Positive أو توقعات إيجابية ونتائج سلبية False Positive لـ $ p $، لذا الحساسية و ومعدل التوقعات الإيجابية والنتائج السلبية False Positive متساويان.
نريد أن يكون منحنى ROC في النموذج أعلى من خط النموذج العشوائي، ونصل الآن لمفهوم AUC.
AUC
المساحة أسفل المنحنى Area Under Curve (AUC) هي المساحة أسفل منحنى ROC وتعمل كأداة لتلخيص أداء النموذج. المساحة أسفل المنحنى للنموذج words_list_model تم رسمها في الأسفل ويمكن حسابها باستخدام دالة AUC في مكتبة scikit-learn: 📝
plt.fill_between(false_positive_rate_values, sensitivity_values, step='post', alpha=0.2,
color='b')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('Sensitivity')
plt.title('words_list_model ROC Curve')
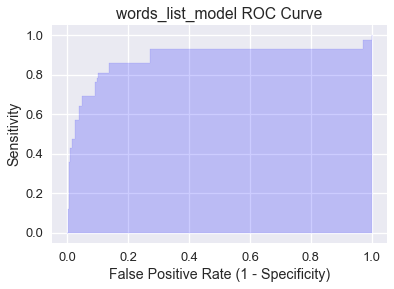
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train, words_list_model_probabilities)
0.9057984671441136
يمكن تفسير AUC على أنها احتمالية أن يقوم النموذج بتعيين قيمة عالية للاحتمالية لنقطة مختارة بشكل عشوائي تنتمي للتصنيف الإيجابي من نقطة مختارة بشكل عشوائي تنتمي للتصنيف السلبي. القيمة المثالية لـ AUC هي 1 يكون فيها النموذج مثالي (منحنى ROC سيكون (0, 1)). حصول النموذج words_list_model على مساحة أسفل المنحنى AUC تساوي 0.906 يعني أن النموذج من المحتمل أن يتوقع الرسائل المزعجة كمزعجة بنسبة 90.6% أكثر من توقعه الرسائل السليمة كمزعجة.
عند التحقق من ذلك، المساحة أسفل المنحنى AUC للنموذج العشوائي تساوي 0.5، على الرغم أن ذلك أيضاً قابل للتغير بشكل قليل بناءًا على العشوائية. النموذج الفعال والمفيد تكون فيه AUC أعلى بكثير من 0.5، والتي حققها النموذج words_list_model. إذا كانت المساحة أسفل المنحنى أقل من 0.5، فإن النموذج أداءه أسوأ من أداء التوقعات العشوائية.
ملخص تقييم النموذج اللوجستي
المساحة أسفل المنحنى AUC هي أداة لتقيم النماذج في البيانات ذات التصنيف الغير متوازن. بعد تدريب النموذج، من الممارسات الممتازة هي إيجاد منحنى ROC وحساب AUC لتحديد الخطوة التالية. إذا كان AUC عالي، نستخدم منحنى ROC لتحديد أفضل قيمة لحد الفصل. ولكن، إذا كانت قيمة AUC غير مرضية، فمن الأفضل القيام بالمزيد من التحليل الاستكشافي للبيانات و إختيار قيم أفضل للخصائص للتحسين من أداء النموذج.
التصنيف متعدد التصنيفات
حتى الآن يقوم النموذج بتصنيف ثنائي فيها النتائج واحد من نتيجتين؛ مثلاً، صنفنا الرسائل كمزعجة أو غير مزعجة. ولكن، الكثير من مشاكل في علم البيانات تحتوي على تصنيفات مُتعددة التصنيفات Multiclass Classification، فيه نريد أن نصنف نتائج البريد الإلكتروني إلى واحد من عدة تصنيفات. مثلاً، تحديد رسائل البريد ما إذا كانت عائلية، من الأصدقاء، خاص بالعمل أو الإعلانات والعروض. لحل هذا النوع من المشاكل، نستخدم طريقة جديدة يطلق عليها تصنيف واحد-ضد-البقية One-vs-Rest (OvR) classification. 📝
تصنيف واحد-ضد-البقية
في هذا النوع من التصنيف (يطلق عليه أيضاً واحد-ضد-الجميع One-vs-All أو OvA)، نقوم بتقسيم مشكلة التصنيف المتعدد التصنيفات إلى مشكلة من عدة تصنيفات ثنائية النتائج. مثلاً، يمكن أن تظهر لنا نتائج بيانات التدريب كالتالي:
shapes = pd.DataFrame(
[[1.3, 3.6, 'triangle'], [1.6, 3.2, 'triangle'], [1.8, 3.8, 'triangle'],
[2.0, 1.2, 'square'], [2.2, 1.9, 'square'], [2.6, 1.4, 'square'],
[3.2, 2.9, 'circle'], [3.5, 2.2, 'circle'], [3.9, 2.5, 'circle']],
columns=['$x_1$', '$x_2$', '$y$']
)
sns.lmplot('$x_1$', '$x_2$', data=shapes, hue='$y$', markers=['^', 's', 'o'], fit_reg=False)
plt.xlim(1.0, 4.0)
plt.ylim(1.0, 4.0);
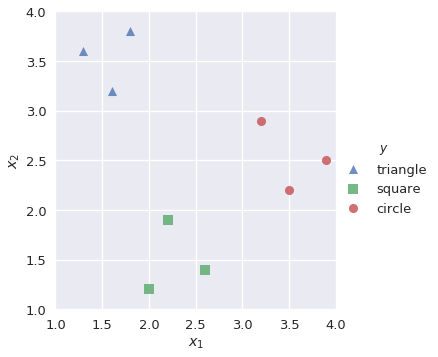
هدفنا هو رسم نموذج متعدد التصنيف يقوم بتوقع النتائج من ثلاث triange، square أو circle عند تمرير القيم $x_1$ و $x_2$ إليه. أولاً نقوم ببناء نموذج ثنائي بأسم lr_triangle يقوم بتوقع النتائج ما إذا كانت مُثلثات triangle أم لا:
plot_binary(shapes, 'triangle')
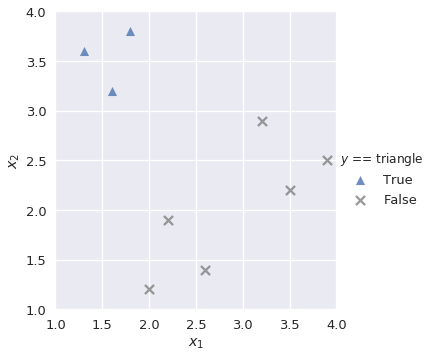
إستعان الكاتب بدالة عرفها بأسم
plot_binaryلمساعدته على إظهار النتائج في رسم بياني، وعرفها كالتالي:markers = {'triangle':['^', sns.color_palette()[0]], 'square':['s', sns.color_palette()[1]], 'circle':['o', sns.color_palette()[2]]} def plot_binary(data, label): data_copy = data.copy() data_copy['$y$ == ' + label] = (data_copy['$y$'] == label).astype('category') sns.lmplot('$x_1$', '$x_2$', data=data_copy, hue='$y$ == ' + label, hue_order=[True, False], markers=[markers[label][0], 'x'], palette=[markers[label][1], 'gray'], fit_reg=False) plt.xlim(1.0, 4.0) plt.ylim(1.0, 4.0);
بنفس الطريقة، نقوم ببناء نموذج lr_square و lr_circle للتصنيفات الأخرى:
plot_binary(shapes, 'square')
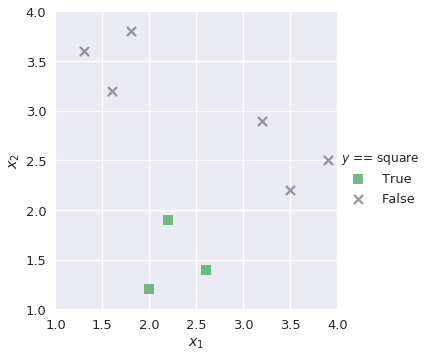
plot_binary(shapes, 'circle')
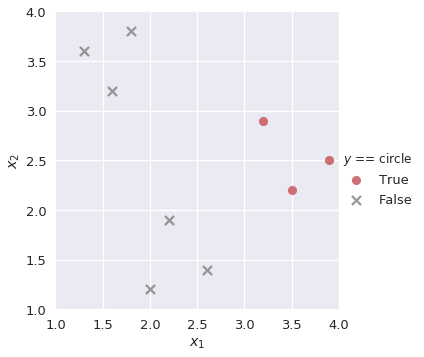
نعلم أن النتائج من الدالة السينية في الانحدار اللوجستي هي عبارة عن احتمالية قيمة بين 0 و 1. لحل التصنيف متعدد التصنيفات لدينا، نبحث عن احتمالية الجانب الإيجابي في كل نموذج ونختار التصنيف الأعلى إيجابية. مثلاً، لو إذا إطلعنا على القيم التالية:
| $x_2$ | $x_1$ |
|---|---|
| 2.5 | 3.2 |
سيقوم النموذج بإدخال هذه القيم إلى كل النماذج السابقة lr_triangle، lr_square، و lr_circle. نقوم بإيجاد القيمة الاحتمالية الإيجابية لكل من النماذج الثلاثة:
from sklearn.linear_model import LogisticRegression
lr_triangle = LogisticRegression(random_state=42)
lr_triangle.fit(shapes[['$x_1$', '$x_2$']], shapes['$y$'] == 'triangle')
proba_triangle = lr_triangle.predict_proba([[3.2, 2.5]])[0][1]
lr_square = LogisticRegression(random_state=42)
lr_square.fit(shapes[['$x_1$', '$x_2$']], shapes['$y$'] == 'square')
proba_square = lr_square.predict_proba([[3.2, 2.5]])[0][1]
lr_circle = LogisticRegression(random_state=42)
lr_circle.fit(shapes[['$x_1$', '$x_2$']], shapes['$y$'] == 'circle')
proba_circle = lr_circle.predict_proba([[3.2, 2.5]])[0][1]
lr_circle |
lr_square |
lr_triangle |
|---|---|---|
| 0.497612 | 0.285079 | 0.145748 |
بما أن الاحتمالية الإيجابية الأعلى هي لدى lr_circle، فإن النموذج متعدد التصنيفات سيتوقع أن القيمة التي اطلع عليها تنتمي إلى التصنيف circle.
تطبيق عملي: بيانات Iris
تعتبر بيانات Iris إحدى أشهر البيانات المستخدمة في علم البيانات لتعلم مفاهيم تعلم الآلة. هناك ثلاث تصنيفات، كل واحدة تمثل أحد أنواع أزهار السوسن Iris:
- Iris-setosa
- Iris-versicolor
- Iris-virginica
هناك أربع خصائص متوفرة في البيانات:
- Sepal length (cm) طول كأس الزهرة (بالسنتيمتر).
- Sepal width (cm) عرض كأس الزهرة (بالسنتيمتر).
- Petal length (cm) طول بتلة الزهرة (بالسنتيمتر).
- Petal width (cm) عرض بتلة الزهرة (سنتيمتر).
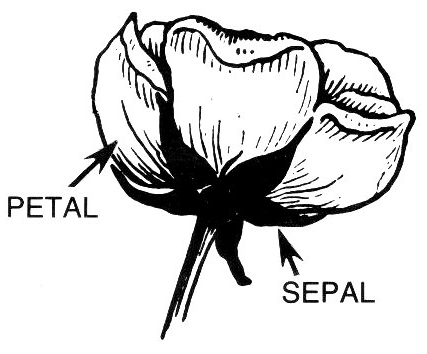
سنقوم بإنشاء نموذج متعدد التصنيفات يقوم بتوقع نوع الزهرة بناءًا على الخصائص الأربعة. أولاً، نقوم بقراءة البيانات:
iris = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
header=None, names=['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species'])
iris
| species | petal_width | petal_length | sepal_width | sepal_length | |
|---|---|---|---|---|---|
| Iris-setosa | 0.2 | 1.4 | 3.5 | 5.1 | 0 |
| Iris-setosa | 0.2 | 1.4 | 3 | 4.9 | 1 |
| Iris-setosa | 0.2 | 1.3 | 3.2 | 4.7 | 2 |
| … | … | … | … | … | … |
| Iris-virginica | 2 | 5.2 | 3 | 6.5 | 147 |
| Iris-virginica | 2.3 | 5.4 | 3.4 | 6.2 | 148 |
| Iris-virginica | 1.8 | 5.1 | 3 | 5.9 | 149 |
150 rows × 5 columns
X, y = iris.drop('species', axis=1), iris['species']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.35, random_state=42)
بعد تقسيم البيانات إلى بيانات تدريب و اختبار، نقوم بضبط النموذج متعدد التصنيفات على بيانات التدريب. بشكل تلقائي، يقوم نموذج الانحدار اللوجستي LogisticRegression في مكتبة scikit-learn بتحديد قيمة المتغير multi_class='ovr'، والتي تقوم بإنشاء نموذج ثنائي لكل تصنيف مختلف:
lr = LogisticRegression(random_state=42)
lr.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=42, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
نقوم بالتوقع باستخدام بيانات الاختبار، ثم نستخدم مصفوفة الدقة لتقييم النتائج:
y_pred = lr.predict(X_test)
plot_confusion_matrix(y_test, y_pred)
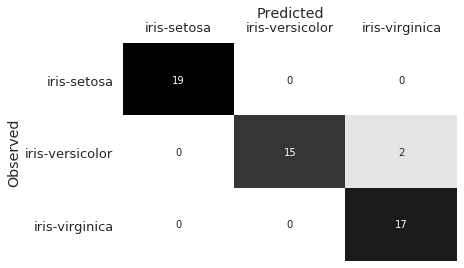
إستخدم الكاتب الدالة
plot_confusion_matrixوالتي عرفها لمساعدته لعرض وتقييم النتائج على شكل مصفوفة الدقة:def plot_confusion_matrix(y_test, y_pred): sns.heatmap(confusion_matrix(y_test, y_pred), annot=True, cbar=False, cmap=matplotlib.cm.get_cmap('gist_yarg')) plt.ylabel('Observed') plt.xlabel('Predicted') plt.xticks([0.5, 1.5, 2.5], ['iris-setosa', 'iris-versicolor', 'iris-virginica']) plt.yticks([0.5, 1.5, 2.5], ['iris-setosa', 'iris-versicolor', 'iris-virginica'], rotation='horizontal') ax = plt.gca() ax.xaxis.set_ticks_position('top') ax.xaxis.set_label_position('top')
يظهر من مصفوفة الدقة السابقة أن النموذج أخطأ في التوقع مرتين للتصنيف Iris-versicolor وتوقعها كتصنيف Iris-virginica. عند التحقق من الخصائص sepal_length و sepal_width، نستطيع أن نرى سبب حدوث ذلك:
sns.lmplot(x='sepal_length', y='sepal_width', data=iris, hue='species', fit_reg=False);
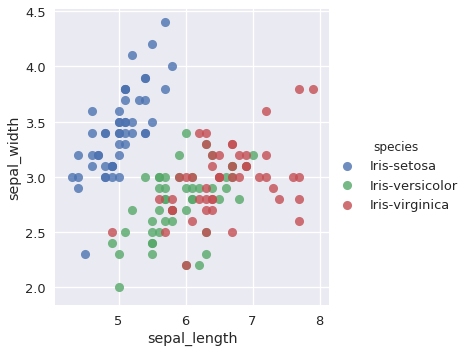
تتداخل الكثير من النقاط في للتصنيفات Iris-versicolor و Iris-virginica. على الرغم أن الخصائص الأخرى (petal_width و petal_length) تقدم معلومات أكثر للتفريق بين التصنيفان، إلا أن النموذج أخطأ في تصنيف نوعين من الزهور.
كما في العالم الحقيقي، تحدث التصنيفات الخطأ عندما يكون تصنيفان متشابهان في الخصائص. مصفوفات الدقة مفيدة كونها تطلعنا على الأخطاء التي يقع فيها النموذج، أيضاً تقدم لنا أفكار عن أي نوع من الخصائص نحتاج أن نوجدها من أجل تحسين أداء النموذج.
التصنيف متعدد النتائج
نوع آخر من مشاكل التصنيف هو التصنيف متعدد النتائج Multilabel Classification، وفيه يكون للنتيجة أكثر من تصنيف. مثال لذلك في نظام لتصنيف الملفات: الملف قد يكون ذو إيجابي أو سلبي، ذو محتوى ديني أو غير ديني، و متفتح أو محافظ. مشكلة متعددة النتائج قد تكون أيضاً متعددة التصنيفات؛ قد نرغب أن يكون نظام التصنيف للملفات لدينا يفرق بين قائمة من الأنواع، أو يحدد اللغة التي كُتب فيها الملف. 📝
يمكن أن نطبق التصنيف متعدد النتائج ببساطة عبر تدريب نماذج منفصلة لكل نوع من النتائج. لتصنيف نقطة ما، نقوم بجمع جميع نتائج توقعات النماذج.
ملخص التصنيف متعدد الاحتمالات
مشاكل التصنيف قد تكون صعبة. في بعض الأحيان، نحتاج في المشكلة للتفريق بين أكثر من تصنيف؛ وفي بعض الأحيان قد نريد تعين أكثر من نتيجة لكل قيمة يطلع علينا النموذج. نستعين بما نعرفه عن النماذج ثنائية النتائج لبناء أنظمة تصنيف متعدد التصنيفات والنتائج والتي قادرة على أداء تلك المهام.