مبادئ وتقنيات علم البيانات

الفصل الثاني: تصميم البيانات

فهرس الفصل:

• مقدمة

• ديوي يهزم ترومان
• 1936: كارثة الاستطلاع السابق
• 1948: تصويت غالوب
• المشكله في العينه الحصصيه
• البيانات الضخمة؟

• نظرة عامة على الاحتمالات
• احتمالية الأحداث
• A أو B
• A و B

• استخدام الاحتمالات لإيجاد العينات
• العينة العشوائية البسيطة
• العينة العنقودية Cluster Sampling
• العينة الطبقية Stratified Sampling
• لماذا عينة الاحتمالات؟

• العينة العشوائية البسيطة × البيانات الضخمة

مقدمة

البيانات هي عصب علم البيانات. لذا من الصعب البدء بتحليل البيانات دون معرفة كيف تم جمعها.

في هذا الفصل سنتحدث عن تصميم البيانات، خطوة جمع وتكوين البيانات. الكثير من علماء البيانات استنتجوا نتائج مبكرة غير صحيحه لأنهم لم يتمكنوا من فهم بياناتهم. سنقوم باستعراض أمثله لتأكيد أهمية هذه النقطة، وأهمية استخدام الاحتمالات في علم البيانات لإيجاد العينات .

ديوي يهزم ترومان

في صراع الرئاسة الأمريكية عام 1948، كان عمدة نيويورك “توماس ديوي” منافساً لـ “هاري ترومان”. كالعادة، أجرت عدة وكالات مختصه بالاستطلاع والتصويت بعض الاستطلاعات للتنبؤ بالفائز في السباق الرئاسي.

1936: كارثة الاستطلاع السابق

في عام 1936، أي ثلاث سباقات انتخابية قبل 1948، توقعت مجلة The Literary Digest خسارة “فرانكلين روزفلت” وفوز ساحق لمنافسه “آلف لاندن”. وكان تبرير المجلة أنها قامت بأخذ عينه تصويت لأكثر من مليونين شخص اعتماداً على أرقام الهواتف ومعلومات السيارات المسجلة. وكما يبدو واضحاً، هذه العينة تحتوي على تحيز كبير، لأن في تلك الفترة كان أغلب مالكي الهواتف والسيارات أغنى ممّن لا يملكونها. في هذه الحالة، التحيز كان كبيراً حيث جعل المجلة تتوقع أن “روزفلت” سيحصل على 43% من إجمالي الأصوات، ولكنه في النهاية حصل على 61%، بفارق حوالي 20% عن توقع المجلة ويعتبر من أكبر الأخطاء التي حدثت في استطلاع عام. بعد ذلك بفتره قصيرة، أغلقت المجلة ولم تعد تعمل. 📝

1948: تصويت غالوب

رغبة في التعلم من الأخطاء السابقة، قامت “مؤسسة غالوب” باستخدام طريقة سميت ب “عينة الحصة Quota Sampling” لتوقع نتيجة انتخابات الرئاسة الأمريكية لعام 1948. في فترة جمع العينات، كل مُحاوِر استطلع رأي مجموعة أشخاص من كل فئة ديموغرافية. مثلاً، كل محاور يجب أن يستطلع رأي الذكور والإناث، بمختلف الأعمار، الأعراق، ومستوى الدخل، ليطابق التراكيب السكانية في تعدادت الولايات المتحدة. تم ذلك للتأكد أن التصويت لن يترك أي فئة من مجموع المصوتين.

باستخدام هذه الطريقة، توقعت “غالوب” أن “توماس ديوي” سيكسب أصواتاً أكثر من “هاري ترومان” بنسبة 5%. الفارق كان ملحوظاً ليجعل صحيفة Chicago Tribune تطبع العنوان بشكل عريض “ديوي يهزم ترومان”:

كما نعرف الآن، “ترومان” هو من انتصر بسباق الرئاسة. بالأصح، فاز بفارق 5% عن “ديوي”! ما الخطأ الذي حدث في تصويت “مؤسسة غالوب”؟ 📝

المشكلة في العينة الحصصية

رغم أن الطريقة تساعد منظمي الاستطلاعات على تقليل الانحياز في جمع البيانات، لكنها أظهرت انحيازاً من جهة أخرى. حيث أخبرت المؤسسة محاوريها أن بإمكانهم مقابلة أياً كان طالما أنهم ينجزون الحصة المخصصة لهم. هذه إحدى التفسيرات عن سبب حصول المحاورين على عدد غير متناسب من الجمهوريين. في ذلك الوقت، يعتبر الجمهوريون متوسطي الثراء وغالباً ما يعيشون في أحياء راقية، مما يجعلهم أسهل لإجراء المقابلة. يدعم هذا التفسير حقيقة أن المؤسسة توقعت نسبة 2-6% أكثر لأصوات الجمهوريين مقارنة بالأرقام الحقيقية للانتخابات الثلاث السابقة.

هذه الأمثلة تظهر أهمية فهم الانحياز أثناء خطوة جمع البيانات. Literary Digest و “مؤسسة غالوب” كلاهما قامتا بنفس الخطأ، اعتقاداً أن طريقتهم غير منحازة بينما في الحقيقة كلا الطريقتين كانتا تعتمدان على أحكام المحاورين.

نحن الآن نعتمد على العينات المحتملة، إحدى طرق جمع العينات والتي تخصص احتمالات معينة لظهور أي عينة، للتقليل من الانحياز في جمع بياناتنا.

البيانات الضخمة؟

في عصر البيانات الضخمة، نحاول التقليل من الانحياز بجمع المزيد من البيانات. في النهاية، نحن نعلم أنها ستعطينا احتمالات مناسبة؛ أليست كل العينات الكبيرة تعطينا احتمالات مناسبة أياً كانت طريقة جمع العينة؟

سنعود لهذا السؤال بعد مناقشة طرق جمع العينات المحتملة لمقارنة كلا الطريقتين.

نظرة عامة على الاحتمالات

الكثير من المبادئ الأساسية في علم البيانات، يشمل ذلك تصميم البيانات، تعتمد على قوانين معينة. قانون الاحتمالات Probability يسمح لنا بتحديد احتمالية حدوث شيء ما. في هذا الفصل سنستعرض مراجعة سريعة عن الاحتمالات وأهميتها.

لنفرض أن لدينا عملتين معدنيتين، بجهة توجد صورة $ H $ (Head) وفي الجهة الأخرى كتابة $ T $ (Tails). إذا أردنا رمي العملتين ومشاهدة النتيجة نسمي ذلك بالتجربة Experiment. و فضاء النتائج Outcome Space $ \Omega $ يشمل جميع النتائج المحتملة لهذه التجربة. فضاء نتائج تجربتنا هو: $ \Omega = \{ HH, HT, TH, TT \} $.

الحدث Event هي أحد النتائج من فضاء النتائج. على سبيل المثال، الحصول على $ H $ واحد و $ T $ واحد هو أحد الأحداث من تجربتنا. هذا الحدث يتكون في النتائج $\{HT, TH\}$. نستخدم الرمز $ P(\text{event})$ للتعبير عن احتمالية الحدث، في مثالنا نرمز لها ب: $ P(\text{One Head and One tails})$ (احتمالية ظهور صورة مرة وكتابة مرة).

احتمالية الأحداث

في هذا الكتاب، سنتعامل مع مشاكل لديها فضاءات نتائج تكون فيها احتمالية حدوث أي من النتائج متساوي. هذه الفضاءات لديها معادلة حسابية بسيطة لحساب الاحتمالية. المعادلة هي: عدد النتائج المحتملة للحدث قسمة عدد جميع الأحداث في فضاء النتائج:

نسبة احتمالية الحدث = $ P(\text event) = \frac {\text {# of outcomes in event}}{\text {# of all possible outcomes}} $

في مثال رمي العملتين المعدنيتين، احتمالية حدوث جميع الأحداث $\{ HH, HT, TH, TT \}$ متساوية. لحساب $ P(\text{One Head and One tails})$، نجد أن احتمال حدوث الحدث هي 2 من مجموع الأحداث 4:

يوجد لدينا ثلاث أساسيات مسلّم بها في حساب الاحتمالات:

• احتمالية حدوث أي حدث هي عدد حقيقي بين 0 و 1: $ 0\le P(\text {event}) \le 1 $.
• مجموع احتمالية جميع الأحداث في فضاء العينة هو 1: $ P( \Omega ) = 1 $.
• الثالثة تتضمن الأحداث التي لا تحدث مع بعضها Mutually Exclusive مثل:
  • A أو B ( $ A \cup B $ ).
  • A و B ( $ A \cap B $ ).
  • B بشرط حدوث A أولاً ( $ B|A $).

A أو B

عادةً ما نحاول إيجاد احتمالية حدوث $ A $ أو $ B $. مثلاً، مؤسسة متخصصة في الاقتراع والتصويت تريد إيجاد احتمالية اختيار شخص بشكل عشوائي بحيث يكون عمره 17 أو 18 سنه. ذكرنا أن الأحداث لا يمكن حدوثها في نفس الوقت Mutually Exclusive. إذا كانت $ A $ هي اختيارنا لشخص بعمر 17 سنة، و $ B $ هي اختيارنا لشخص بعمر 18 سنة، فإن حدوث $ A $ و $ B $ معاً مستحيل لأنه لا يمكن للشخص أن يكون عمره 17 و 18 في نفس الوقت.

لحساب احتمالية $ P(A \cup B)$:

التعداد السكاني لعام 2010 في الولايات المتحدة أظهر أن 1.4% من السكان الأمريكيين بعمر 17 سنة، و 1.5% بعمر 18 سنة. لذا إذا اخترنا شخصاً بشكل عشوائي من السكان فإن احتمالية أن عمره 17 سنة هي $ P(A) = 0.014 $ و احتمالية أن عمره 18 سنة هي $ P(B) = 0.015 $، ذلك يعني احتمالية اختيارنا لشخص بشكل عشوائي عمره 17 أو 18 سنه هي:

لتوضيح الفكرة بشكل أكثر لنقم بشرحها على رسم Venn البياني:

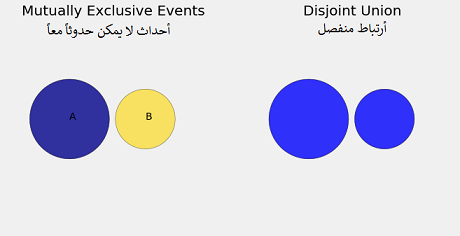
عندما يكون الحدثان $ A $ و $ B $ الذين لا يمكن حدوثهما معاً، فلا توجد نتائج تظهر في $ A $ و $ B $ معاً. لذا إذا كانت $ A $ تحتوي على 5 نتائج و $ B $ تحتوي على 4. فإن $ A \cup B $ لديها 9 نتائج مُحتملة.

عندما تكون إمكانية ظهور النتائج معاً ممكنة فإنه لا يمكن تطبيق عملية الجمع عليها. لنعود لمثال العملتين المعدنيتين، نجد عند رمي العملة المعدنية أن نتيجة مؤكدة واحدة هي صورة أو نتيجة مؤكدة واحدة هي كتابة.

إذا كانت $ A $ هي حدث ظهور صورة مرة واحدة، إذاً الاحتمالية هي $ P(A) = \frac {2}{4}$ لأن فضاء $ A $ يحتوي على النتائج $\{ HT, TH \}$ و مجموع النتائج المحتملة هو 4. وإذا كانت $ B $ هي حدث ظهور كتابة مرة واحدة، إذاً احتماله يساوي $ P(B) = \frac {2}{4} $ لأن فضاء نتائج $ B $ أيضاً يحتوي على $\{ HT, TH \}$. ولكن الحدث $ A \cup B $ يحتوي على نتيجتين فقط لأن النتيجتين هنا متشابهتان في $ A $ و $ B $ وهي $ P(A \cup B) = \frac {1}{2}$. القيام هنا بجمع النتائج لاحتساب الاحتمالات يوصلنا لنتيجة خاطئة. هناك نتائج تظهر في $ A $ و $ B $; إضافة الرقمين لنتائج $ A $ و $ B $ في هذا المثال فسنكون قد حسبناهما مرتين. في الرسم البياني التالي يظهر الجزء المشترك بين $ A $ و $ B $.

لحل هذه المشكلة، نحتاج لطرح احتمالية $ P(A \cap B) $. ولحسابها نقوم بالتالي:

لاحظ أنه عندما تكون احتمالية ظهور الأحداث $ A $ و $ B $ معاً مستحيلة، فإن $ P(A \cap B) = 0 $ وبالتالي تظهر المعادلة السابقة.

A و B

نحاول أحياناً إيجاد احتمالية حدوث كلا الحدثين $ A $ و $ B $ معاً. على سبيل المثال، إذا كان لدينا فصل بثلاث طلاب $ X $، $ Y $ و $ Z $. ما هي احتمالية أن نختار عينة واحدة بحجم 2 يكون فيها $ Y $ القيمة الأولى وتليها $ X $؟و دون أن نعيد عملية سحب العينة؟

إحدى الطرق لإيجاد الاحتمالية هي سرد جميع الاحتمالات الممكن حدوثها:

بما أننا نرغب بسحب عينه واحدة يكون فيها $ Y $ أولاً ويتبعها $ X $ فإن النتيجة هي:

يمكن تقسيم الاحتمالية إلى قسمين، الأولى هي سحب العنصر $ Y $ أولاً، والثانية هي سحب $ X $ بعد $ Y $. إذاً احتمالية سحب $ Y $ أولاً هي $\frac {1}{3}$ لأن هناك ثلاث احتمالات ممكن أن تُسحب وهي $ X $،$ Y $ و $ Z $.

بعد سحب $ Y $، فضاء النتائج لعملية السحب الثانية تحتوي على $\{X,Z\}$، ويعني ذلك أن احتمالية سحب $ X $ كعنصر ثاني هي $\frac {1}{2}$. تسمى هذي الاحتمالية ب الاحتمال الشرطي Conditional Probability، وهي احتمالية سحب $ X $ بعد أن سحبنا $ Y $ أولاً. نستخدم الرمز $ P(B | A)$ للاحتمالية المشروطة ونعني هنا أن احتمالية حدوث $ B $ بشرط حدوث $ A $ مُسبقاً.

لنستعرض التالي:

قاعدة الضرب السابقة هي إحدى قواعد الاحتمالات العامة، لأي حدث $ A $ و $ B $، احتمالية حدوث كليهما هي:

في بعض الحالات، كلا الحدثين مستقلين Independent Events عن بعضهما. احتمالية ظهور $ B $ ثانياً لا يتأثر إذا ظهر $ A $ أولاً أو لم تظهر. مثلاً، في حجر النرد، ظهور الرقم 6 لا يؤثر شيئاً على احتمالية ظهور الرقم 5 بعده. إذا كانت $ A $ و $ B $ مستقلين فإن: $ P(B|A) = P(B) $. هذه تُبسط لنا قاعدة الضرب:

رغم أن ذلك يسهل لنا عملية الحساب، إلا أن في الواقع وعند مواجهة بيانات حقيقية، الأحداث ليست مستقلة عن بعضها، حتى ولو بدت العلاقة بينهما غير واضحة في البداية. مثلاً، احتمالية الاختيار العشوائي لمواطن أمريكي عمره 90 سنة أو أعلى ليست مستقلة عن كون المواطن ذكر أو أنثى، لأننا أعطينا أن الشخص عمرة 90 سنة، فإن احتمالية أن يكون الشخص أنثى أكثر مرتين من أن يكون ذكراً.

كعلماء بيانات، يجب علينا التحقق من الفرضيات واستقلاليتها بشكل دقيق! سقوط سوق عقار المنازل الأمريكية عام 2008 كان يُمكن تفاديه لو لم تفترض البنوك أن أسعار المنازل تختلف من مدينة لأخرى بشكل مستقل. (المزيد عن ذلك هنا)

للمزيد عن الاحتمالات: 📝 📝

استخدام الاحتمالات لإيجاد العينات

على عكس الطريقة العادية لإيجاد العينات أو السحب العشوائي، استخدام الاحتمالات لإيجاد العينات يمكننا من تحديد بعض الصفات التي يجب توفرها في العينة. توجد طريقتان لإيجاد العينات باستخدام الاحتمالات: العينة العنقودية Cluster Sampling و العينة الطبقية Stratified Sampling.

إذا كان لدينا 6 أشخاص. وأعطينا كل شخص حرفاً مختلفاً من $ A $ إلى $ F $:

العينة العشوائية البسيطة

للحصول على عينة عشوائية ذات حجم 2 من مجموعة الأشخاص، يمكننا كتابة حرف كل شخص على ورقة، وضعها في صندوق، خلطها، ثم سحب ورقتين. ببساطة هذه هي طريقة العينة العشوائية البسيطة.

النتائج المحتملة ذات الحجم 2 هي:

يوجد لدينا 15 عينة محتمل حدوثها ذات الحجم 2 من مجموع الأشخاص الستة. طريقة أخرى لحساب مجموع العينات المحتملة: 📝

بما أن السحب يتم بطريقة عشوائية وجميع العينات متساوية باحتمالات سحبها، فإن احتمالية سحب كل عينة من الـ15 نتائج المحتملة هي:

يمكننا أيضاً توقع احتمالية ظهور عنصر معين في العينة بحجم 2. مثلاً، العنصر $ A $ يظهر 5 مرات في القوائم التي عرضناها سابقاً، إذاً:

ينطبق هذا المثال على جميع العناصر الأخرى:

توجد طريقة أخرى لحساب احتمالية ظهور عنصر معين. مثلاً لظهور $ A $ في العينة، يجب علينا سحبها أولاً أو ثانياً. إذاً:

العينة العنقودية Cluster Sampling

في العينة العنقودية نقوم بتقسيم البيانات إلى مجموعات. ثم نستخدم مفاهيم العينة العشوائية البسيطة لاختيار المجموعات بشكل عشوائي.

مثلاً، إذا كان لدينا 6 أشخاص ثم جمعناهم في مجموعات من شخصين: $(A,B) ~ (C,D) ~ (E,F)$ ليتم تكوين 3 عناقيد (مجموعات) من شخصين. نستخدم الآن العينة العشوائية البسيطة على هذه العناقيد. كما فعلنا سابقاً، لإيجاد احتمالية ظهور $ A $ في العينة:

وبنفس النتيجة، فإن احتمالية ظهور أي شخص في العينة العشوائية هو $\frac{1}{3}$. نلاحظ أن الاختلاف الوحيد بين هذه الطريقة وطريقة العينة العشوائية البسيطة هو في العينات نفسها. مثلاً، في العينة العشوائية البسيطة احتمالية حصولنا على $ AB $ هو نفس احتمالية حصولنا على $ AC $ وهي $\frac{1}{15}$. ولكن في العينة العنقودية الاحتمالية هي:

لأن $ A $ و $ C $ لا يظهران معاً في نفس المجموعة.

إذاً لماذا نستخدم العينة العنقودية؟ الطريقة فعالة جداً لأنها تسهل تجميع العينات. مثلاً، يعتبر من الأسهل إجراء استطلاع في مدينة مكونة من 100 شخص بدلاً من استطلاع آلاف الأشخاص موزعين على عدد مختلف من المدن والولايات. لهذا الكثير من مؤسسات التصويت هذه الأيام تستخدم العينات العنقودية لإجراء استطلاعاتها.

السلبية الوحيدة في العينة العنقودية هي أنها قد تظهر اختلاف Variance كبير في التوقع. يعني ذلك أننا نحتاج لأخذ عينات أكبر عند استخدام هذه الطريقة. ولاحظ أن في الواقع هذا أعقد بكثير من مثالنا السابق. 📝 📝

العينة الطبقية Stratified Sampling

كما يظهر من اسمها، في العينة الطبقية نقسم البيانات إلى طبقات، ثم نوجد عينة عشوائية بسيطة لكل طبقة. في كلا النوعين، الطبقية والعنقودية، نقسم البيانات إلى مجموعات، في العنقودية نستخدم العينة العشوائية البسيطة مرة واحدة، وفي العينة الطبقية نستخدمها أكثر من مرة (في كل مجموعة).

على نفس المثال السابق، يمكننا تقسيم الأشخاص الستة إلى الطبقتين التاليتين:

نستخدم العينة العشوائية البسيطة على كُل طبقة لنستخرج قيمة واحدة لنكون المجموعة المطلوبة والتي حجمها يساوي 2. الاحتمالات التي يمكن أن تحدث هي:

مرة أخرى، يمكننا إيجاد احتمالية وجود $ A $ في عينتنا العشوائية:

كما في العينة العنقودية، احتمالية $ P(AB)= 0 $ لأن $ A $ و $ B $ في نفس الطبقة.

كلا الطريقتين، العنقودية والطبقية، ينتجان نتائج مختلفة للاحتمالات بناءً على طريقة تقسيم البيانات فيهما. ويمكن ملاحظة أنه لا يجب أن تكون كل التقسيمات (الطبقات) متساوية الحجم. على سبيل المثال، يمكننا تقسيم الولايات المتحدة بناءً على الوظائف، ثم نأخذ عينات من كل طبقة بناءً على نسبة توزيع الوظائف، إذا كان فقط 0.01% منهم إحصائيين، فيجب أن نتأكد أن 0.01% من نسبة عينتنا تحتوي على إحصائيين.

إذا كنت تتوقع أن عينة الطبقات هي الأفضل للاستخدام للقيام بالعينة الحصصية Qouta Sampling فأنت على صواب. عينة الطبقات تسمح للباحث بالتأكد أن جميع الطبقات والمجموعات الفرعية ممثلة بشكل مناسب في العينة النهائية دون تدخل بشري لاختيار العينات. هذا قد يقلل أحياناً من الاختلاف في التوقع، ولكن العينة الطبقية قد تكون أصعب لأننا أحياناً لا نعرف حجم كل طبقة. 📝 📝

لماذا عينة الاحتمالات؟

تساعدنا عينة الاحتمالات في تحديد عدم يقيننا في تقدير أو تنبؤ. فقط بهذه الخطوة يمكننا اختبار فرضياتنا واستنتاجاتنا. كُن حذراً من أن يعطيك شخصاً قيمة عينة الاحتمالات أو مستويات الثقة في مشاريعهم دون شرح وافي وواضح عن طريقتهم في إيجاد العينات.

الآن بما أننا فهمنا عينة الاحتمالات، لنقارن بين العينة العشوائية البسيطة والبيانات الضخمة.

العينة العشوائية البسيطة × البيانات الضخمة

كما ذكرنا سابقاً، قد يبدو أسهل لنا استخدام بيانات أكثر للتخلص من الانحياز. صحيح أن جمع بيانات أكثر منطقياً يظهر نتائج غير متحيزة، ربما لن يكون الانحياز مشكلة بالنسبة لنا إذا ما قمنا فقط بجمع المزيد من البيانات.

لنتخيل أننا منظمي استطلاعات ونريد توقع الرئيس القادم للولايات المتحدة الأمريكية في 2012، السباق كان بين “باراك أوباما” و “ميت رومني”. بما أننا نعرف اليوم من فاز في هذا السباق، يمكننا أن نقارن بين توقعات العينة العشوائية البسيطة و توقعات البيانات الغير عشوائية الضخمة، يطلق عليها أحياناً البيانات الإدارية Administrative Datasets لأنها بيانات تُجمع من أنظمة إدارية.

سنقارن بين بيانات عشوائية بسيطه حجمها 400، وبيانات غير عشوائية ضخمة حجمها 60,000,000. بياناتنا الغير عشوائية حجمها أكثر ب150,000 مرة عن بياناتنا العشوائية!

في الرسم البياني التالي مقارنة بين النتائج الحقيقة لسباق الرئاسة والعينة الغير عشوائية. اللون الأزرق Truth تعني الأرقام الحقيقة التي حصل عليها كل مرشح، اللون الأخضر Big يظهر الأرقام من بياناتنا الضخمة:

total = 129085410
obama_true_count = 65915795
romney_true_count = 60933504
obama_true = obama_true_count / total
romney_true = romney_true_count / total

# 1 percent off
obama_big = obama_true - 0.01
romney_big = romney_true + 0.01

pd.DataFrame({
    'truth': [obama_true, romney_true],
    'big': [obama_big, romney_big],
}, index=['Obama', 'Romney'], columns=['truth', 'big']).plot.bar()
plt.title('Truth compared to a big non-random dataset')
plt.xlabel('Candidate')
plt.ylabel('Proportion of popular vote')
plt.ylim(0, 0.75);

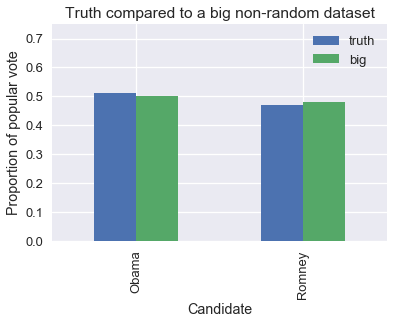
يمكن أن نرى أن البيانات الغير عشوائية الضخمة انحازت قليلاً للمرشح الجمهوري “ميت رومني”، كما كانت في تصويت غالوب عام 1948. لنرى تأثير هذا الانحياز، لنأخذ عينة عشوائية بسيطه من 400 شخص و عينه ضخمة غير عشوائية حجمها 60,000,000. سنحسب نسبة المصوتين للمرشح “باراك أوباما” في كل عينة:

srs_size = 400
big_size = 60000000
replications = 10000

def resample(size, prop, replications):
    return np.random.binomial(n=size, p=prop, size=replications) / size

srs_simulations = resample(srs_size, obama_true, replications)
big_simulations = resample(big_size, obama_big, replications)

ولرسم النتائج، بنفس الألوان السابقة، اللون الأزرق يعني البيانات العشوائية البسيطة، واللون الأخضر يعني نتائج توقع البيانات الضخمة، الخط الأحمر هي النتائج الحقيقية:

bins = bins=np.arange(0.47, 0.55, 0.005)
plt.hist(srs_simulations, bins=bins, alpha=0.7, normed=True, label='srs')
plt.hist(big_simulations, bins=bins, alpha=0.7, normed=True, label='big')

plt.title('Proportion of Obama Voters for SRS and Big Data')
plt.xlabel('Proportion')
plt.ylabel('Percent per unit')
plt.xlim(0.47, 0.55)
plt.ylim(0, 50)
plt.axvline(x=obama_true, color='r', label='truth')
plt.legend();

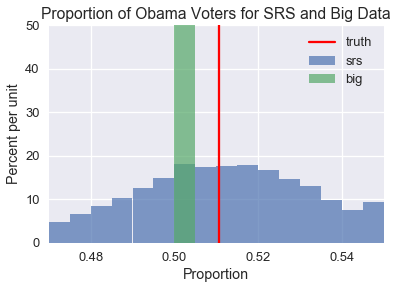
كما نرى، توزيع نتائج البيانات العشوائيه البسيطه مُتركز حول النتيجه الحقيقه للتصويت، بينما توزيع البيانات الغير عشوائيه الضخمه عكس ذلك، ولم ينتج أي تنبؤ صحيح لنسبة المصوتين الحقيقيه. إذا اردنا أن نكون مجالاً للثقه Confidence Intervals باستخدام البيانات الغير عشوائيه، فلن يحتوي أياً منها على نسبه التصويت الحقيقه. لجعل الأمر أكثر سوءًا، مجال الثقة سيكون نحيفاً جداً لأن العينه كبيره. وبالتأكيد ستظهر لنا توقعات خاطئة. 📝 📝

في الحقيقة، عندما تكون طريقة إيجاد العينه لدينا مُنحازه فإن توقعنا عادة ما يكون في البدايه سيء، وكلما جمعنا المزيد من البيانات فأننا نؤكد خطأ نتائجنا. للقيام بتوقعات صحيحه حتى باستخدام عينات متحيزه قليلاً، العينه يجب أن يكون حجمها مقارب لحجم المجموعه، وهذا مطلب لا يمكن تنفيذه عادةً. جودة البيانات تهم أكثر بكثير من حجمها.

ملخص الفصل الثاني

قبل قبول نتائج تحليل البيانات، يجب أن نتحقق من جودة البيانات. يجب أن نسأل أنفسنا الأسئله التاليه:

• هل البيانات كامله (تحتوي على كامل المجموعه التي تهمنا)؟ إذا كانت كذلك، يمكننا إذاً إيجاد خصائص المجموعات دون الحاجة للإستدلال.
• إذا كانت البيانات عينه، كيف تم جمع العينه؟ للقيام بالإستدلال بشكل صحيح، يجب أن تكون البيانات قد جمعت باستخدام طريقه تستخدم الاحتمالات، ويتم شرحها بشكل كامل.
• ما هي التعديلات التي تمت على البيانات قبل إيجاد النتائج؟ هل أثرت هذه التعديلات على جودة البيانات؟

للحصول على معلومات أكثر ومقارنه بين العينات العشوائيه البسيطه والغير عشوائيه الضخمه، نقترح مشاهدة هذا الدرس بواسطة الإحصائي تشاو لي مينق.