مبادئ وتقنيات علم البيانات
الفصل الخامس عشر: المقايضة بين الانحياز والتباين
فهرس الفصل:
مقدمة
في بعض الأحيان، نختار نموذج بسيط جداً ليمثل البيانات. وفي بعض المرات، نختار نموذجاً معقد، بسبب ضبطنا على الضوضاء في البيانات بدلاً من البيانات نفسها.
لفهم سبب قيامنا بذلك، نقوم بتحليل النموذج باستخدام أدوات الاحتمالات والإحصاء. هذه الأدوات تسمح لنا بالتعميم من أمثله بسيطة محدودة حتى وصف المهام الأساسية في النمذجة. بشكل خاص، سنستخدم التوقع Expectation و التباين Variance لعرض وفهم المقايضة بين الانحياز والتباين.
تقليل المخاطر والخسائر
للقيام بالتوقع باستخدام البيانات، نقوم بتعريف نموذج، اختيار دالة خسارة لجميع البيانات، وضبط النموذج مع المتغيرات عن طريق تقليل الخسارة. مثلاً، للقيام بالانحدار الخطي للمربعات الصغرى، نختار النموذج:
\[\begin{aligned} f_\hat{\theta} (x) &= \hat{\theta} \cdot x \end{aligned}\]ودالة الخسارة:
\[\begin{split} \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2\\ \end{aligned} \end{split}\]كما فعلنا مسبقاً، نستخدم $ \hat{\theta} $ كمصفوفة لمتغيرات النموذج، و $ x $ متّجه تحتوي على سطر من مصفوفة البيانات $ X $، و $ y $ هي مصفوفة للبيانات التي تعلم عليها لتساعد على التوقع. $ X_i $ هي السطر $ i $ من المصفوفة $ X $ و $ y_i $ هي النتيجة رقم $ i $ في المصفوفة $ y $.
لاحظ أن الخسارة لكامل البيانات هي متوسط نتائج دالة الخسارة لكل سطر فيها. إذا قمنا بتعريف دالة الخسارة التربيعية:
\[\begin{aligned} \ell(y_i, f_\hat{\theta} (x)) &= (y_i - f_\hat{\theta} (x))^2 \end{aligned}\]إذاً، يمكننا إعادة كتابة متوسط الخسارة بشكل أبسط:
\[\begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i} \ell(y_i, f_\hat{\theta} (X_i)) \end{aligned}\]التعريف في الأعلى يختصر فكرة دالة الخسارة؛ أياً كانت دالة الخسارة التي نستخدمها، خسارتنا لكامل البيانات هي متوسط الخسارة.
بالتقليل من متوسط الخسارة، نختار متغيرات النموذج التي تضبطه بناءًا على البيانات التي يتعلم منها. حتى الآن، لم نقل شيئاً عن المجتمع الإحصائي الذي أنشأ البيانات. في الحقيقة، نحن مهتمين بإجراء توقعات على جميع المجتمع الإحصائي، ليس فقط البيانات التي رأيناها.
المخاطر
إذا كانت البيانات التي رأيناها $ X $ و $ y $ تم جمعها بشكل عشوائي، فأنها تعتبر بياناتنا تعتبر متغيرات عشوائية. وإذا كانت متغيرات عشوائية، فإن متغيرات النموذج أيضاً عشوائية، في كل مرة نجمع فيها المزيد من البيانات ونضبط النموذج عليها، متغيرات النموذج $ f_\hat{\theta} (x) $ ستتغير قليلاً.
لنفترض أننا قمنا بسحب أحد المدخلات والمخرجات $ z, \gamma $ من مجتمعنا الإحصائي بشكل عشوائي. الخسارة التي يكونها النموذج لهذه القيم هي:
\[\begin{aligned} \ell(\gamma, f_\hat{\theta} (z)) \end{aligned}\]لاحظ أن هذه الخسارة هي متغير عشوائي؛ تتغير الخسارة عندما تستقبل قيم جديده من $ X $ و $ y $ ونقاط أخرى من $ z, \gamma $ من المجتمع الإحصائي.
المخاطر Risk لنموذج $ f_\hat{\theta} $ هي النتيجة المتوقعة من الخسارة السابقة لجميع بيانات التدريب $ X $ و $ y $ وجميع النقاط $ z, \gamma $ في المجتمع الإحصائي:
\[\begin{aligned} R(f_\hat{\theta}(x)) = \mathbb{E}[ \ell(\gamma, f_\hat{\theta} (z)) ] \end{aligned}\]لاحظ ان المخاطر هي توقع لمتغير عشوائي وليست عشوائية بحد ذاتها. القيمة المتوقعة من رمي حجر النرد ذو الست جهات بشكل عادل وعشوائي هي 3.5 على الرغم من أن عمليات الرمي نفسها عشوائية.
المثال السابق يطلق عليه أحياناً المخاطر الحقيقة True Risk لأنها تخبرنا عن أداء النموذج على كامل المجتمع الإحصائي. إذا تمكنا من إيجاد المخاطر الحقيقة لجميع النماذج، يمكننا ببساطة اختيار النموذج الأقل مخاطر ونكون متأكدين أن النموذج سيكون أداة أفضل من بقية النماذج على المدى البعيد على دالة الخسارة التي اخترناها.
الخطر التجريبي
الواقع ليس بهذه السهولة والروعة. إذا قمنا بتغير تعريف التوقع إلى معادة المخاطر الحقيقة، سنحصل على التالي:
\[\begin{split} \begin{aligned} R(f_\hat{\theta}) &= \mathbb{E}[ \ell(\gamma, f_\hat{\theta} (z)) ] \\ &= \sum_\gamma \sum_z \ell(\gamma, f_\hat{\theta} (z)) P(\gamma, z) \\ \end{aligned} \end{split}\]للتبسيط، نريد أن نعرف ما تعنيه $ P(\gamma, z) $، وهي توزيع الاحتمالية العام لأي من النقاط في المجتمع الإحصائي. للأسف، إيجاد ذلك ليس سهلاً. لنفترض أننا نريد أن نتوقع قيمة الإكرامية بناءًا على عدد العملاء في الطاولة. ما هي احتمالية أن طاولة بثلاث أشخاص يقومون بإعطاء إكرامية بقيمة $14.50؟ إذا كنا نعرف توزيع النقاط بشكل دقيقة، فلا نحتاج لجمع بيانات وضبط النموذج، سيكون لدينا معرفة بالقيمة المحتملة للإكرامية لأي عدد من العملاء في الطاولة.
على الرغم أننا لا نعرف بشكل دقيق توزيع المجتمع الإحصائي، يمكننا توقعه بناءًا على ما أطلعنا عليه في البيانات $ X $ و $ y $. إذا قمنا بسحب قيم ل $ X $ و $ y $ بشكل عشوائي من المجتمع الإحصائي، توزيع النقاط في $ X $ و $ y $ سيكون مشابه لتوزيع المجتمع الإحصائي. لذا، نعامل $ X $ و $ y $ كمجتمعنا الإحصائي. لذا، احتمالية الظهور لأي من المدخلات والمخرجات $ X_i $ و $ y_i $ هي $ \frac{1}{n} $ بما أن كل كلاهما يظهر مرة واحدة من بين كل النقاط $ n $.
ذلك يسمح لنا بحساب الخطر التجريبي Empirical Risk، قيمة تقريبه للخطر الحقيقي:
\[\begin{split} \begin{aligned} \hat R(f_\hat{\theta}) &= \mathbb{E}[ \ell(y_i, f_\hat{\theta} (X_i)) ] \\ &= \sum_{i=1}^n \ell(y_i, f_\hat{\theta} (X_i)) \frac{1}{n} \\ &= \frac{1}{n} \sum_{i=1}^n \ell(y_i, f_\hat{\theta} (X_i)) \end{aligned} \end{split}\]إذا كانت البيانات لدينا ذات حجم كبير وتم سحبها بشكل عشوائي من المجتمع الإحصائي، فإن الخطر التجريبي $ \hat R(f_\hat{\theta}) $ سيكون قريب جداً من الخطر الحقيقي $ R(f_\hat{\theta}) $. يسمح لنا ذلك باختيار النموذج الذي يقلل من الخطر التجريبي.
لاحظ أن هذا المصطلح هو متوسط دالة الخسارة في بداية هذا الجزء! بالتقليل من متوسط الخسارة، فأننا أيضاً نقلل من الخطر التجريبي. يوضح ذلك لماذا نستخدم في العادة متوسط الخسارة كنتيجة لدالة الخسارة بدلاً مثلاً من أعلى قيمة للخسارة.
ملخص المخاطر
الخطر الحقيقي لتنبؤ النموذج يوضح لنا خسارة النموذج على المدى البعيد التي سيحصل عليها من المجتمع الإحصائي. بما أننا عادةً لا نستطيع حساب الخطر الحقيقي بشكل مباشر، فأننا نقوم بحساب الخطر التجريبي ونستخدمه لإيجاد النموذج المناسب لتوقعنا. لأن الخطر التجريبي هو متوسط الخسارة على البيانات التي رأيناها، فأننا عادةً نقلل من متوسط الخسارة عند ضبط النماذج.
انحياز وتباين النموذج
رأينا سابقاً أن لدينا مصدرين لاتخاذ قرار الأفضلية بين النماذج.
النموذج قد يكون بسيط جداً. مثلاً، نموذج خطي بسيط لن يتمكن من ضبط البيانات إذا كانت من الدرجة الثانية. يظهر هذا الخطأ بسبب الانحياز Bias في النموذج. 📝 📝
النموذج قد يقوم بضبط البيانات العشوائية الموجودة في البيانات، حتى لو قمنا بضبط بيانات من الدرجة الثانية على نموذج مماثل، سيتوقع النموذج نتائج مختلفة عن الصحيحة. هذا الخطأ يظهر في النموذج بسبب التباين Variance. 📝 📝
تحليل الانحياز والتباين
يمكننا تحليل التعريفات السابقة وفهمها بشكل أوضح باستخدام معادلة مخاطر النموذج. لنتذكر أن المخاطر Risk للنموذج $ f_\hat{\theta} $ هي الخسارة المتوقعة لجميع بيانات التدريب $ X $ و $ y $ وجميع النقاط المدخلة والمخرجة $ z, \gamma $ في المجتمع الإحصائي:
\[\begin{aligned} R(f_\hat{\theta}) = \mathbb{E}[ \ell(\gamma, f_\hat{\theta} (z)) ] \end{aligned}\]نرمز لعملية إنشاء بيانات المجتمع الإحصائي الحقيقة ب $ f_\theta(x) $. القيمة الناتجة $ \gamma $ تنتج بواسطة بيانات المجتمع الإحصائي اضافة لقيمة عشوائية مشوشة من البيانات: $ \gamma_i = f_\theta(z_i) + \epsilon $. التشويش العشوائي Random Noise $ \epsilon $ هي قيمة عشوائية لديها متوسط يساوي صفر: $ \mathbb{E}[\epsilon] = 0 $. 📝 📝
إذا استخدمنا الخطأ التربيعي كدالة الخسارة، تصفح المعادلة السابقة كالتالي:
\[\begin{aligned} R(f_\hat{\theta}) = \mathbb{E}[ (\gamma - f_\hat{\theta} (z))^2 ] \end{aligned}\]مع قليل من عمليات المعالجة الجبرية، يمكن أن نعرف المعادلة السابقة كالتالي:
\[\begin{aligned} R(f_\hat{\theta}) = (\mathbb{E}[f_\hat{\theta}(z)] - f_\theta(z))^2 + \text{Var}(f_\hat{\theta}(z)) + \text{Var}(\epsilon) \end{aligned}\]المصطلح الأول في المعادلة، $ (\mathbb{E}[f_\hat{\theta}(z)] - f_\theta(z))^2 $، هي التعبير الرياضي للانحياز في النموذج. (يمكننا القول تقنياً إن المصطلح هو تربيع الانحياز $ \text{bias}^2 $ ). الانحياز سيساوي صفر على المدى البعيد إذا كان اختيارنا للنموذج $ f_\hat{\theta}(z) $ يتوقع نفس النتائج التي تم نتجت من خطوات معالجة المجتمع الإحصائي $ f_\theta(z) $. يكون الانحياز عالي إذا كان النموذج الذي اخترناه يتوقع نتائج خاطئة في خطوات معالجة المجتمع الإحصائي حتى لو كانت كامل المجتمع الإحصائي كبيانات تدريب.
المصطلح الثاني في المعادلة، $ \text{Var}(f_\hat{\theta}(z)) $، هو تباين النموذج. يكون التباين أقل عندما تكون توقعات النموذج لا تتغير كثيراً عند تدريبه على بيانات مختلفة من المجتمع الإحصائي. يكون التباين عالي عندما يكون التغير كبير عند تدريبه على بيانات مختلفة من المجتمع الإحصائي.
المصطلح الأخير في المعادلة، $ \text{Var}(\epsilon) $، يعني الخطأ الغير قابل للإختزال أو التشويش الناتج عند بناء البيانات أو جمعها. يكون أقل عندما يكون بناء البيانات وجمعها دقيق. والعكس يكون أعلى عندما يكون التشويش عالي في البيانات.
مشتقة تحليل الانحياز والتبيان
أولاً، نبدأ بمتوسط الخطأ التربيعي:
\[\mathbb{E}[(\gamma - f_{\hat{\theta}}(z))^2]\]ثم نوسع التربيع ونطبق خطية التوقع Linearity of Expectation:
\[=\mathbb{E}[\gamma^2 -2\gamma f_{\hat{\theta}} +f_\hat{\theta}(z)^2\] \[= \mathbb{E}[\gamma^2] - \mathbb{E}[2\gamma f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2]\]لأن $ \gamma $ و $ f_{\hat{\theta}}(z) $ مستقلان (نتائج النموذج وما اطلع عليه من المجتمع الإحصائي لا يعتمدان على بعضهما)، يمكننا القول إن $ \mathbb{E}[2\gamma f_{\hat{\theta}}(z)] = \mathbb{E}[2\gamma] \mathbb{E}[f_{\hat{\theta}}(z)] $. ثم نقوم بتعويض $ f_\theta(z) + \epsilon $ بدلاً من $ \gamma $:
\[=\mathbb{E}[(f_\theta(z) + \epsilon)^2] - \mathbb{E}[2(f_\theta(z) + \epsilon)] \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2]\]للتبسيط أكثر: (لاحظ أن $ \mathbb{E}[f_\theta(z)] = f_\theta(z) $ لأن $ f_\theta(z) $ دالة حتمية، إذا أعطيت نقطة معينة $ z $.)
\[=\mathbb{E}[f_\theta(z)^2 + 2f_\theta(z) \epsilon + \epsilon^2] - (2f_\theta(z) + \mathbb{E}[2\epsilon]) \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2]\]تطبيق خطية التوقع مرة أخرى:
\[= f_\theta(z)^2 + 2f_\theta(z)\mathbb{E}[\epsilon] + \mathbb{E}[\epsilon^2] - (2f_\theta(z) + 2\mathbb{E}[\epsilon]) \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2]\]لاحظ أن $ \big( \mathbb{E}[\epsilon] = 0 \big) => \big( \mathbb{E}[\epsilon^2] = \text{Var}(\epsilon) \big) $ لأن $ \text{Var}(\epsilon) = \mathbb{E}[\epsilon^2]-\mathbb{E}[\epsilon]^2 $:
\[= f_\theta(z)^2 + \text{Var}(\epsilon) - 2f_\theta(z) \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2]\]يمكننا الآن إعادة كتابة المعادلة كالتالي:
\[= f_\theta(z)^2 + \text{Var}(\epsilon) - 2f_\theta(z) \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)^2] - \mathbb{E}[f_{\hat{\theta}}(z)]^2 + \mathbb{E}[f_{\hat{\theta}}(z)]^2\]لأن $ \mathbb{E}[f_{\hat{\theta}}(z)^2] - \mathbb{E}[f_{\hat{\theta}}(z)]^2 = Var(f_{\hat{\theta}}(z)) $:
\[= f_\theta(z)^2 - 2f_\theta(z) \mathbb{E}[f_{\hat{\theta}}(z)] + \mathbb{E}[f_{\hat{\theta}}(z)]^2 + Var(f_{\hat{\theta}}(z)) + \text{Var}(\epsilon)\] \[= (f_\theta(z) - \mathbb{E}[f_{\hat{\theta}}(z)])^2 + Var(f_{\hat{\theta}}(z)) + \text{Var}(\epsilon)\] \[= \text{bias}^2 + \text{model variance} + \text{noise}\]لاختيار نموذج يؤدي بشكل ممتاز، نسعى دائماً أن نحصل على مخاطر أقل. ولتقليلها، نحاول تقليل الانحياز، التباين والتشويش. تقليل التشويش يتطلب عادةً تحسين في طريقة جمع البيانات. للتقليل من الانحياز والتباين، يجب علينا ضبط النماذج وتعقيدها. النماذج البسيطة يكون فيها الانحياز مرتفع؛ النماذج المعقدة جداً لديها تباين عالي. هذا هو مفهوم المقايضة بين الانحياز والتباين bias-variance tradeoff، مشكلة أساسية نواجهها دائماً عند اختيار نماذج التنبؤ.
مثال: الإنحدار الخطي وموجات الجيب Sine Waves
لنفترض أننا نحاول إنشاء نموذج للدالة المتأرجحة التالية:
from collections import namedtuple
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
np.random.seed(42)
Line = namedtuple('Line', ['x_start', 'x_end', 'y_start', 'y_end'])
def f(x): return np.sin(x) + 0.3 * x
def noise(n):
return np.random.normal(scale=0.1, size=n)
def draw(n):
points = np.random.choice(np.arange(0, 20, 0.2), size=n)
return points, f(points) + noise(n)
def fit_line(x, y, x_start=0, x_end=20):
clf = LinearRegression().fit(x.reshape(-1, 1), y)
return Line(x_start, x_end, clf.predict([[x_start]])[0], clf.predict([[x_end]])[0])
population_x = np.arange(0, 20, 0.2)
population_y = f(population_x)
avg_line = fit_line(population_x, population_y)
datasets = [draw(100) for _ in range(20)]
random_lines = [fit_line(x, y) for x, y in datasets]
قام الكاتب في الكود البرمجي السابق إنشاء بيانات عشوائية لغرض العمل عليها في هذا الجزء من الدرس، الناتج من هذا الكود يظهر في الرسم البياني التالي
plt.plot(population_x, population_y)
plt.title('True underlying data generation process');
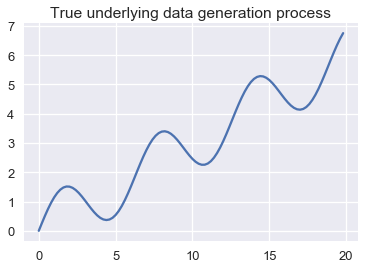
إذا حاولنا أخذ مجموعه بيانات من المجتمع الإحصائي في هذه الرسم، قد نصل إلى الشكل التالي:
xs, ys = draw(100)
plt.scatter(xs, ys, s=10)
plt.title('One set of observed data');
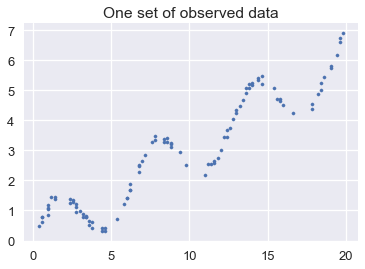
لنفترض أننا قمنا بسحب مجموعات مختلفة من البيانات من هذا المجتمع الإحصائي وقمنا بضبط نموذج خطي بسيط لكل مجموعة. في الأسفل، قمنا برسم شكل خطي لبيانات المجتمع الإحصائي الناتجة باللون الأزرق و توقعات النموذج باللون الأخضر:
plt.figure(figsize=(8, 5))
plt.plot(population_x, population_y)
for x_start, x_end, y_start, y_end in random_lines:
plt.plot([x_start, x_end], [y_start, y_end], linewidth=1, c='g')
plt.title('Population vs. linear model predictions');
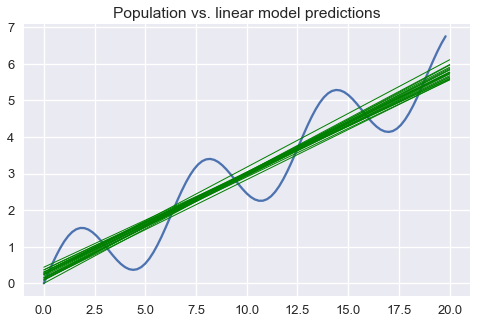
الرسم البياني السابق يوضح أن توقع النموذج الخطي سينتج أخطاء. يمكننا حل هذه الأخطاء باستخدام الانحياز، التباين والتشويش الغير قابل للإختزال. نوضح الانحياز في نموذجنا عن طريق إظهار أن متوسط النموذج الخطي على المدى البعيد سيتوقع نتائج مختلفة عن تلك في المجتمع الإحصائي:
plt.figure(figsize=(8, 5))
xs = np.arange(0, 20, 0.2)
plt.plot(population_x, population_y, label='Population')
plt.plot([avg_line.x_start, avg_line.x_end],
[avg_line.y_start, avg_line.y_end],
linewidth=2, c='r',
label='Long-run average linear model')
plt.title('Bias of linear model')
plt.legend();
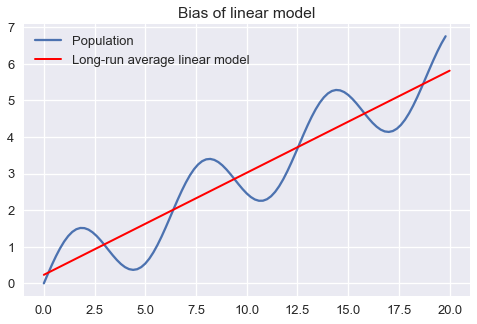
التباين للنموذج هو مدى اختلاف توقعات النموذج حول متوسط النموذج على المدى البعيد:
plt.figure(figsize=(8, 5))
for x_start, x_end, y_start, y_end in random_lines:
plt.plot([x_start, x_end], [y_start, y_end], linewidth=1, c='g', alpha=0.8)
plt.plot([avg_line.x_start, avg_line.x_end],
[avg_line.y_start, avg_line.y_end],
linewidth=4, c='r')
plt.title('Variance of linear model');
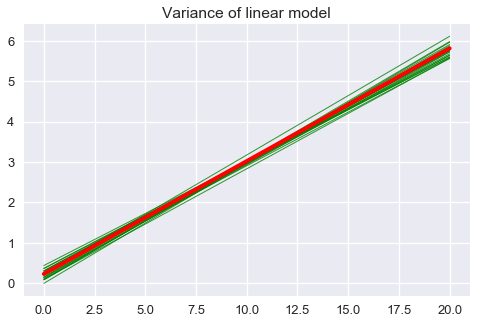
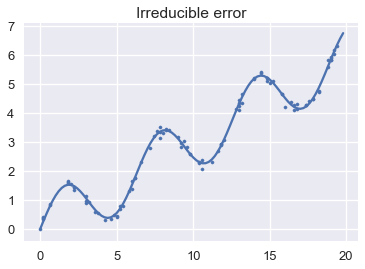
أخيراً، نستعرض الخطأ الغير قابل للإختزال عن طريق إظهار انحراف النقاط في بيانات المجتمع الإحصائي:
plt.plot(population_x, population_y)
xs, ys = draw(100)
plt.scatter(xs, ys, s=10)
plt.title('Irreducible error');
التطبيق العملي للانحياز والتباين
في عالمٍ مثالي، نقوم بالتقليل من الخطأ المتوقع من تنبؤ النموذج لجميع النقاط الداخلة والخارجة في المجتمع الإحصائي. ولكن، عملياً، نحن لا نعرف خطوات بناء البيانات ولذلك لن نستطيع بشكل دقيق تحديد انحياز، تباين والخطأ الغير قابل للإختزال للنموذج. بدلاً من ذلك، نستخدم البيانات التي مرت علينا وقيمه قريبه لما في المجتمع الإحصائي.
كما رأينا في الأعلى، الوصول إلى قيمة أقل للخطأ في بيانات التدريب لا يعني أن النموذج سيحصل على قيمه أقل أيضاً في بيانات الاختبار. من السهل الحصول على نموذج بقيمة انحياز قليله جداً وبالتالي قيمة خطأ أقل في بيانات التدريب عن طريق ضبط النموذج باستخدام منحنى يمر على جميع بيانات التدريب. ولكن هذا النموذج سيكون تباينه عالي جداً والذي يؤدي إلى خطأ عالي في بيانات الاختبار. على العكس، النموذج الذي يتوقع قيمه ثابتة لدية تباين أقل و انحياز عالي. أساساً، يحدث ذلك بسبب أن خطأ التدريب يعكس انحياز النموذج ولكن ليس تباينه؛ ولكن خطأ الاختبار يعكس كليهما. للتقليل من خطأ الاختبار، يحتاج نموذجنا أن يحقق انحياز وتباين قليلان معاً. للقيام بذلك، نحتاج لطريقة لمحاكاة خطأ الاختبار دون استخدام بيانات الاختبار. يتم ذلك عادةً باستخدام التحقق المتقاطع Cross-Validation.
النقاط الأساسية
المقايضة بين الانحياز والتباين تسمح لنا بشكل دقيق وصف ظواهر النماذج التي رأيناها سابقاً.
يحدث فرط التعميم Underfitting عادةً بسبب الانحياز؛ فرط التخصيص يحدث بسبب التباين.
جمع المزيد من البيانات يقلل من التباين. مثلاً، تباين نموذج الانحدار الخطي يقل بمعدل عامل $ 1/n $، هنا $ n $ هي عدد النقاط في البيانات. لذا، مضاعفة حجم البيانات يقلل التباين إلى النصف، وسحب المزيد من البيانات سيقلل التباين إلى صفر. إحدى الخطوات الشائعة هي اختيار نموذج بانحياز قليل وتباين عالي (مثلاً شبكة عصبيه) ومن ثم سحب المزيد من البيانات للتقليل من تباين النموذج إلى ان يصل لقيمه قليله تمكنه من القيام بتوقعات صحيحه. على الرغم فاعليتها عملياً، إلى أن جمع المزيد من البيانات لهذه النماذج عادةً ما يأخذ وقت و جهد ومصاريف أكثر.
جمع المزيد من البيانات يقلل الانحياز إذا تم ضبط النموذج على بيانات المجتمع الإحصائي كاملة. إذا لم نتمكن من ضبط النموذج على كامل المجتمع الإحصائي (كما في المثال السابق)، حتى لو كان لدينا عدد لا نهائي من البيانات لن نتمكن من التخلص من الانحياز.
إضافة خصائص Features مفيدة للبيانات، مثلاً التربيع عندما تكون البيانات الأساسية من الدرجة الثانية، تقلل من الانحياز. إضافة خصائص غير مفيدة نادراً منا تزيد من الانحياز.
إضافة خصائص سواء كانت مفيدة أم لا، عادةً ما تزيد من التباين كون كل خاصية نضيفها تزيد من المتغيرات في النموذج. بشكل عام، النماذج ذات المتغيرات الكثيرة لديها أشكال مختلفة من المتغيرات ولذلك لديها تباين أعلى من نماذج بمتغيرات أقل. للزيادة من دقة توقعات النموذج، إضافة خاصية جديده يجب أن تقلل من الانحياز أكثر مما تزيد من التباين.
حذف الخصائص عادةً ما يزيد من الانحياز وقد يتسبب بفرط التعميم. مثلاً، نموذج خطي بسيط لديه انحياز أعلى من نفس النموذج إذا أضيفت له خاصية تربيعية. إذا تم إنشاء البيانات باستخدام التربيع، فإن النموذج الخطي البسيط سيتناسب مع البيانات.
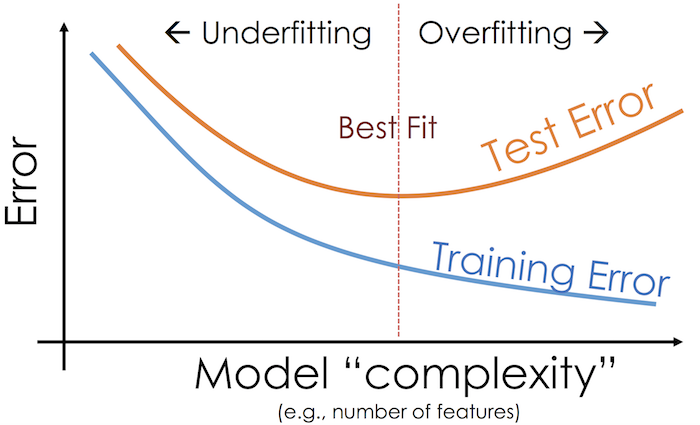
في الرسم البياني التالي، المحور السيني يقيس تعقيد النموذج والمحور الصادي يقيس حجمه. لاحظ أنه كلما زاد تعقيد النموذج، يقل الانحياز بشكل واضح وبينما يزيد التباين بنفس الشكل. عندما نختار نموذجاً معقد، خطأ الاختبار في البداية يقل ثم يزيد حتى يصل تباين النموذج ويتجاوز الانحياز أثناء هبوطه:
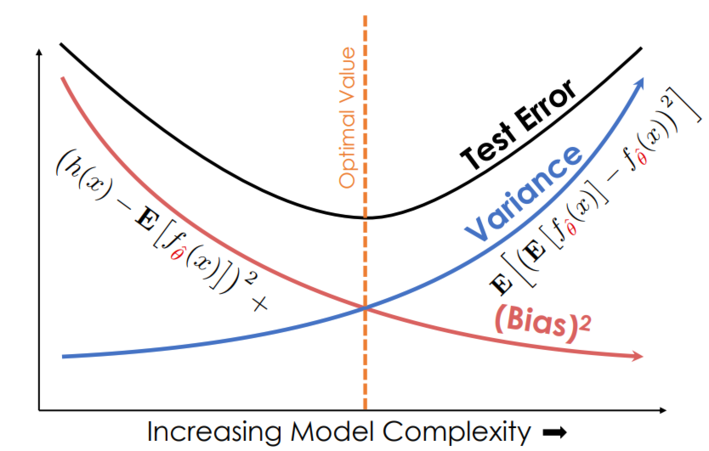
كما هو واضح في الرسم، النموذج ذو التعقيد العالي قد يصل إلى خطأ قليل في بيانات التدريب ولكن قد يفشل في تعميم هذه النتائج على بيانات الاختبار بسبب تباينه العالي. بشكل آخر، النموذج بتعقيد أقل سيكون ذو تباين أقل ولكن قد يفشل أيضاً في التعميم بسبب انحيازه العالي. لاختيار النموذج المفيد، يجب أن نصل إلى التوازن بين انحياز وتباين النموذج.
كلما أضفنا المزيد إلى البيانات، نقوم بتحريك المنحنى في رسمنا البياني إلى اليمين والأسفل، نقلل من الانحياز والتباين:
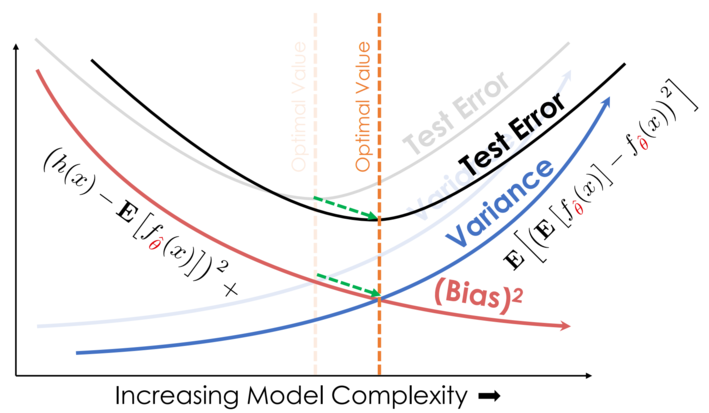
ملخص انحياز وتباين النموذج
مقايضة الانحياز والتبيان تكشف لنا عن مشكلة أساسية في النمذجة. من أجل التقليل من مخاطر النموذج، فعلينا أن نستخدم مزيجاً من هندسة الخصائص، اختيار النماذج والتحقق المتقاطع للوصول إلى توازن بين الانحياز والتباين.
التحقق المتقاطع
في الجزء السابق، رأينا أننا نحتاج لطريقة أدق لمحاكاة خطأ الاختبار للتحكم بالمقايضة بين الانحياز والتباين. للتأكيد، خطأ التدريب قليل جداً، لأننا نضبط النموذج على بيانات التدريب. نريد اختيار نموذج دون الحاجة لاستخدام بيانات الاختبار، لذا نقسم بيانات التدريب مرة أخرى إلى بيانات تحقق. يسمح لنا التحقق المتقاطع Cross-validation بتوقع خطأ النموذج باستخدام بيانات يطلع عليها مرة واحدة عن طريق فصل بين البيانات المستخدمة في التدريب والبيانات المستخدمة لاختيار النموذج ودقته. 📝
تقسيم بيانات التدريب والتحقق والاختبار
إحدى الطرق لتطبيق ذلك على البيانات هي تقسيمها إلى ثلاث أقسام:
- بيانات التدريب: البيانات التي ستستخدم لضبط النموذج.
- بيانات التحقق: البيانات التي ستستخدم لاختيار الخصائص.
- بيانات الاختبار: البيانات التي ستقرر النتيجة النهائية لدقة النموذج.
بعد التقسيم، نختار الخصائص والنموذج بناءًا على:
- لكل خاصية محتملة في البيانات، نقوم بضبطها على النموذج باستخدام بيانات التدريب. الخطأ في هذا النموذج هو خطأ التدريب Training Error.
- تحقق من كل نتيجة خطأ لكل نموذج في بيانات التحقق: يطلق على ذلك خطأ التحقق Validation Error. قم باختيار النموذج صاحب أقل خطأ تحقق. سيكون ذلك هو الخيار النهائي للنموذج وخصائصه.
- قم بحساب خطأ الاختبار Test Error، الخطأ في النموذج النهائي على بيانات الاختبار. هذه هي الدقة النهائية للنموذج. محظور لنا من التعديل الخصائص أو النموذج للتقليل من خطأ الاختبار؛ فعل ذلك سيحول بيانات الاختبار إلى بيانات تحقق. بدلاً من ذلك، يجب علينا جمع بيانات جديده للاختبار بعد القيام بالتعديلات على الخصائص أو النموذج.
تسمح لنا هذه الخطوات بشكل دقيق من تحديد النموذج الذي نريد استخدامه بدلاً من استخدام خطأ التدريب وحده. باستخدام التحقق المتقاطع، يمكننا اختبار النموذج على بيانات لم يتم ضبطه عليها، محاكاة خطأ الاختبار دون استخدام بيانات الاختبار. يسمح لنا ذلك بمعرفة قدرة النموذج على التعامل مع بيانات لم يرها من قبل.
حجم تقسيم بيانات التدريب والتحقق والاختبار
تقسيم بيانات التدريب والتحقق والاختبار عادة ما يكون فيه 70% بيانات تدريب، 15% بيانات تحقق وال 15% الباقية بيانات اختبار. الزيادة في عدد بيانات التدريب يساعد على رفع دقة النموذج ولكنه يسبب مزيداً من الاختلاف في بيانات التحقق والاختبار. ذلك بسبب أن بيانات التحقق والاختبار ذات الحجم الصغير غير كافيه لتمثيل البيانات.
خطأ التدريب و خطأ الاختبار
النموذج يكون غير مفيد لنا إذا فشل في التعامل مع بيانات من المجتمع الإحصائي لم يرها من قبل. خطأ الاختبار يقدم لنا أدق تمثيل لأداء النموذج على بيانات جديده كوننا لا نستخدم بيانات الاختبار في تدريب النموذج أو اختيار الخصائص.
بشكل عام، يقل خطأ التدريب كلما أضفنا تعقيداً أكثر للنموذج بإضافة المزيد من الخصائص أو خطوات معقدة في التوقع. خطأ الاختبار، يقل حتى نقطة معينة ثم يزيد إلى أن يتم ضبطه على بيانات التدريب. ذلك بسبب أنه في البداية، الانحياز يقل أكثر من زيادة التباين. في النهاية، تتجاوز الزيادة في التباين النزول في الانحياز.
التحقق المتقاطع K-Flod
طريقة تقسيم بيانات التدريب والتحقق والاختبار جيدة لمحاكاة نتيجة خطأ الاختبار باستخدام بيانات التحقق. ولكن، عند التقسيم سيكون حجم البيانات أقل في التدريب. أيضاً، بهذه الطريقة قد يكون خطأ التحقق يميل إلى الزيادة في التباين بسبب أن تقييم الخطأ قد يعتمد بشكل كبير على مكان تواجد القيم في بيانات التدريب أو التحقق.
لمواجهة هذه المشكلة، يمكننا تطبيق تقيم التدريب والتحقق أكثر من مرة على نفس البيانات. يتم تقسيم البيانات إلى تقسيمات بعدد k متساوية في الحجم (a$ k $ تقسيمات) ، ويتم اعادة تقسيم التدريب والتحقق بعدد k مرات. في كل مرة، إحدى التقسيمات في k تستخدم كبيانات تحقق، والقيم المتبقية k-1 تستخدم كبيانات تدريب. نقوم بتحديد النتيجة النهائية لخطأ التحقق للنموذج بإيجاد متوسط خطأ التحقق في كل تقسيم. يطلق على هذه الطريقة بـ K-Flod التحقق المتقاطع K-Flod cross-validation. 📝
الرسم التالي يشرح الطريقة عند استخدامها التقسيم 5 مرات:
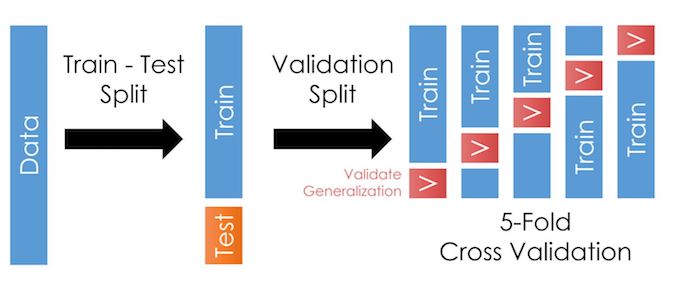
ما يميز هذه الطريقة أن كل نقطة في البيانات تستخدم مرة واحد فقط في بيانات التحقق و في بيانات التدريب k-1 مرات. عادةً، تكون k بين 5 و 10، ولكن تبقى قيمة k غير ثابتة. عندما تكون k رقماً صغيراً، الخطأ يكون تباينه قليلاً (الكثير من بيانات التحقق) ولكن لدية انحياز عالي (القليل من بيانات التدريب). على العكس، عندما تكون قيمة k عالية قيمة الخطأ تكون أقل تحيزاً ولكن تباينها عالي.
التحقق المتقاطع a$ k $-flod يأخذ وقتاً أطول من تقسيم بيانات التدريب والتحقق في عملية الحساب لأننا عادةً نحتاج لإعادة ضبط كل نموذج مع كل عملية تقسيم. ولكن، عملية الحساب تعطي نتائج أكثر دقة لخطأ التحقق عن طريق حساب متوسط أكثر من قيمة خطأ لكل نموذج.
مكتبة scikit-learn توفر طريقة جاهزة sklearn.model_selection.KFold لتطبيق التحقق المتقاطع a$ k $-flod.
مقايضة الانحياز والتباين
يساعدنا التحقق المتقاطع في التحكم بمقايضة الانحياز والتباين بشكل أكثر دقة. حدسياً، خطأ التحقق يقيم خطأ الاختبار عن طريق التحقق من أداء النموذج على بيانات لم تستخدم في التدريب؛ يسمح لنا ذلك بتوقع انحياز وتباين النموذج. التحقق المتقاطع K-flod يظهر أيضاً حقيقة أن التشويش في بيانات الاختبار فقط تأثر على التشويش في مصطلح الانحياز والتباين بينما التشويش في بيانات التدريب يؤثر على الانحياز وتباين النموذج. لاختيار النموذج النهائي للبدء باستخدامه، نختار النموذج ذو قيمة خطأ تحقق أقل.
مثال: اختيار النموذج لبيانات تقييم الآيس كريم
سنتعرف على عملية اختيار النموذج الكاملة، بالإضافة للتحقق المتقاطع، لاختيار نموذج يتوقع تقييم الآيس كريم بناءًا على حلاوة نكهة الآيس كريم. جميع بيانات الآيس كريم إضافة لمخطط التشتت والتقييم العام بالإضافة إلى حلاوة نكهة الآيس كريم هي كالتالي:
لتحميل البيانات icecream.csv اضغط هنا.
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
ice = pd.read_csv('icecream.csv')
transformer = PolynomialFeatures(degree=2)
X = transformer.fit_transform(ice[['sweetness']])
clf = LinearRegression(fit_intercept=False).fit(X, ice[['overall']])
xs = np.linspace(3.5, 12.5, 300).reshape(-1, 1)
rating_pred = clf.predict(transformer.transform(xs))
temp = pd.DataFrame(xs, columns = ['sweetness'])
temp['overall'] = rating_pred
np.random.seed(42)
x_devs = np.random.normal(scale=0.2, size=len(temp))
y_devs = np.random.normal(scale=0.2, size=len(temp))
temp['sweetness'] = np.round(temp['sweetness'] + x_devs, decimals=2)
temp['overall'] = np.round(temp['overall'] + y_devs, decimals=2)
ice = pd.concat([temp, ice])
ice
| overall | sweetness | |
|---|---|---|
| 3.09 | 3.6 | 0 |
| 3.17 | 3.5 | 1 |
| 3.46 | 3.69 | 2 |
| … | … | … |
| 5.9 | 11 | 6 |
| 5.5 | 11.7 | 7 |
| 5.4 | 11.9 | 8 |
309 rows × 2 columns
في الكود البرمجي السابق قام الكاتب بتوليد بيانات عشوائية مقاربة للبيانات الأصلية في ملف ice.csv
plt.scatter(ice['sweetness'], ice['overall'], s=10)
plt.title('Ice Cream Rating vs. Sweetness')
plt.xlabel('Sweetness')
plt.ylabel('Rating');
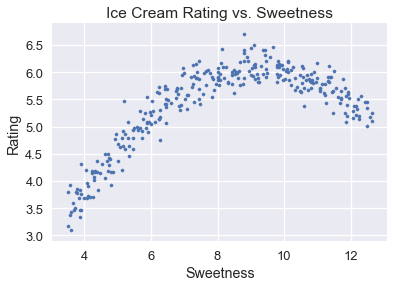
باستخدام خصائص متعددة الحدود من الدرجة العاشرة على 9 مدخلات في ملف البيانات تكون لنا نموذج مثالي لتلك النقاط. للأسف، سيفشل هذا النموذج في التعميم لبيانات لم يراها من قبل في المجتمع الإحصائي:
ice2 = pd.read_csv('icecream.csv')
trans_ten = PolynomialFeatures(degree=10)
X_ten = trans_ten.fit_transform(ice2[['sweetness']])
y = ice2['overall']
clf_ten = LinearRegression(fit_intercept=False).fit(X_ten, y)
np.random.seed(1)
x_devs = np.random.normal(scale=0.4, size=len(ice2))
y_devs = np.random.normal(scale=0.4, size=len(ice2))
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(ice2['sweetness'], ice2['overall'])
xs = np.linspace(3.5, 12.5, 1000).reshape(-1, 1)
ys = clf_ten.predict(trans_ten.transform(xs))
plt.plot(xs, ys)
plt.title('Degree 10 polynomial fit')
plt.ylim(3, 7);
plt.subplot(122)
ys = clf_ten.predict(trans_ten.transform(xs))
plt.plot(xs, ys)
plt.scatter(ice2['sweetness'] + x_devs,
ice2['overall'] + y_devs,
c='g')
plt.title('Degree 10 poly, second set of data')
plt.ylim(3, 7);
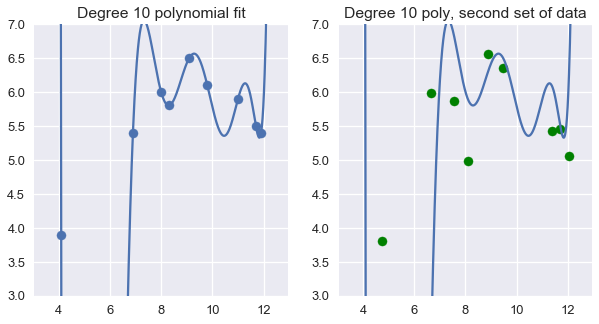
بدلاً من الطريقة السابقة، أولاً نقسم البيانات إلى تدريب، تحقق واختبار باستخدام الدالة sklearn.model_selection.train_test_split من مكتبة scikit-learn للقيام بفصل يساوي 70/30% تدريب-اختبار.
from sklearn.model_selection import train_test_split
test_size = 92
X_train, X_test, y_train, y_test = train_test_split(
ice[['sweetness']], ice['overall'], test_size=test_size, random_state=0)
print(f' Training set size: {len(X_train)}')
print(f' Test set size: {len(X_test)}')
Training set size: 217
Test set size: 92
نقوم الآن بضبط نماذج الانحدار متعددة الحدود باستخدام بيانات التدريب، واحد لكل درجة في متعددة الحدود من 1 إلى 10.
# أولاً، نظيف خصائص متعددة الحدود إلى X_train
transformers = [PolynomialFeatures(degree=deg)
for deg in range(1, 11)]
X_train_polys = [transformer.fit_transform(X_train)
for transformer in transformers]
# عرض X_train
# مع متجهة خصائص من الدرجة الخامسة
X_train_polys[4]
array([[ 1. , 8.8 , 77.44, 681.47, 5996.95, 52773.19],
[ 1. , 10.74, 115.35, 1238.83, 13305.07, 142896.44],
[ 1. , 9.98, 99.6 , 994.01, 9920.24, 99003.99],
...,
[ 1. , 6.79, 46.1 , 313.05, 2125.59, 14432.74],
[ 1. , 5.13, 26.32, 135.01, 692.58, 3552.93],
[ 1. , 8.66, 75. , 649.46, 5624.34, 48706.78]])
ثم نقوم بتطبيق التحقق المتقاطع ب 5 تقسيمات على البيانات العشرة. للقيام بذلك، سنقوم بتعريف دالة تقوم بالتالي:
- استخدام
KFold.splitللحصول على 5 تقسيمات في بيانات التدريب. لاحظ أنsplitتعود لنا بمؤشراتindicesللبيانات في ذلك الفصل. - لكل عملية فصل، استخرج لنا الأسطر والأعمدة بناءاً على مؤشرات الفصل
indicesوالخصائص. - اضبط النموذج الخطي على بيانات التدريب المقسمة.
- احسب متوسط الخطأ التربيعي في بيانات التحقق المقسمة.
- أوجد لنا متوسط الخطأ لكل تقسيمات التحقق المتقاطع.
from sklearn.model_selection import KFold
def mse_cost(y_pred, y_actual):
return np.mean((y_pred - y_actual) ** 2)
def compute_CV_error(model, X_train, Y_train):
kf = KFold(n_splits=5)
validation_errors = []
for train_idx, valid_idx in kf.split(X_train):
# تقسيم البيانات
split_X_train, split_X_valid = X_train[train_idx], X_train[valid_idx]
split_Y_train, split_Y_valid = Y_train.iloc[train_idx], Y_train.iloc[valid_idx]
# ضبط النموذج على تقسيمة التدريب
model.fit(split_X_train,split_Y_train)
# حساب متوسط الخطأ التربيعي على بيانات التحقق
error = mse_cost(split_Y_valid,model.predict(split_X_valid))
validation_errors.append(error)
# متوسط خطأ بيانات التحقق جميعها
return np.mean(validation_errors)
# قمنا بتدريب نموذج إنحدار خطي لكل البيانات وطبقنا التحقق المتقاطع
# حددنا fit_intercept=False
# في نموذج الإنحدار الخطي لأن محول PolynomialFeatures
# يقوم بإضافة عمود الانحياز بدلاً عنا.
cross_validation_errors = [compute_CV_error(LinearRegression(fit_intercept=False), X_train_poly, y_train)
for X_train_poly in X_train_polys]
cv_df = pd.DataFrame({'Validation Error': cross_validation_errors}, index=range(1, 11))
cv_df.index.name = 'Degree'
pd.options.display.max_rows = 20
display(cv_df)
pd.options.display.max_rows = 7
| Validation Error | |
|---|---|
| Degree | |
| 0.32482 | 1 |
| 0.04506 | 2 |
| 0.045418 | 3 |
| 0.045282 | 4 |
| 0.046272 | 5 |
| 0.046715 | 6 |
| 0.04714 | 7 |
| 0.04754 | 8 |
| 0.048055 | 9 |
| 0.047805 | 10 |
يمكن أن نلاحظ أنه عندما نرفع قيمة درجة متعددة الحدود، تقل قيمة خطأ التحقق وتزيد مرة أخرى:
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.plot(cv_df.index, cv_df['Validation Error'])
plt.scatter(cv_df.index, cv_df['Validation Error'])
plt.title('Validation Error vs. Polynomial Degree')
plt.xlabel('Polynomial Degree')
plt.ylabel('Validation Error');
plt.subplot(122)
plt.plot(cv_df.index, cv_df['Validation Error'])
plt.scatter(cv_df.index, cv_df['Validation Error'])
plt.ylim(0.044925, 0.05)
plt.title('Zoomed In')
plt.xlabel('Polynomial Degree')
plt.ylabel('Validation Error')
plt.tight_layout();
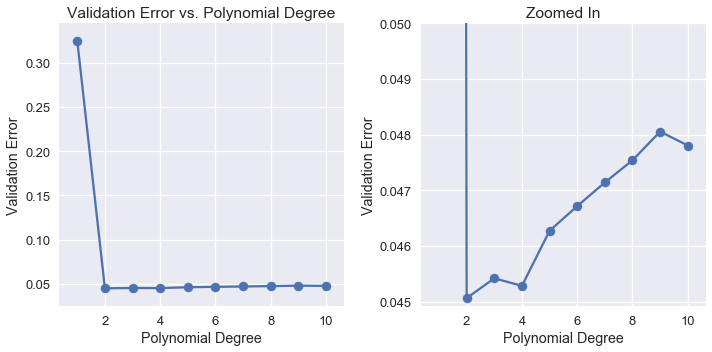
عند مراجعة نتائج خطأ التحقق يظهر لنا أن النموذج المثالي أستخدم خصائص متعددة الحدود من الدرجة الثانية. لذا، نختار نموذج متعددة الحدود من الدرجة الثانية كنموذجنا النهائي وضبطه على جميع بيانات التدريب. ثم نقوم بحساب خطأ النموذج على بيانات الاختبار:
best_trans = transformers[1]
best_model = LinearRegression(fit_intercept=False).fit(X_train_polys[1], y_train)
training_error = mse_cost(best_model.predict(X_train_polys[1]), y_train)
validation_error = cross_validation_errors[1]
test_error = mse_cost(best_model.predict(best_trans.transform(X_test)), y_test)
print('Degree 2 polynomial')
print(f' Training error: {training_error:0.5f}')
print(f'Validation error: {validation_error:0.5f}')
print(f' Test error: {test_error:0.5f}')
Degree 2 polynomial
Training error: 0.04409
Validation error: 0.04506
Test error: 0.04698
للتطبيق مستقبلاً، توفر مكتبة scikit-learn طريقة cross_val_predict للقيام أوتوماتيكياً بالتحقق المتقاطع، لذا لا نحتاج أن نقوم بأنفسنا بفصل بيانات التدريب والتحقق. 📝
أيضاً، لاحظ أن خطأ الاختبار أعلى من خطأ التحقق والذي أيضاً أعلى من خطأ التدريب. خطأ التدريب يجب أن يكون الأقل لأن النموذج تم ضبطه على بيانات التدريب. ضبط النموذج يقلل من متوسط الخطأ التدريبي للبيانات. خطأ التحقق والاختبار عادةً ما تكون أعلى من خطأ التدريب لأن حساب الخطأ فيها تم على بيانات غير معروفة ولم يسبق أن رآها في النموذج.
ملخص التحقق المتقاطع
استخدمنا الوسيلة المفيدة دائماً التحقق المتقاطع للتحكم بمقايضة الانحياز والتباين. بعد حساب فصل بيانات التدريب، التحقق والاختبار على البيانات الأصلية، نستخدم الخطوات التالية لتدريب واختيار النموذج:
- لكل مجموعة من الخصائص، نقوم بضبط بيانات التدريب عليها. خطأ النموذج على بيانات التدريب هو خطأ التدريب Training Error.
- تحقق من الخطأ لكل نموذج في بيانات التحقق باستخدام التحقق المتقاطع a$ k $-flod cross validation: الخطأ هنا هو خطأ التحقق Validation Error. نختار النموذج الذي حقق أقل قيمة في خطأ التحقق. هنا نكون قد اخترنا خياراتنا النهائية لخصائص النموذج.
- نحسب خطأ الاختبار Test Error، خطأ النموذج النهائي على بيانات الاختبار. هذه آخر خطوه لمعرفة دقة النموذج. يجب ألا نقوم بأي تعديل في النموذج لزيادة خطأ الاختبار؛ القيام بذلك يحول بيانات الاختبار إلى بيانات تحقق. عند القيام بذلك، نحتاج لجمع بيانات اختبار جديده بعد القيام بأي تعديلات في النموذج.