مبادئ وتقنيات علم البيانات
الفصل السادس: تصوير البيانات
فهرس الفصل:
مقدمة
هناك سحر في الرسوم البيانية. المنحنى في الرسم يظهر بشكل سريع الحالة — قصة حياة وباء، الهلع، أو مرحلة الرخاء. المنحنى ينبه العقل، يثير الخيال، يقنعه.
التصوير والرسوم البيانية أداه أساسية في كل خطوه من خطوات التحليل في علم البيانات، من التنظيف حتى التحليل الاستكشافي للبيانات إلى الوصول لنتائج وتوقعات. لأن العقل البشري متطور للغاية للإدراك البصري، اختيار الرسم البياني الصحيح يظهر لنا الاتجاهات والشذوذ في البيانات بشكل أفضل من الوصف النصي.
لتستخدم تصوير البيانات بشكل فعال، يجب أن تكون خبيراً في أدوات البرمجة التي تنشئ الرسوم البيانية ومبادئ تصوير ورسم البيانات. في هذا الفصل سنتعرف على seaborn و matplotlib، الأدوات التي اخترناها للرسم. سنتعلم أيضا كيف نكتشف الرسوم البيانية المضللة وكيف نحسن ممن الرسوم البيانية باستخدام تحويل، تبسيط، وتقليل أبعاد البيانات.
البيانات الكمية
تصوير البيانات الكمية
عادة ما نستخدم أنواع مختلفة من الرسوم البيانية لتصوير البيانات الكمية (الرقمية) والنوعية (الاسمية).
في البيانات الكمية، عادة ما نستخدم المدرج التكراري Histogram، مخطط الصندوق Box Plot، ومخطط التشتت Scatter Plot.
يمكننا استخدام مكتبة Seaborn للرسوم البيانية لرسم تلك الرسوم في بايثون. سنستخدم بيانات تحتوي على معلومات رُكاب سفينة تايتانيك.
# جلب المكتبه
import seaborn as sns
# تطبيق الإعدادات الإفتراضيه لثيم Seaborn
sns.set()
# تحميل وتعريف البيانات وحذف الحقول الفارغه
ti = sns.load_dataset('titanic').dropna().reset_index(drop=True)
df_interact(ti)
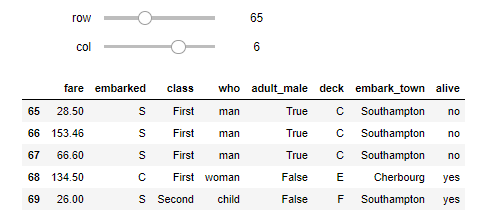
(182 rows, 15 columns) total
كما في الفصل السابق، عرف الكاتب دالة تقوم بإظهار أجزاء من البيانات مع إمكانية التنقل بينها بواسطة الشريطين في الأعلى
import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual def df_interact(df): def peek(row=0, col=0): return df.iloc[row:row + 5, col:col + 8] interact(peek, row=(0, len(df), 5), col=(0, len(df.columns) - 6)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1]))
المدرج التكراري
نرى أن كل سطر في البيانات هو معلومات لراكب. كل سطر يحتوي على عمر الراكب والقيمة التي دفعها على التذكرة. لنرسم عمود العمر باستخدام المدرج التكراري. يمكننا استخدام دالة distplot الموجودة في Seaborn:
# اضافة ; في النهاية تخبر جوبتر أن لا يظهر النتيجة التاليه
# <matplotlib.axes._subplots.AxesSubplot>
# بل يظهر لنا الرسم البياني مباشره
sns.distplot(ti['age']);
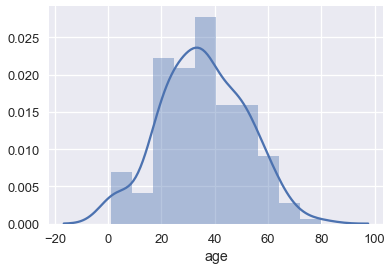
بشكل تلقائي، دالة distplot في Seaborn ستُظهر منحنى يناسب توزيع البيانات لدينا. يمكننا إظهار Rug Plot والتي تقوم بتحديد أماكن توزيع البيانات على المحور x :
sns.distplot(ti['age'], rug=True);
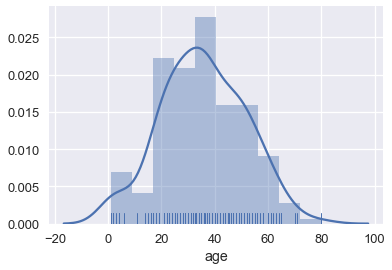
يمكننا أيضا التحكم بالتوزيع. بالتعديل على عدد البيانات لكل مجموعة:
sns.distplot(ti['age'], kde=False, bins=30);
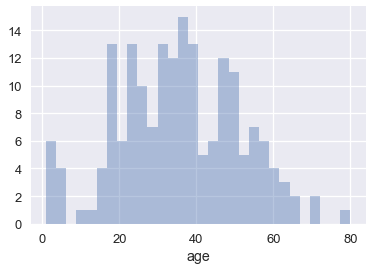
مخطط الصندوق
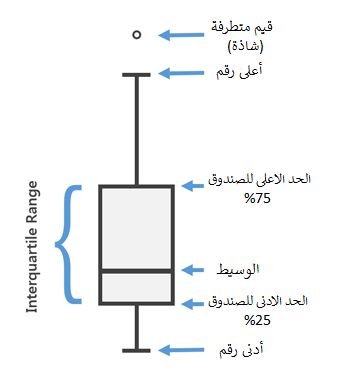
يعتبر مخطط الصندوق طريقة مناسبة لمعرفة أين تجتمع البيانات. عادةً، نستخدم النسبة 25 و 75 كنقطتي بداية ونهاية للصندوق ونرسم خطاً عند النسبة 50 (المتوسط)، نرسم خارجها خطين لبقية البيانات دون القيم المتطرفة والتي يرمز لها بنقاط خارج الخطين.
يمكن تبسيط مخطط الصندوق بالرسمه التاليه:
مصدر الصورة
sns.boxplot(x='fare', data=ti);
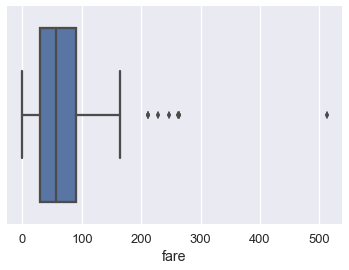
عادةً ما يستخدم الانحراف الربيعي Inter-Quartile Range (IQR) لتحديد أي النقاط يمكن حسابها كنقاط شاذة في مخطط الصندوق. IQR هو الفرق بين بيانات النسبة 75 و 25:
lower, upper = np.percentile(ti['fare'], [25, 75])
iqr = upper - lower
iqr
60.299999999999997
القيم اكبر من $ 1.5 \times \text{IQR} $ تكون أعلى من نسبة 75% والقيم أقل من $ 1.5 \times \text{IQR} $ تكون أسفل النسبة 25% ويتم اعتبارها قيم شاذة ويمكننا مشاهدتها في الرسم البياني لمخطط الصندوق السابق:
upper_cutoff = upper + 1.5 * iqr
lower_cutoff = lower - 1.5 * iqr
upper_cutoff, lower_cutoff
(180.44999999999999, -60.749999999999986)
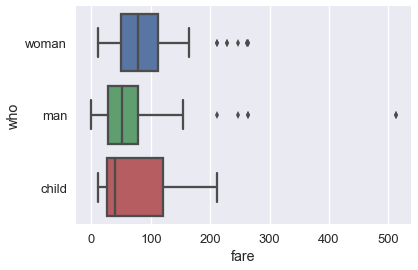
بالرغم أن المدرج التكراري يظهر كل البيانات مرة واحدة، يسهل علينا فهم مخطط الصندوق عندما نقسمه حسب نوع البيانات. مثلاً، يمكننا رسم مخطط الصندوق لكل نوع من الرُكاب:
sns.boxplot(x='fare', y='who', data=ti);
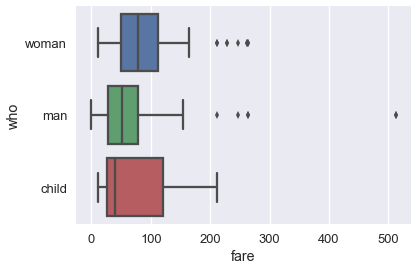
يسهل علينا فهم مخطط الصندوق عند تقسيمه على عكس المدرج التكراري، التالي رسم لنفس البيانات وتقسيمها ولكن في مدرج تكراري:
sns.distplot(ti.loc[ti['who'] == 'woman', 'fare'])
sns.distplot(ti.loc[ti['who'] == 'man', 'fare'])
sns.distplot(ti.loc[ti['who'] == 'child', 'fare']);
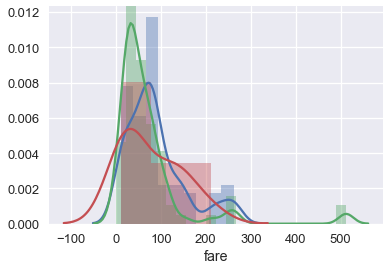
نقطة بسيطه عن استخدام مكتبة Seaborn
ربما لاحظت أن الدالة boxplot أنشأت مخطط صندوق منفصل لكل نوع داخل العمود who وكانت أسهل للكتابة على عكس طريقة الرسم في المدرج التكراري. على الرغم مان sns.distplot تستقبل البيانات كمصفوفات، الكثير من الدوال في Seaborn يمكنها قبول البيانات التي على شكل DataFrame ونحدد أي الأعمدة على المحورين x و y. مثلاً:
# ارسم العمود fare في بيانات ti على المحور x
sns.boxplot(x='fare', data=ti);

عندما تكون نوع البيانات في العمود نوعية ( العمود 'who' يحتوي على 'women', 'men' و 'child')، مكتبة Seaborn ستقوم أوتوماتيكيا بتقسيم البيانات حسب نوعها قبل رسمها. لذا لا نحتاج لفلترة البيانات حسب نوعها كما فعلنا في الدالة sns.distplot:
# fare (رقمي) على المحور x
# who (نوعي) على المحور y
sns.boxplot(x='fare', y='who', data=ti);
مخطط التشتت
مخطط التشتت يستخدم للمقارنة بين قيمتين كمية (رقمية). يمكننا المقارنة بين العامودان age و fare في بيانات تايتانيك:
sns.lmplot(x='age', y='fare', data=ti);
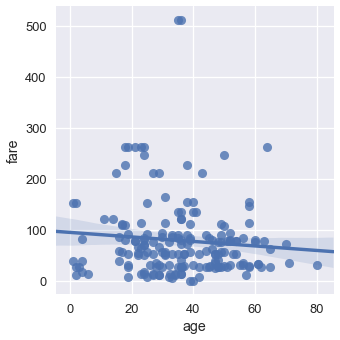
بشكل تلقائي تقوم Seaborn بإضافة خط الانحدار للرسم البياني ومجال ثقة حول خط الانحدار والذي يظهر بلون ازرق شفاف. في حالتنا هذه لا يبدو أن خط الانحدار صحيح لذا سنقوم بإخفائه: 📝
sns.lmplot(x='age', y='fare', data=ti, fit_reg=False);
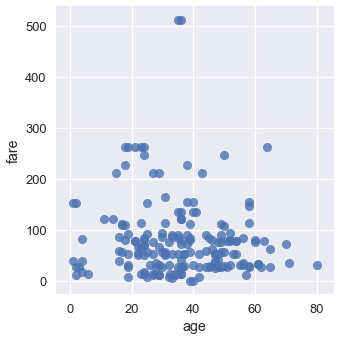
يمكننا تلوين النقاط حسب نوعها. لنستخدم العمود who مرة أخرى:
sns.lmplot(x='age', y='fare', hue='who', data=ti, fit_reg=False);
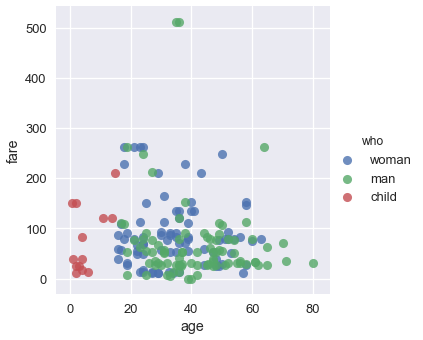
من الرسم البياني السابق يمكننا ملاحظة أن أكثر الرُكاب دون ال18 سنة تم تحديدهم كأطفال child. لا يبدو أن هناك فرق في سعر التذكرة fare بين الذكور والإناث، على الرغم أن أعلى تذكرتين سعراً تم شرائها من قبل ذكران.
البيانات النوعية
تصوير البيانات النوعية
للبيانات النوعية أو التصنيفية، عادة ما نستخدم المخطط الشريطي Bar Chart أو النقطي Dot Chart. سنرى كيف بإمكاننا رسم هذه الرسوم البيانية باستخدام seaborn وبيانات الناجين من سفينة تايتانيك:
import seaborn as sns
sns.set()
# تحميل البيانات
ti = sns.load_dataset('titanic').reset_index(drop=True)
df_interact(ti)
(891 rows, 15 columns) total
المخطط الشريطي
في seaborn، يوجد نوعين من المخططات الشريطية. النوع الأول يستخدم دالة countplot ليقوم بعد عدد مرات تكرار كل نوع في العمود:
# يقوم برسم وحساب عدد الناجين والذين لم ينجو ثم رسم شريط بعددهم
sns.countplot(x='alive', data=ti);
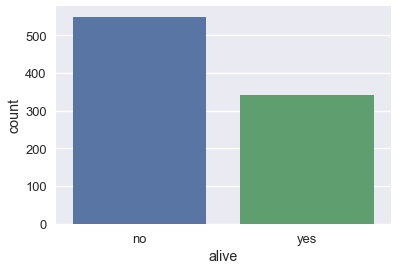
sns.countplot(x='class', data=ti);
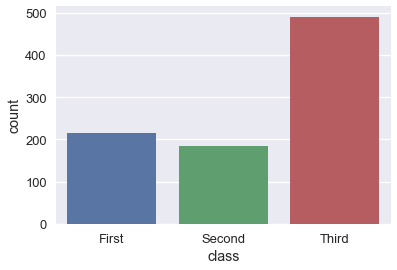
# كما في مخطط الصندوق، يمكننا التقسيم بشكل اوسع باستخدام الألوان
sns.countplot(x='alive', hue='class', data=ti);
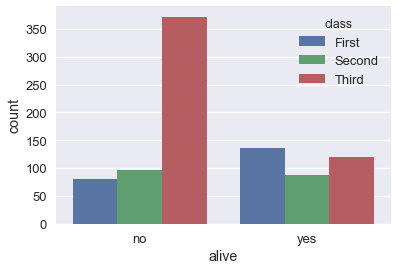
والطريقة الأخرى، دالة barplot، تجمع البيانات باستخدام عمود نوعي ويتم تحديد طول الشريط بِنَاءًا على متوسط نتيجة عمود كمي لكل نوع من الأنواع.
# لكل نوع ناجي/لم ينجو، قم بحساب ورسم متوسط الأعمار
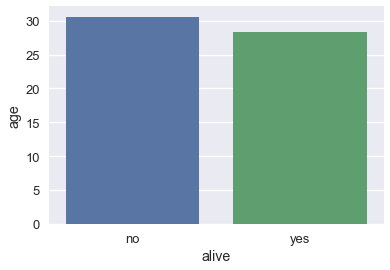
sns.barplot(x='alive', y='age', data=ti);
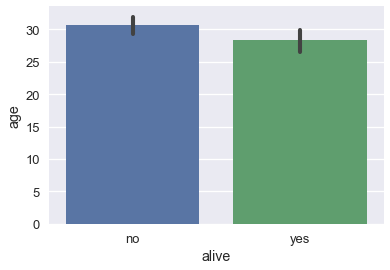
يمكننا حساب طول كل شريط عن طريق جمع الأعمدة alive و age وحساب المتوسط للعمود age:
ti[['alive', 'age']].groupby('alive').mean()
| Age | |
|---|---|
| alive | |
| 30.626179 | no |
| 28.343690 | yes |
بشكل تلقائي، دالة barplot تحاول حساب فاصل ثقة بنسبة 95% باستخدام Bootstrap لكل متوسط. مشار إليها بالخط الأسود في أعلى الشريط. فاصل الثقه يحاول توضيح أنه إذا كانت بيانات تايتانيك تحتوي على عينة عشوائية، الفرق في عمر الراكب بين الذين نجو والذين لم ينجو ليس مهم إحصائياً على مستوى 5%.
فواصل الثقة تأخذ وقتاً طويلاً للحساب عندما يكون لدينا بيانات ذات حجم أكبر، لذا من الأفضل عدم حسابها:
sns.barplot(x='alive', y='age', data=ti, ci=False);
المخطط النقطي
المخطط النقطي يتشابه كثيراً مع المخطط الشريطي. بدلاً من رسم أشرطة، المخطط النقطي يرسم نقطة واحدة تعبر عن نهاية الشريط. نستخدم الدالة pointplot في seaborn لرسم المخطط النقطي. كما في barplot، دالة pointplot تقوم بالتجميع أوتوماتيكياً وحساب المتوسط لعمود رقمي، وتحديد فاصل ثقة بنفسه 95% بخطوط عاموديه يكون النقطة متوسطها:
# لكل نوع ناجي/لم ينجو، قم بحساب ورسم متوسط الأعمار
sns.pointplot(x='alive', y='age', data=ti);
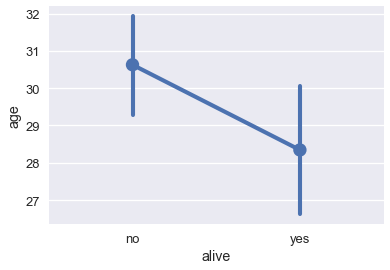
المخطط النقطي مفيد جداً عند محاولة مقارنة التغيرات على حسب نوع البيانات:
# عرض نسبة الناجين بناءًا على الفئة
sns.pointplot(x='class', y='survived', data=ti);
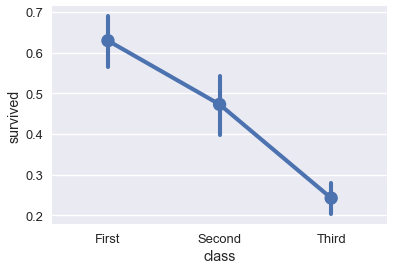
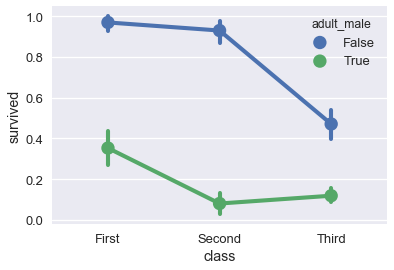
# عرض نسبة الناجين بناءًا على الفئة
# التقسيم ما اذا كان الناجي ذكر بالغ
sns.pointplot(x='class', y='survived', hue='adult_male', data=ti);
تخصيص الرسوم البيانية
تخصيص الرسوم البيانية باستخدام matplotlib
على الرغم ان seaborn تُمكنا من رسم العديد من أنواع الرسوم البيانية بشكل سريع، لكنها لا يمكننا التحكم بشكل كامل بالرسم. مثلاً، لا يمكننا في seaborn تعديل عنوان الرسم البياني، وعناوين محاور الطول والعرض، أو إضافة ملاحظات على الرسم. لذا، يجب علينا استخدام مكتبة matplotlib والتي تعتمد عليها seaborn
مكتبة
seabornهي بالأساسmatplotlibولكن أضيفت لها تحسينات وتعديلات لتتمكن من التعامل مع مكتبةpandas.
توفر لنا matplotlib الأساسيات لإنشاء الرسوم البيانية في بايثون. على الرغم من أنها تمكنا من الحصول على تحكم كامل، إلا أنها أيضاً متعبة في العمل، إعادة رسم ما رسمناه سابقاً في seaborn باستخدام matplotlib سنحتاج لكتابة العديد من الأسطر البرمجية. بالأصح، يمكننا القول إن seaborn هي اختصار مفيد لإنشاء رسوم بيانية في matplotlib. نفضل العمل بالرسوم المبدئية المقدمة من seaborn، ولكن لتعديل وتخصيص الرسومات لغرض النشر سنحتاج لمعرفة أساسيات العمل في matplotlib.
قبل أن نرى المثال الأول، يجب علينا تفعيل دعم مكتبة matplotlib في Jupyter Notebook.
# هذا السطر يجعل الرسوم البيانية تظهر كصور في جوبتر بدلاً من ان تظهر في صفحة منفصلة
%matplotlib inline
# الاختصار plt هو اختصار كثير الأستخدام لمكتبة matplotlib
import matplotlib.pyplot as plt
تخصيص الرسم والأبعاد
للرسم في matplotlib، نحتاج أولاً لإنشاء شكل بياني أو Figure، ثم إضافة المحاور Axes للشكل. في matplotlib، المحور Axes هو رسم بياني واحد، والشكل البياني Figure يمكن أن يحتوي على عدة محاور على شكل جداول. المحور يحتوي على نقاط Marks، وهي الخطوط أو النقاط المرسومة في الرسم البياني:
# انشاء الشكل البياني
f = plt.figure()
# اضافة محور إلى الشكل البياني. المتغير الثاني والثالث تقوم بإنشاء
# جدول بسطر وعمود واحد. المتغير الاول يتحكم بمكان المحور، هنا في الخليه الأولى
ax = f.add_subplot(1, 1, 1)
# انشاء رسم بياني خطي على المحور
ax.plot([0, 1, 2, 3], [1, 3, 4, 3])
# أظهار الرسم البياني، في جوبتر يتم نداء هذه الدالة بشكل اوتوماتيكي
# لذا لن نستخدمها في الأكواد البرمجية القادمة
plt.show()
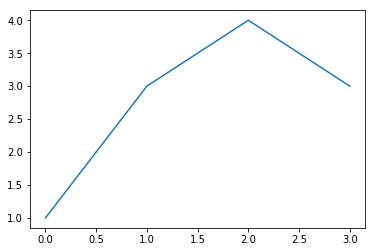
للتخصيص في هذه الرسمه، يمكننا استخدام دوال أخرى على كائن المحور:
كائن هنا تعني Object
f = plt.figure()
ax = f.add_subplot(1, 1, 1)
x = np.arange(0, 10, 0.1)
# اضافة المتغير label تمكننا من انشاء عنوان للخط
ax.plot(x, np.sin(x), label='sin(x)')
ax.plot(x, np.cos(x), label='cos(x)')
ax.legend()
ax.set_title('Sinusoids')
ax.set_xlabel('x')
ax.set_ylabel('y');
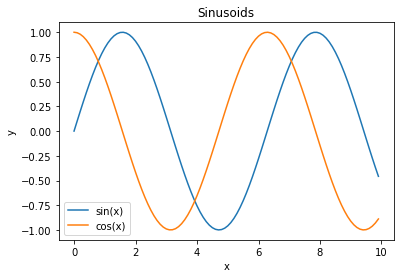
كاختصار، matplotlib لديها دوال رسم بياني في plt يمكنها إنشاء شكل بياني ومحور أوتوماتيكياً:
# اختصار لرسم شكل بياني ومحور
plt.plot(x, np.sin(x))
# عند استخدام plt اكثر من مره في نفس الخليه، سيتم إعادة استخدام نفس الشكل والمحور
plt.scatter(x, np.cos(x));
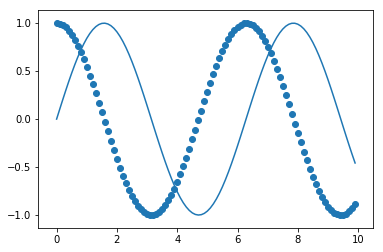
يحتوي plt على دوال مشابهة للتي في المحور، لذا يمكننا إعادة إنشاء أحد الرسوم في الأعلى باستخدام plt مباشره:
x = np.arange(0, 10, 0.1)
plt.plot(x, np.sin(x), label='sin(x)')
plt.plot(x, np.cos(x), label='cos(x)')
plt.legend()
# اختصار ل ax.set_title
plt.title('Sinusoids')
plt.xlabel('x')
plt.ylabel('y')
# تحديد مقاسات محوري x و y
plt.xlim(-1, 11)
plt.ylim(-1.2, 1.2);
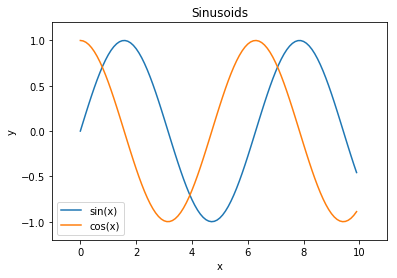
تخصيص النقاط
لتغير خصائص النقاط في الرسمه ( مثلاً، الخطوط في الرسمه السابقة)، يمكننا تمرير المزيد من المتغيرات إلى plt.plot: 📝
plt.plot(x, np.sin(x), linestyle='--', color='purple');
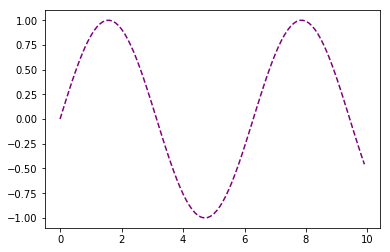
تصفح الشرح الخاص بمكتبة matplotlib هو أسهل طريقة لمعرفة أي المتغيرات متوفرة لكل دالة. الطريقة الأخرى هي حفظ الكائن الناتج عن دالة الرسم: 📝
line = plt.plot([1,2,3])
كائن الخط في الرسم البياني يحتوي على الكثير من الخصائص التي يمكن أن تتحكم فيها، يمكن عرضها باستخدام .set، هذه قائمة كاملة بخصائص الرسم البياني السابق:
line.set
line.set line.set_drawstyle line.set_mec
line.set_aa line.set_figure line.set_mew
line.set_agg_filter line.set_fillstyle line.set_mfc
line.set_alpha line.set_gid line.set_mfcalt
line.set_animated line.set_label line.set_ms
line.set_antialiased line.set_linestyle line.set_picker
line.set_axes line.set_linewidth line.set_pickradius
line.set_c line.set_lod line.set_rasterized
line.set_clip_box line.set_ls line.set_snap
line.set_clip_on line.set_lw line.set_solid_capstyle
line.set_clip_path line.set_marker line.set_solid_joinstyle
line.set_color line.set_markeredgecolor line.set_transform
line.set_contains line.set_markeredgewidth line.set_url
line.set_dash_capstyle line.set_markerfacecolor line.set_visible
line.set_dashes line.set_markerfacecoloralt line.set_xdata
line.set_dash_joinstyle line.set_markersize line.set_ydata
line.set_data line.set_markevery line.set_zorder
ولكن استخدام setp (اختصار لتحديد خاصية) قد يكون أفضل، خاصة عند العمل بشكل تفاعلي كونه يحتوي على وصف، لكي تتعلم الطرق الصحيحة لنداء الدوال أثناء عملك عليها:
line = plt.plot([1,2,3])
plt.setp(line, 'linestyle')
linestyle: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
plt.setp(line)
agg_filter: unknown
alpha: float (0.0 transparent through 1.0 opaque)
animated: [True | False]
antialiased or aa: [True | False]
...
...
...
في النتيجة الأولى يظهر لنا القيم الصحيحة التي يقبلها متغير linestyle، وفي النتيجة الثانية يظهر لنا جميع المتغيرات التي يمكن تخصيصها في كائن الخط. يمكنك ذلك بسهولة اكتشفت وتخصيص رسومك البيانية لتحصل على ما تريده.
النصوص ودعم LaTeX
في matplotlib يمكن إضافة النص لمحور معين أو للشكل البياني ككل.
هذه الأوامر لإضافة نصوص للمحاور:
- set_title: إضافة عنوان
- set_xlabel: إضافة عنوان للمحور السيني x-axis
- set_ylabel: إضافة عنوان للمحور الصادي y-axis
- text: إضافة نص في مكان معين
- annotate: إضافة ملاحظة مع إمكانية إضافة سهم
والأوامر التالية للشكل البياني:
- figtext: إضافة نص في مكان معين
- suptitle: إضافة عنوان
وأي نص من الممكن أن يحتوي على نصوص بشكل LaTeX والمخصصة للعمليات الرياضية، طالما تم إضافتها بداخل علامتي $.
هذا المثال على جميع ما سبق:
fig = plt.figure()
fig.suptitle('bold figure suptitle', fontsize=14, fontweight='bold')
ax = fig.add_subplot(1, 1, 1)
fig.subplots_adjust(top=0.85)
ax.set_title('axes title')
ax.set_xlabel('xlabel')
ax.set_ylabel('ylabel')
ax.text(3, 8, 'boxed italics text in data coords', style='italic',
bbox={'facecolor':'red', 'alpha':0.5, 'pad':10})
ax.text(2, 6, 'an equation: $E=mc^2$', fontsize=15)
ax.text(3, 2, 'unicode: Institut für Festkörperphysik')
ax.text(0.95, 0.01, 'colored text in axes coords',
verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes,
color='green', fontsize=15)
ax.plot([2], [1], 'o')
ax.annotate('annotate', xy=(2, 1), xytext=(3, 4),
arrowprops=dict(facecolor='black', shrink=0.05))
ax.axis([0, 10, 0, 10]);

تخصيص رسوم seaborn باستخدام matplotlib
والآن بعد أن رأينا كيف نستخدم matplotlib لتخصيص الرسم البياني، يمكننا استخدام نفس الدوال للتخصيص في seaborn لأن seaborn تقوم بإنشاء الرسوم البيانية باستخدام matplotlib:
# تحميل مكتبة seaborn
import seaborn as sns
sns.set()
# ضبط شكل وحجم الرسم
# https://seaborn.pydata.org/generated/seaborn.set_context.html
sns.set_context('talk')
# تحميل البيانات
ti = sns.load_dataset('titanic').dropna().reset_index(drop=True)
ti.head()
| alone | alive | embark_town | deck | … | age | sex | pclass | survived | |
|---|---|---|---|---|---|---|---|---|---|
| FALSE | yes | Cherbourg | C | … | 38 | female | 1 | 1 | 0 |
| FALSE | yes | Southampton | C | … | 35 | female | 1 | 1 | 1 |
| TRUE | no | Southampton | E | … | 54 | male | 1 | 0 | 2 |
| FALSE | yes | Southampton | G | … | 4 | female | 3 | 1 | 3 |
| TRUE | yes | Southampton | C | … | 58 | female | 1 | 1 | 4 |
5 rows × 15 columns
لنبدأ بهذه الرسمه:
sns.lmplot(x='age', y='fare', hue='who', data=ti, fit_reg=False);
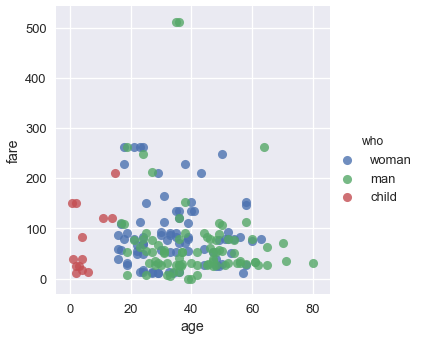
يمكننا رؤية أن الرسم يحتاج لعنوان وصف أفضل لعناوين المحورين x و y. أيضاً، الشخصين اللذين لديهما أعلى التذاكر سعراً نجا، لذا نحتاج لإضافة توضيح ذلك في رسمنا البياني:
sns.lmplot(x='age', y='fare', hue='who', data=ti, fit_reg=False)
plt.title('Fare Paid vs. Age of Passenger, Colored by Passenger Type')
plt.xlabel('Age of Passenger')
plt.ylabel('Fare in USD')
plt.annotate('Both survived', xy=(35, 500), xytext=(35, 420),
arrowprops=dict(facecolor='black', shrink=0.05));
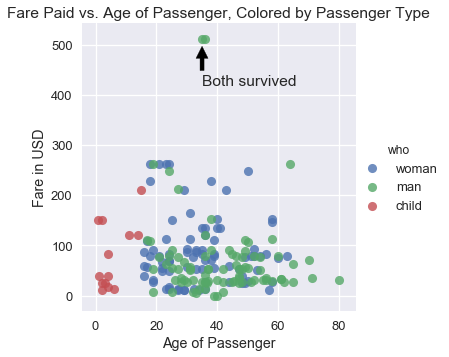
بشكل عملي، سنستخدم seaborn لتصفح البيانات بشكل سريع ثم ننتقل إلى matplotlib لنحسن من الرسوم بعد اختيارنا للرسم البياني المثالي.
مبادئ تصوير البيانات
والآن بما أن لدينا الأدوات لرسم وتخصيص الرسوم البيانية، ننتقل للمبادئ الأساسية لتصوير البيانات. تماماً كما في باقي أقسام علم البيانات، من الصعب تحديد مقاييس معينة لكفاءة رسمه بيانية معينة. لكن، هناك مبادئ أساسيه وجودها يجعل الرسوم البيانية فعالة بشكل كبير ويظهر اتجاهات البيانات. سنناقش ست مبادئ: المقياس، الحالة، الإدراك، التحويل، النصوص والتبسيط.
مبادئ المقاييس
يقصد بمبادئ المقاييس هو اختيار المقاسات المناسبة للمحاور x و y في الرسم البياني.
في جلسة استماع في الكونجرس الأمريكي عام 2015، الوكيل شافيتز ناقش تحقيق عن برنامج Planned Parenthood. قام الوكيل باستخدام الرسم البياني التالي والذي ظهر في تقرير من قبل مؤسسة Americans United for Life. يقارن الرسم بين اجراءات الإجهاض و فحوص السرطان، كلا الإجرائين يتم تقديمها في Planned Parenthood. (التقرير متوفر بشكل كامل هنا).
ما المريب بهذا الرسم البياني؟ كم نقطة تم رسمها؟

هذا الرسم يخالف مبادئ المقاييس، لا يحسن الاختيار لمحوري x و y.
عندما نختار المحورين x و y في رسمنا البياني، يجب أن نبقي مقاساتنا ثابتة على طول المحور. ولكن، الرسمه العلوية تحتوي على مقاسين مختلفين لخطي إجراءات الإجهاض وفحوص السرطان، بداية خط إجراءات الإجهاض ونهاية خط فحوص السرطان يبدوان قريبين من بعضهما على المحور y ولكن الأرقام تظهر العكس. أيضاً، تم رسم النقاط لسنتي 2006 و 2013 ولكن المحور x يحتوي على علامات إضافية لسنوات بينهما ولم يتم استخدامها.
للتحسين من هذا الرسم البياني، يجب علينا إعادة رسم النقاط على مقاس ثابت في المحور y:
لتحميل بيانات Planned Parenthood اضغط هنا.
pp = pd.read_csv("data/plannedparenthood.csv")
plt.plot(pp['year'], pp['screening'], linestyle="solid", marker="o", label='Cancer')
plt.plot(pp['year'], pp['abortion'], linestyle="solid", marker="o", label='Abortion')
plt.title('Planned Parenthood Procedures')
plt.xlabel("Year")
plt.ylabel("Service")
plt.xticks([2006, 2013])
plt.legend();
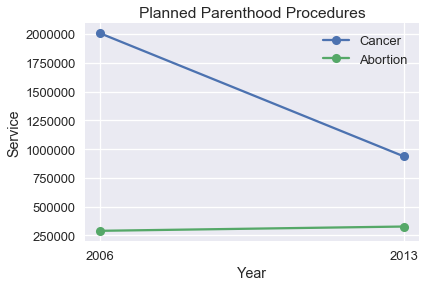
يمكن أن نلاحظ أن الفرق في إجراءات الإجهاض قليل مقارنة بالنزول المفاجئ في فحوص السرطان. بدلاً من مقارنة عدد الإجراءات بينهما، ربما من الأفضل مقارنة فرق بالنسبة بين السنتين 2006 و 2013:
percent_change = pd.DataFrame({
'percent_change': [
pp['screening'].iloc[1] / pp['screening'].iloc[0] - 1,
pp['abortion'].iloc[1] / pp['abortion'].iloc[0] - 1,
],
'procedure': ['cancer', 'abortion'],
'type': ['percent_change', 'percent_change'],
})
ax = sns.barplot(x='procedure', y='percent_change', data=percent_change)
plt.title('Percent Change in Number of Procedures')
plt.xlabel('')
plt.ylabel('Percent Change')
plt.ylim(-0.6, 0.6)
plt.axhline(y=0, c='black');
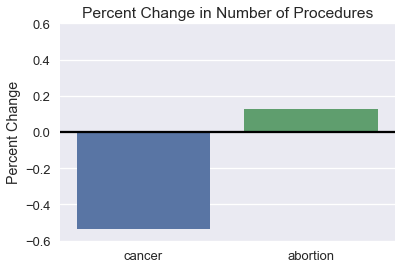
عند اختيار مقاسات المحاور نحاول التركيز على الجزء الذي يحتوي على عدد بيانات أكبر، خاصة عندما نعمل على بيانات المعروفة بأسم الذيل الطويل Long-tailed Data. لاحظ في الرسم البياني التالي الرسمه قبل (يسار) وبعد (يمين) التقريب في على الرسم الأخرى: 📝

الرسمه على اليمين تفيد أكثر في فهم البيانات. إذا احتاج الأمر، يمكننا رسم أكثر من رسمه بيانيه لأجزاء مختلفة من البيانات. لاحقاً في هذا الفصل، سنتحدث عن تحويل البيانات والذي سيساعدنا في رسم البيانات ذات الذيل الطويل.
مبادئ الحالات
تقدم لنا مبادئ الحالات الطرق والوسائل لإظهار التوزيع والعلاقة بين المجموعات الفرعية في بياناتنا.
يشرف مكتب إحصائيات العمال في الولايات المتحدة على إجراء استبيانات علمية لصحة اقتصاد الولايات المتحدة. يحتوي موقع المكتب على أداة لإنشاء التقارير باستخدام هذه البيانات التي استخدمناها لرسم متوسط الأجر الأسبوعي حسب الجنس.
أي المقارنات أسهل في هذا الرسم؟ هل هذه المقارنات هي الأهم؟
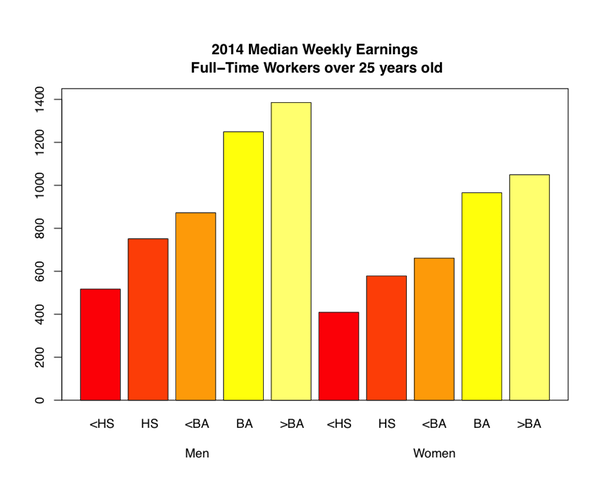
يبين لنا هذا الرسم لمحه بسيطه على أن الراتب الأجر الأسبوعي يزيد حسب الدرجة العلمية. ولكن، من الصعب تحديد الزيادة بالضبط بين كل درجه علميه وأخرى ويصعب أكثر التفريق بين أجور الذكور والإناث في نفس الدرجة العلمية. يمكننا التحقق من اتجاهات المشكلتين السابقتين باستخدام المخطط النقطي بدلاً من الشريطي:
لتحميل بيانات الأجور اضغط هنا.
cps = pd.read_csv("data/edInc2.csv")
ax = sns.pointplot(x="educ", y="income", hue="gender", data=cps)
ticks = ["<HS", "HS", "<BA", "BA", ">BA"]
ax.set_xticklabels(ticks)
ax.set_xlabel("Education")
ax.set_ylabel("Income")
ax.set_title("2014 Median Weekly Earnings\nFull-Time Workers over 25 years old");
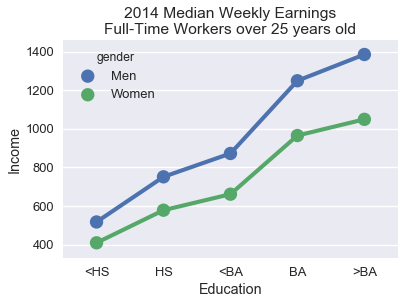
الخط الذي يربط بين النقاط يوضح تأثير الحصول على درجة البكالوريوس على الأجر الأسبوعي. وضع نقطتي الذكور والإناث فوق بعضهما يسهل علينا ملاحظة زيادة الفارق بينهما كلما زادت الدرجة العلمية.
للمساعدة في المقارنة بين المجموعتين الفرعيتين في بياناتنا، حاذي النقاط على المحور x أو y واختر ألوان أو أشكال مختلفة لكل منهما. الخطوط عادةً ما توضح اتجاه البيانات بشكل واضح أكثر من المخططات الشريطية وهي اختيار أفضل لنوعي البيانات النوعية والكمية.
مبادئ الإدراك
لدى إدراك البشر بعض الخصائص التي يجب ان ننتبه لها عند تصميم رسومنا البيانية. أول الخصائص في الإدراك البشري أننا ننتبه لبعض الألوان أكثر من أخرى، خاصة في درجات اللون الأخضر. أيضاً، نلاحظ أن الألوان الفاتحة أكبر حجماً من الألوان الغامقة. مثلاً، في الرسم البياني للأجور الأسبوعية، المخططات الشريطية الفاتحة تجذب انتباهنا أكثر من الغامقة:

عملياً، يجب أن تتأكد أن ألوان رسومك البيانية ذات إدراك موحد Perceptually Uniform. يعني ذلك، شدة الألوان لا تتغير بين كل شريط وآخر في الرسم. في البيانات الكمية، لدينا خياران: إذا كانت البيانات من تتصاعد من الأقل للأعلى فيجب عليك أن تشدد على القيم العليا، لذا تستخدم قالب ألوان متسلسلة Sequential Color Scheme والتي تعين لوناً فاتحاً للقيم العالية. إذا كانت كلا القيم العليا والدنيا تحتاج للتنويه عليها، استخدم قالب ألوان معكوس Diverging Color Scheme فيه يتم تعيين اللون الفاتح للقيم القريبة من المنتصف. 📝, 📝
تحتوي seaborn على الكثير من قوالب الألوان. يمكنك تصفحها في شرح المكتبة لمعرفة كيفية التغير بين كل قالب وآخر:
http://seaborn.pydata.org/tutorial/color_palettes.html
ثاني خصائص الإدراك البشري هي أننا دقيقين أكثر عندما نقارن بين الأطوال وأقل دقه عندما نقارن بين المساحات. الرسم البياني التالي للنواتج المحلية الإجمالية لبلدان أفريقيا:
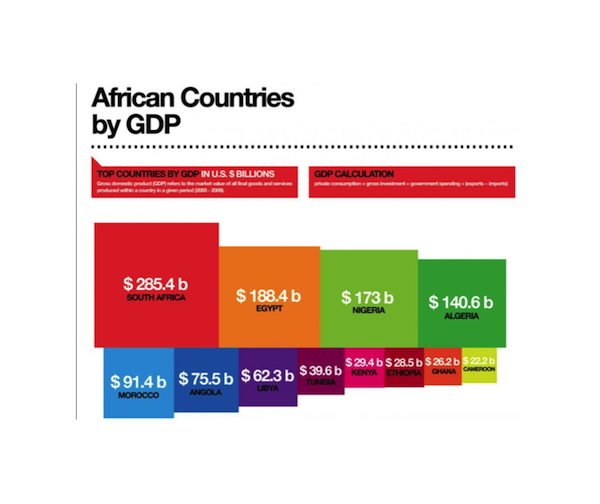
بِنَاءًا على الأرقام، جنوب أفريقيا لديها ضعف الناتج المحلي في بالجزائر ولكن ليس من السهل ملاحظة ذلك في الرسم البياني. بدلاً من ذلك، يمكننا استخدام المخطط النقطي للرسم:
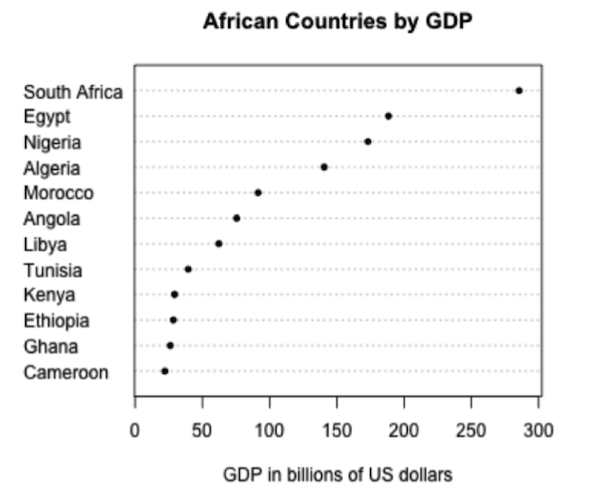
هذا أوضح بكثير لأنه سمح لنا المقارنة الطول بدلاً من المساحة. الدائرة الجزئية Pie Chart والرسوم ثلاثية الأبعاد Three-dimensional Charts يصعب ترجمتها بسبب نفس المشكلة؛ عملياً نحاول الابتعاد عن هذه الرسومات.
خاصية الإدراك البشري الثالثة والأخيرة هي أن العين تواجه صعوبات عند التنقل بين خطوط الأساس. في الرسم البياني التالي من النوع المساحي المُجَمع (المتكدس) Stacked Area Chart والذي يوضح انبعاثات ثاني أكسيد الكربون بمرور الوقت ومفصله حسب الدولة:
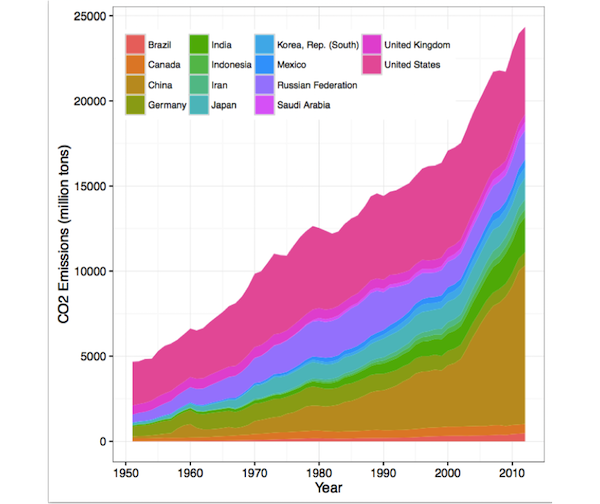
من الصعب معرفة ما إذا زادت أو نقصت الانبعاثات في المملكة المتحدة بسبب مشكلة هزهزة خط الأساس Jiggling Baseline: خط الأساس (الخط السفلي) للمساحة يهتز أعلى وأسفل. أيضا من الصعب المقارنة بين انبعاثات المملكة المتحدة والصين عندما يكون الطول متشابه (في عام 2000 مثلاً).
نفس المشكلة تظهر في المخطط الشريطي المُجَمع (المتكدس). في الرسم البياني التالي يصعب المقارنة عدد الذين أعمارهم بين 15-64 في المكسيك وألمانيا.
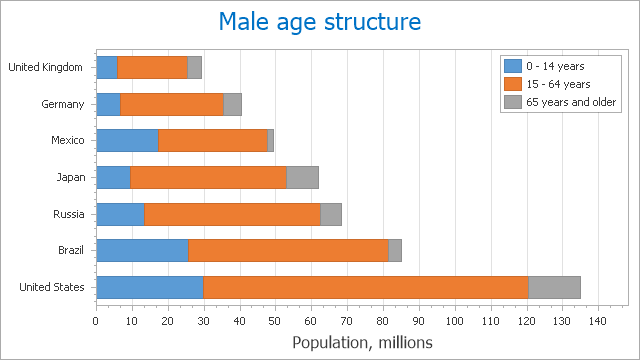
يمكننا تحسين رسوم البيانات من النوع المساحي والشريطي المُجمعه (متكدسة) عن طريق تحويلها إلى رسوم خطيه. الرسم البياني التالي لبيانات انبعاثات ثاني اكسيد الكربون بمرور الوقت كخطوط بدلاً من مساحات:
لتحميل بيانات انبعاثات ثاني أكسيد الكربون بين الدول اضغط هنا.
co2 = pd.read_csv("data/CAITcountryCO2.csv", skiprows = 2,
names = ["Country", "Year", "CO2"])
last_year = co2.Year.iloc[-1]
q = f"Country != 'World' and Country != 'European Union (15)' and Year == {last_year}"
top14_lasty = co2.query(q).sort_values('CO2', ascending=False).iloc[:14]
top14 = co2[co2.Country.isin(top14_lasty.Country) & (co2.Year >= 1950)]
from cycler import cycler
linestyles = (['-', '--', ':', '-.']*3)[:7]
colors = sns.color_palette('colorblind')[:4]
lines_c = cycler('linestyle', linestyles)
color_c = cycler('color', colors)
fig, ax = plt.subplots(figsize=(9, 9))
ax.set_prop_cycle(lines_c * color_c)
x, y ='Year', 'CO2'
for name, df in top14.groupby('Country'):
ax.semilogy(df[x], df[y], label=name)
ax.set_xlabel(x)
ax.set_ylabel(y + "Emissions [Million Tons]")
ax.legend(ncol=2, frameon=True);
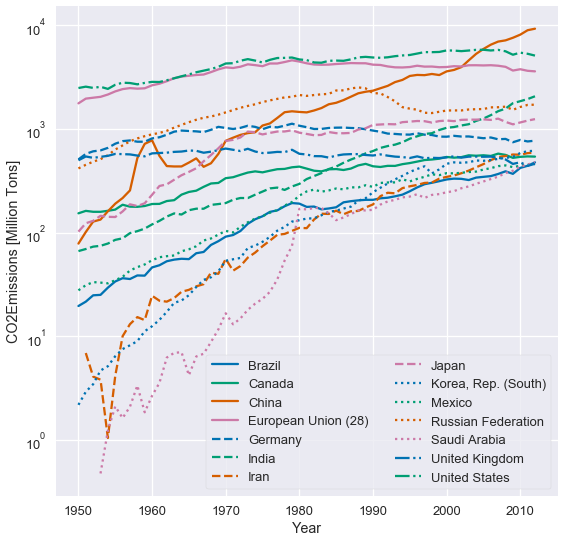
رسم البيانات على شكل خطوط لا يحدث بها اهتزازات في خط الأساس لكل خط لذا من السهل مقارنة الانبعاثات بين الدول. أيضا يمكننا أن نرى بوضوح أي الدول زادت فيها الانبعاثات.
مبادئ التحويل
تقدم لنا مبادئ التحويل طُرق مفيدة لتغير البيانات في الرسوم البيانية لإظهار اتجاهاتها بصورة واضحة. عادة ما نستخدم التحويل لإظهار الأنماط في البيانات المنحرفة Skewed Data أو العلاقات غير الخطية بين المتغيرات. 📝, 📝
الرسم البياني التالي يوضح توزيع أسعار التذاكر بين كل راكب في سفينة تايتانيك. كما ترى،الرسم منحرف باتجاه اليمين:
ti = sns.load_dataset('titanic')
sns.distplot(ti['fare'])
plt.title('Fares for Titanic Passengers')
plt.xlabel('Fare in USD')
plt.ylabel('Density');
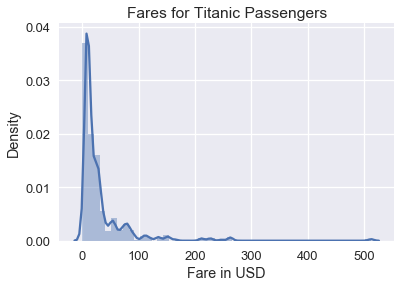
على الرغم أن الرسم البياني يوضح جميع أسعار التذاكر، من الصعب ملاحظة الأنماط فيها لأن البيانات مُتجمعة في الجهة اليسرى. لتحسين ذلك، يمكننا حساب اللوغاريتم الطبيعي Natural logarithm لأسعار التذاكر قبل رسمها:
sns.distplot(np.log(ti.loc[ti['fare'] > 0, 'fare']), bins=25)
plt.title('log(Fares) for Titanic Passengers')
plt.xlabel('log(Fare) in USD')
plt.ylabel('Density');
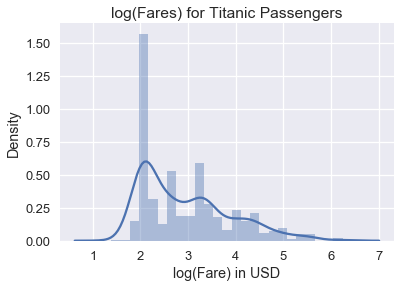
يمكننا ملاحظة في الرسم البياني أنه بعد حساب اللوغاريتمية أكثر القيم تكراراً (المنوال Mode) كان حوالي \(e^2 = \$7.40\) والأقل تكرارا كان \(e^{3.4} = \$30.00\). لماذا يفيدنا رسم اللوغاريتمية الطبيعية للبيانات عندما تكون مُنحرفة؟ اللوغاريتمية للأرقام العاليه عادة ما تكون قريبة من اللوغاريتمية للأرقام الصغيرة: 📝
| log(value) | value |
|---|---|
| 0 | 1 |
| 2.3 | 10 |
| 3.91 | 50 |
| 4.6 | 100 |
| 6.21 | 500 |
| 6.9 | 1000 |
يعني ذلك أن أخذ اللوغارتمية ستجلب تلك البيانات ذات الأرقام الكبيرة على الجانب الأيمن إلى الأرقام الصغيرة. يُسهل ذلك في توضيح أين تقع أغلب البيانات.
بالأصح، تعتبر اللوغارتم أداه مهمة في تحويل البيانات، تساعدنا أيضاً على ملاحظة العلاقات بين البيانات غير الخطية. في عام 1619، وثق يوهانس كيبلر البيانات التالية ليكتشف القانون الثالث في حركة الكواكب:
لتحميل بيانات يوهانس كيبلر عن حركة الكواكب اضغط هنا.
planets = pd.read_csv("data/planets.data", delim_whitespace=True,
comment="#", usecols=[0, 1, 2])
planets
| period | mean_dist | planet | |
|---|---|---|---|
| 87.77 | 0.389 | Mercury | 0 |
| 224.7 | 0.724 | Venus | 1 |
| 365.25 | 1 | Earth | 2 |
| 686.95 | 1.524 | Mars | 3 |
| 4332.62 | 5.2 | Jupiter | 4 |
| 10759.2 | 9.51 | Saturn | 5 |
إذا رسمنا متوسط المسافة حتى الشمس مقارنة بفترة الدوران، يمكننا ملاحظة أنه هناك علاقة لا تبدو خطيه:
sns.lmplot(x='mean_dist', y='period', data=planets, ci=False)
<seaborn.axisgrid.FacetGrid at 0x1a1f54aba8>
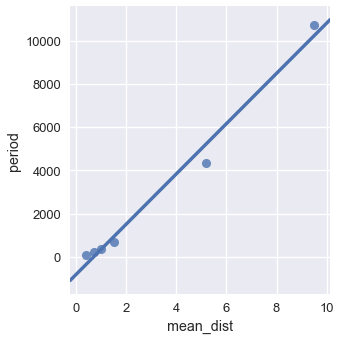
ولكن، إذا قمنا بحساب اللوغاريتمية لمتوسط المسافة والفترة، سنحصل على الرسم التالي:
sns.lmplot(x='mean_dist', y='period',
data=np.log(planets.iloc[:, [1, 2]]),
ci=False);
<seaborn.axisgrid.FacetGrid at 0x1a1f693da0>
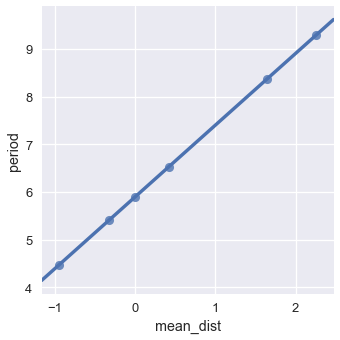
يمكن أن نرى علاقة خطية Linear بشكل شبه كامل هنا بين القيم اللوغاريتمية للمتوسط والفترة. ماذا يعني ذلك؟ بما أننا نعتقد أن هناك علاقة بين القيم اللوغارتمية، يمكننا استنتاج التالي:
\[\begin{aligned} \log(period) &= m \log(dist) + b \\ period &= e^{m \log(dist) + b} & \text{Taking the exponent of both sides} \\ period &= e^b dist^m \\ period &= C \cdot dist^m \end{aligned}\]قمنا بتبديل $e^b$ ب $C$ في الخطوة الأخيرة لتوضيح أن $e^b$ رقم ثابت. العملية الرياضية الجبرية السابقة تظهر أنه عندما تكون قيمتان لديهما علاقة متعددة الحدود Polynomial ، فإن لوغارتميتهما ذات علاقة خطيه. بالأصح، يمكننا إيجاد درجة متعددة حدود عن طريق إيجاد انحدار الخط Slope. في هذه الحالة، الانحدار قيمته 1.5 والذي يعطينا قانون كيبلر الثالث: $ period \propto dist^{1.5} $
بنفس طريقة الاستنتاج السابق يمكننا إظهار أن العلاقة بين $\log(y)$ و $x$ خطيه، القيمتين لديهما علاقة أسيه: $y = a^x$
بهذه الطرق، يمكننا استخدام اللوغارتمية لإظهار أنماط في البيانات ذات الذيل الطويل وعلاقات الغير خطية الشائعة بين القيم.
طرق أخرى في تحويل البيانات تشمل التحويلات متعدد الحدود وتحويل بوكس كوكس. 📝, 📝
مبادئ النصوص
من المهم إضافة أكبر قدر ممكن من النصوص التوضيحية لأي رسم بياني تنوي مشاركته بشكل واسع. مثلاً، الرسم البياني التالي تبدو البيانات فيه واضحة ولكن يقدم القليل من المعلومات التي تفيدنا في فهم ما تم رسمه:
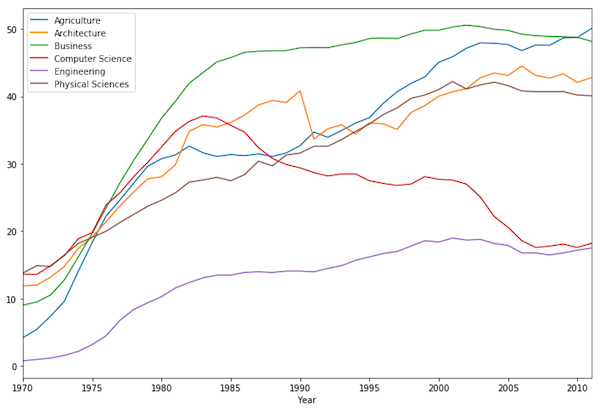
لتوضيح محتوى الرسم، أضفنا عنوان، عنوان فرعي، عناوين للمحاور ووحداتها، ومسميات للخطوط التي تم رسمها:
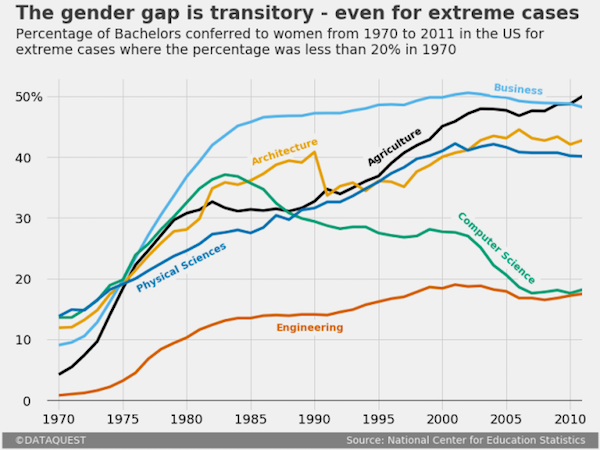
(التدوينة هنا توضح كيف تمت إضافة كل هذه التعديلات باستخدام matplotlib.)
بشكل عام، نضيف التالي إذا أردنا نصوصاً توضيحية في رسمنا البياني:
- عنوان الرسم.
- عناوين المحاور.
- إشارات للخطوط والعلامات ذات القيم المهمة.
- مسميات للنقاط المهمة والغير متوقعة.
- عنوان فرعي البيانات والمعلومات المهمة التي تقدمها.
مبادئ التبسيط
التبسيط يساعدنا في رسم البيانات بشكل واضح عندما تكون النقاط فيها كثيره. في الحقيقة سبق أن شاهدنا ذلك: المدرج التكراري هو نوع من التبسيط للرسم التخطيطي Rug Plots. الرسم التخطيطي التالي يوضح عمر كل شخص في تايتانيك:
ages = ti['age'].dropna()
sns.rugplot(ages, height=0.2)
<matplotlib.axes._subplots.AxesSubplot at 0x1a20c05b38>
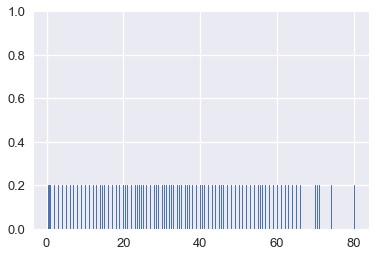
توجد الكثير من الخطوط التي تصعب علينا معرفة أين تقع أكثر البيانات. إضافة إلى انه بعض النقاط تتداخل في بعضها، ويصعب علينا ذلك معرفة كم نقطة تتجمع في 0. هذه المشكلة يطلق عليها فرط الرسم Overplotting ونحاول دائماً الابتعاد عن ذلك قدر الإمكان.
لإظهار توزيع البيانات، يمكننا التبديل بين إظهارها كمجموعة واحدة بشريط يمتد للأعلى عندما تكون هناك بيانات اضافيه في نفس النقطة. التبسيط يعني الخطوات لتبديل بعض النقاط بعلامات؛ نحاول عدم إظهار كل نقطه في البيانات لمحاولة الاتجاه العام للبيانات:
sns.distplot(ages, kde=False)
<matplotlib.axes._subplots.AxesSubplot at 0x1a23c384e0>
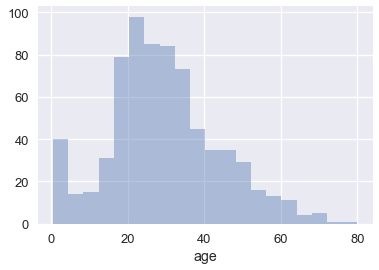
رأينا أَيْضًا أن seaborn سترسم خط منحني بشكل تلقائي في المدرج التكراري:
sns.distplot(ages)
<matplotlib.axes._subplots.AxesSubplot at 0x1a23d89780>
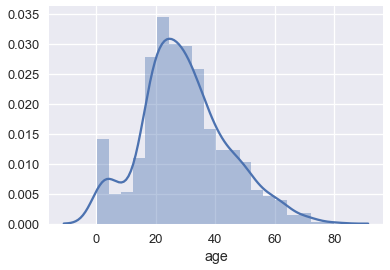
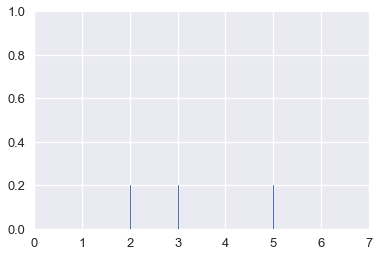
هذه طريقة أخرى من التبسيط تسمى تقدير كثافة النواة Kernel Density Estimation (KDE). بدلاً من تجميع النقاط معناً ورسم شريط، KDE تقوم برسم منحنى فوق كل نقطه وتجميعها كل منحنى وتحديد التقدير النهائي لتوزيع البيانات. لنأخذ الرسمة التخطيطية التالية لثلاث نقاط:
points = np.array([2, 3, 5])
sns.rugplot(points, height=0.2)
plt.xlim(0, 7);
لتطبيق تقدير كثافة النقاط نقوم برسم توزيع احتمالي طبيعي Normal Gaussian في كل نقطة:
from scipy.stats import norm
def gaussians(points, scale=True, sd=0.5):
x_vals = [np.linspace(point - 2, point + 2, 100) for point in points]
y_vals = [norm.pdf(xs, loc=point, scale=sd) for xs, point in zip(x_vals, points)]
if scale:
y_vals = [ys / len(points) for ys in y_vals]
return zip(x_vals, y_vals)
for xs, ys in gaussians(points, scale=False):
plt.plot(xs, ys, c=sns.color_palette()[0])
sns.rugplot(points, height=0.2)
plt.xlim(0, 7)
plt.ylim(0, 1);
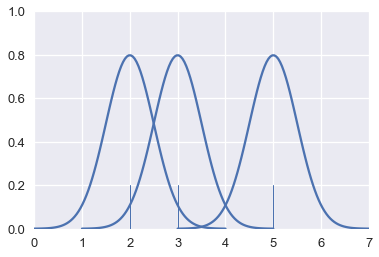
المساحة أسفل المنحنى الاحتمالي الطبيعي تساوي 1. بما أننا سنجمع أكثر من منحنى معاً، سنقوم بإعادة حساب مساحة كل منحنى حتى يكون مجموع كلا المنحنيات يساوي 1.
for xs, ys in gaussians(points):
plt.plot(xs, ys, c=sns.color_palette()[0])
sns.rugplot(points, height=0.2)
plt.xlim(0, 7)
plt.ylim(0, 1);
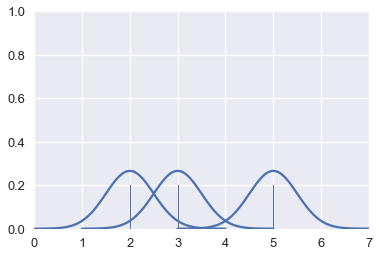
أَخِيرًا، نجمع كل المنحنيات معاً إيجاد المنحنى الأخير للتوزيع:
sns.rugplot(points, height=0.2)
sns.kdeplot(points, bw=0.5)
plt.xlim(0, 7)
plt.ylim(0, 1);
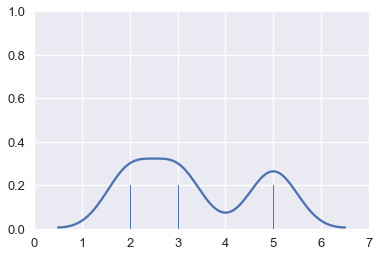
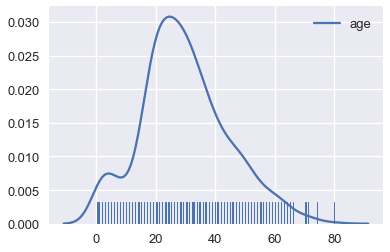
بإتباع نفس الطريقة، يمكننا استخدام KDE لتبسيط الكثير من النقاط:
# أظهار النقاط الاصلية قبل التبسيط
sns.rugplot(ages, height=0.1)
# اظهار تقدير التبسيط للتوزيع
sns.kdeplot(ages);
تفاصيل KDE
في المثال السابق، قمنا برسم منحنى بسيط فوق كل نقطة وجمعناهم معاً:
for xs, ys in gaussians(points):
plt.plot(xs, ys, c=sns.color_palette()[0])
sns.rugplot(points, height=0.2)
plt.xlim(0, 7)
plt.ylim(0, 1);
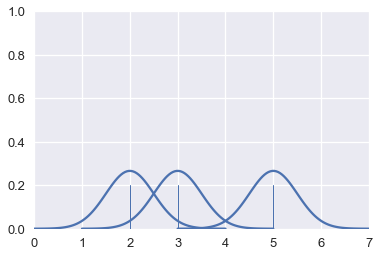
يمكننا التحكم بعرض المنحنيات. مثلاً، يمكننا تصغير حجمها. يسمى ذاك تقليل حجم نطاق Bandwidth تقدير الكثافة.
for xs, ys in gaussians(points, sd=0.3):
plt.plot(xs, ys, c=sns.color_palette()[0])
sns.rugplot(points, height=0.2)
plt.xlim(0, 7)
plt.ylim(0, 1);
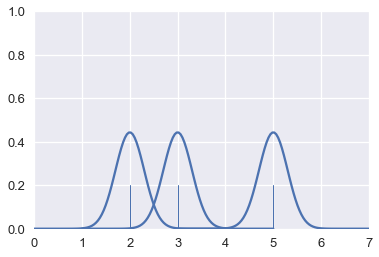
عندما نجمع المنحنيات ذات العرض الأقل معاً، نُنتِج تقدير نهائي أكثر تفصيلاً:
sns.rugplot(points, height=0.2)
sns.kdeplot(points, bw=0.2)
plt.xlim(0, 7)
plt.ylim(0, 1);
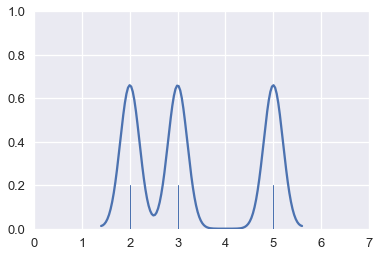
# رسم KDE لأعمار ركاب تايتانيك باستخدام نطاق اقل
sns.rugplot(ages, height=0.1)
sns.kdeplot(ages, bw=0.5);
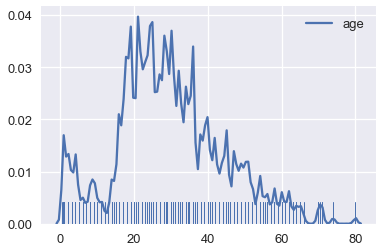
تماماً مثل التعديل في الأشرطة في المخطط الشريطي، عادة ما نقوم بالتعديل على النطاق حتى نرى أن الرسم البياني النهائي يظهر التوزيع دون تشتيت انتباه المتلقي بكثير من التفاصيل.
على الرغم من رسمنا لمنحنى في كل نقطة، يمكننا استخدام دوال أخرى للتقدير. يسمى ذلك تغير نواة Kernal تقدير كثافة النواة. سابقاً، استخدمنا نواة غاوسية Gaussian Kernal. الآن، سنستخدم نواة ثلاثية النقاط Triangular Kernal التي ترسم خطوط منحدره قبل وبعد كل نقطة.
sns.rugplot(points, height=0.2)
sns.kdeplot(points, kernel='tri', bw=0.3)
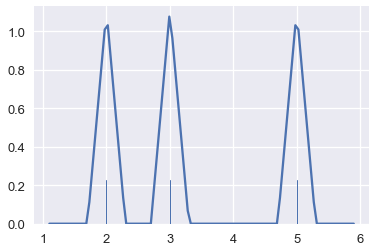
# رسم KDE لأعمار ركاب تايتانيك باستخدام نواه ثلاثية النطاق
sns.rugplot(ages, height=0.1)
sns.kdeplot(ages, kernel='tri');
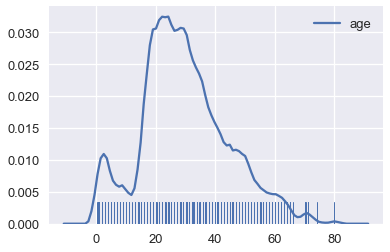
تفاصيل تبسيط مخططات التشتت
يمكننا تبسيط الرسوم ثنائية الأبعاد عندما نواجه مشكلة فرط الرسم.
المثال التالي تأتي بياناته من سباق أزهار الكرز، سباق سنوي ل 10 أميال في مدينة واشنطن العاصمة. كل متسابق سُجل عمره ووقت نهايته للسباق؛ قمنا برسم كل البيانات في مخطط التشتت التالي:
لتحميل بيانات سباق أزهار الكرز اضغط هنا.
runners = pd.read_csv('data/cherryBlossomMen.csv').dropna()
runners
| time | age | place | year | |
|---|---|---|---|---|
| 2819 | 28 | 1 | 1999 | 0 |
| 2821 | 24 | 2 | 1999 | 1 |
| 2823 | 27 | 3 | 1999 | 2 |
| … | … | … | … | … |
| 8840 | 56 | 7190 | 2012 | 70066 |
| 8850 | 35 | 7191 | 2012 | 70067 |
| 9059 | 48 | 7193 | 2012 | 70069 |
70045 rows × 4 columns
sns.lmplot(x='age', y='time', data=runners, fit_reg=False);
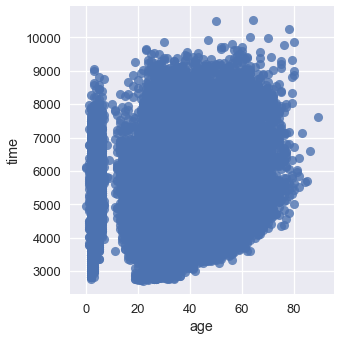
الكثير من النقاط متداخلة في بعضها البعض ويصعب بهذا الشكل تحديد اتجاه البيانات!
يمكننا تبسيط مخطط التشتت باستخدام KDE للرسوم ثنائية الأبعاد. عندما نطبقها على الرسمه، نقوم برسم منحنى ثلاثي الأبعاد على كل نقطه. بهذه الطريقة سيكون شكل المنحنى كالجبل ومتجه إلى الخارج:
# رسم ثلاث نقاط
two_d_points = pd.DataFrame({'x': [1, 3, 4], 'y': [4, 3, 1]})
sns.lmplot(x='x', y='y', data=two_d_points, fit_reg=False)
plt.xlim(-2, 7)
plt.ylim(-2, 7);
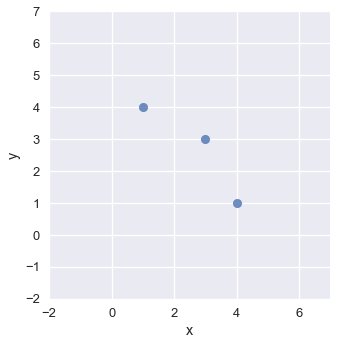
# رسم المنحنى لكل نقطه واستخدام مخطط المنسوب لإظهار كل واحد
sns.kdeplot(two_d_points['x'], two_d_points['y'], bw=0.4)
plt.xlim(-2, 7)
plt.ylim(-2, 7);
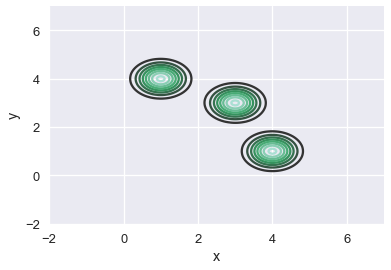
كما رأينا سابقاً، نعيد حساب المساحة لكل منحنى ونجمعها معاً حتى نصل لمخطط منسوبي Contour Plot نهائي لمخطط التشتت:
sns.kdeplot(two_d_points['x'], two_d_points['y'])
plt.xlim(-2, 7)
plt.ylim(-2, 7);
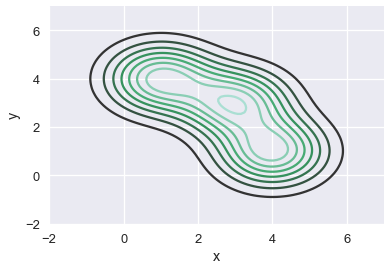
الرسمه النهائية توضح الميلان نحو الأسفل لكل الثلاث نقاط. بنفس الطريقة، يمكننا تطبيق KDE لتبسيط مخطط التشتت على بيانات الأعمار ووقت انتهاء المتسابقين للسباق:
sns.kdeplot(runners['age'], runners['time'])
plt.xlim(-10, 70)
plt.ylim(3000, 8000);
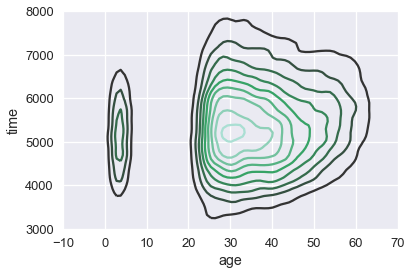
يمكن أن نلاحظ أن أكثر المتسابقين تتراوح أعمارهم بين 25 و 50 سنه، وأكثر المتسابقين استغرقوه 400 إلى 700 ثانيه (بين ساعة وساعتين) حتى ينهون السباق.
نلاحظ أَيْضًا وبشكل واضح أن هناك مجموعه من المتسابقين مشكوك بأمرها الذين بين 0 و 10 سنوات. ربما نحتاج إلى التحقق بشكل أكثر من بيانات الأعمار مما إذا كانت مسجله بشكل صحيح.
يمكن أَيْضًا أن نلاحظ بأن الوقت لإنهاء السباق يتجه للأعلى كلما زاد عمر المتسابق
فلسفة تصوير البيانات
للأسف، الكثير من الرسومات البيانية حول العالم لا تطبق مبادئنا في تصوير البيانات. هذه صفحة لرسومات بيانيه تظهر على الصفحة الأولى من بحث قوقل ل “good data visualization” تم أخذ الصورة في ربيع 2018. كم من الرسوم البيانية السيئة تلاحظ؟
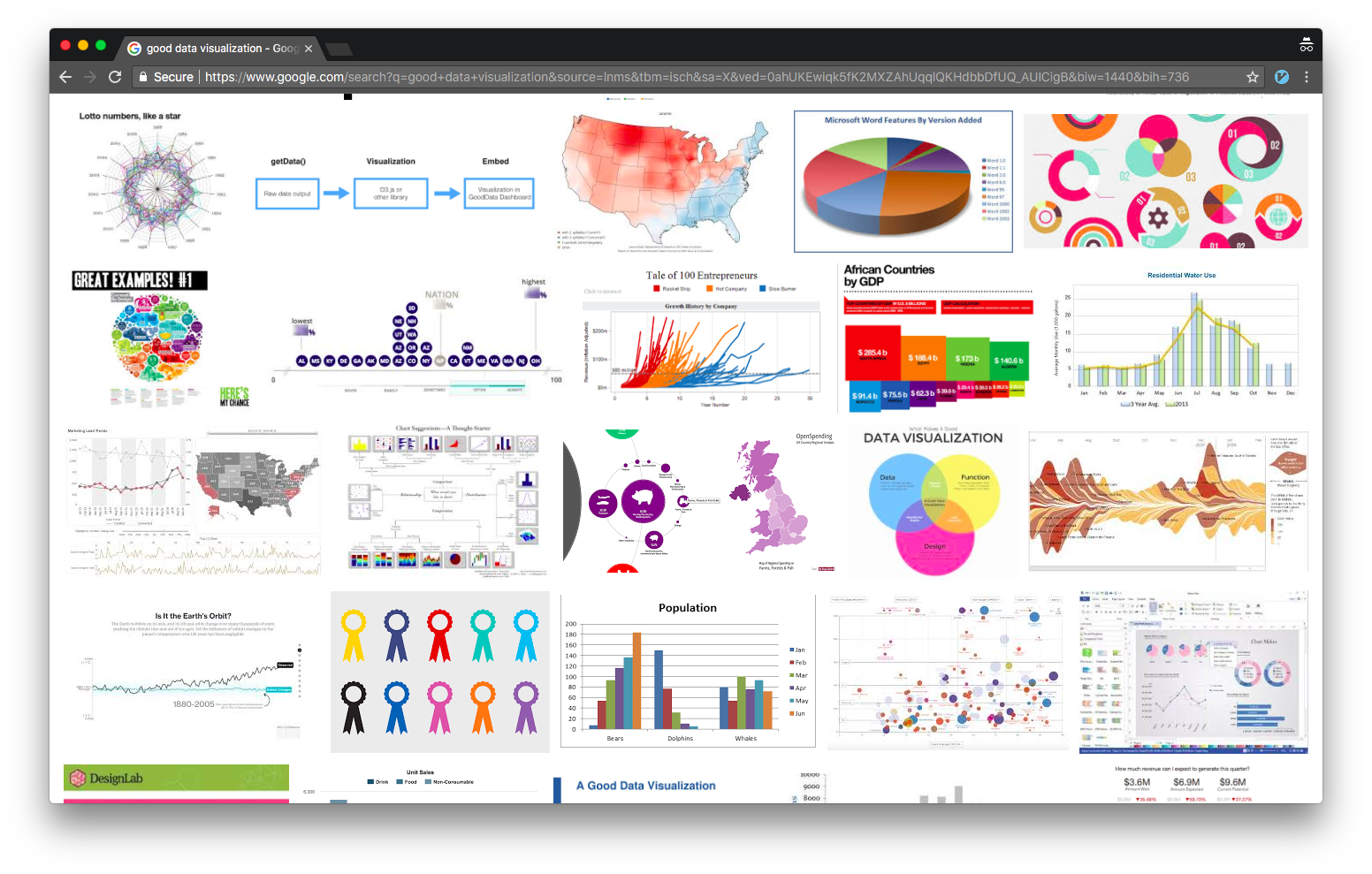
الرسم البياني الفعال يظهر البيانات بشكل أوضح. كل مبادئنا لرسم البيانات تهدف لجعل البيانات مفهومه للقارئ. تستخدم الرسوم البيانية أَحْيَانًا للتضليل وإظهار معلومات خاطئة. عندما يتم رسمها بشكل صحيح، الرسوم البيانية واحدة من أهم الأدوات لاكتشاف، توضيح والربط بين اتجاهات البيانات والشذوذ فيها.