مبادئ وتقنيات علم البيانات
الفصل السادس عشر: الضبط
فهرس الفصل:
مقدمة
يمكن لهندسة الخصائص أن تقدم لنا معلومات مهمة عن خطوات توليد البيانات في النموذج. ولكن، إضافة الخصائص إلى البيانات عادة ما يزيد من التباين في نموذجنا ويمكن لذاك أن يسيء من أداءه بشكل عام. بدلاً من إنشاء الخصائص بشكل عشوائي، يمكننا استخدام طريقة تسمى بـ الضبط Regularization للتقليل من التباين في نموذجنا مع الاستمرار بتقديم أكبر قدر من المعلومات عن البيانات.
فكرة الضبط
لنبدأ النقاش عن الضبط باستخدام المثال التالي لتوضيح أهميته.
بيانات سد المياه
البيانات التالية توضح كمية المياه باللتر التي تتدفق من سد المياه في اليوم و قيمة التغير في مستوى المياه في نفس اليوم بالمتر.
لتحميل البيانات water_large.csv اضغط هنا.
df = pd.read_csv('water_large.csv')
df
| water_flow | water_level_change | |
|---|---|---|
| 6.04E+10 | -15.936758 | 0 |
| 3.32E+10 | -29.152979 | 1 |
| 9.73E+11 | 36.189549 | 2 |
| … | … | … |
| 2.36E+11 | 7.08548 | 20 |
| 1.49E+12 | 46.282369 | 21 |
| 3.78E+11 | 14.612289 | 22 |
23 rows × 2 columns
عند رسم البيانات نلاحظ الاتجاه التصاعدي لتدفق المياه كلما كانت مستويات المياه إيجابية:
df.plot.scatter(0, 1, s=50);
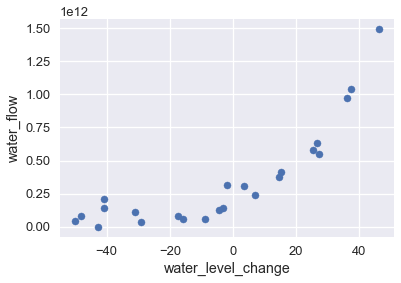
لنمذجة هذا النمط، يمكننا استخدام نموذج الانحدار الخطي للمربعات الصغرى Least Square Linear Regression. يظهر في الرسم البياني التالي البيانات وتوقعات النموذج:
df.plot.scatter(0, 1, s=50);
plot_curve(curves[0])
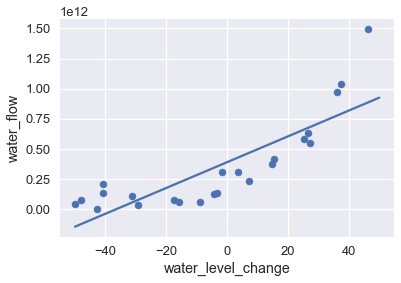
في الكود البرمجي السابق إستخدم الكاتب الدالة
plot_curveوالمصفوفةcurvesللمساعدة في الرسم، وعرفها كالتالي مع دالة مساعدة أخرىmake_curve:import matplotlib.pyplot as plt import numpy as np import pandas as pd from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from collections import namedtuple Curve = namedtuple('Curve', ['xs', 'ys']) def make_curve(clf, x_start=-50, x_end=50): xs = np.linspace(x_start, x_end, num=100) ys = clf.predict(xs.reshape(-1, 1)) return Curve(xs, ys) def plot_curve(curve, ax=plt, **kwargs): ax.plot(curve.xs, curve.ys, **kwargs) X = df.iloc[:, [0]].values y = df.iloc[:, 1].values degrees = [1, 2, 8, 12] clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', LinearRegression())]) .fit(X, y) for deg in degrees] curves = [make_curve(clf) for clf in clfs]
يظهر في الرسم البياني السابق أن هذا النموذج لا يغطي كامل النقاط في نمط هذه البيانات؛ والنموذج لدية انحياز عالي. كما فعلنا في السابق، يمكننا حل هذه المشكلة بإضافة خصائص متعددة الحدود للبيانات. نقوم بإضافة خصائص من الدرجة 2، 8 و 12؛ الرسوم البيانية التالية تظهر نتائج تدريب البيانات لكل نموذج:
plot_curves(curves)
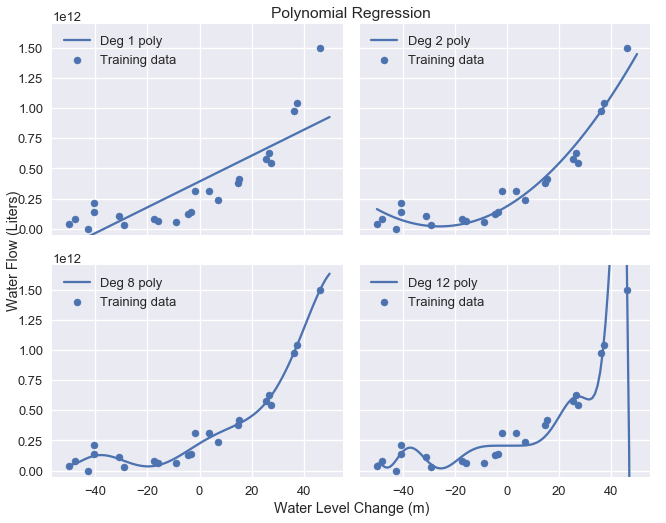
إستخدم الكاتب دالة
plot_curvesلنفس المصفوفة المستخدمة في المثال السابقcurvesللمساعدة في رسم النماذج، وعرفها كالتالي مع مزيد من الدوال المساعدة:def flatten(seq): return [item for subseq in seq for item in subseq] def plot_data(df=df, ax=plt, **kwargs): ax.scatter(df.iloc[:, 0], df.iloc[:, 1], s=50, **kwargs) def plot_curves(curves, cols=2): rows = int(np.ceil(len(curves) / cols)) fig, axes = plt.subplots(rows, cols, figsize=(10, 8), sharex=True, sharey=True) for ax, curve, deg in zip(flatten(axes), curves, degrees): plot_data(ax=ax, label='Training data') plot_curve(curve, ax=ax, label=f'Deg {deg} poly') ax.set_ylim(-5e10, 170e10) ax.legend() # إضافة الرسوم الكبيرة وإخفاء الإطارات fig.add_subplot(111, frameon=False) # إخفاء الحدود والعلامات والعناوين في الرسم plt.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off') plt.grid(False) plt.title('Polynomial Regression') plt.xlabel('Water Level Change (m)') plt.ylabel('Water Flow (Liters)') plt.tight_layout()
كما هو متوقع، متعددة الحدود من الدرجة الـ 12 طابقت بيانات التدريب بشكل مناسب ولكن يبدو أن النموذج مضبوط بنمط زائف على البيانات بسبب التشويش. يظهر ذلك نموذج آخر للمقايضة بين الانحياز والتباين؛ النموذج الخطي لدية انحياز عالي وتباين قليل بينما متعددة الحدود من الدرجة 12 لديها انحياز قليل وتبيان عالي.
التحقق من المعاملات
عند التحقق من معاملات نموذج متعددة الحدود من الدرجة الـ 12 يظهر لنا أن النموذج يقوم بالتوقع بناءًا على المعادلة التالية:
\[\begin{split} 207097470825 + 1.8x + 482.6x^2 + 601.5x^3 + 872.8x^4 + 150486.6x^5 \\ + 2156.7x^6 - 307.2x^7 - 4.6x^8 + 0.2x^9 + 0.003x^{10} - 0.00005x^{11} + 0x^{12} \end{split}\]فيها $ x $ هي قيمة تغير مستوى المياه في ذلك اليوم.
معاملات النموذج كبيرة جداً، خاصة لمتعددات الحدود ذات الدرجات العالية والتي تساهم بشكل عالي في تباين النموذج ( مثلاً $ x^5 $ و $ x^6 $ ).
معْلَمات المعاقبة
لنتذكر أن النموذج الخطي يقوم بالتوقعات بناءاً على التالي، $ \theta $ هي وزن النموذج و $ x $ هي متّجهة الخصائص:
\[f_\hat{\theta}(x) = \hat{\theta} \cdot x\]لضبط النموذج، نقوم بتقليل دالة التكلفة لمتوسط الخطأ التربيعي، فيها $ X $ تمثل مصفوفة البيانات و $ y $ هي النتائج التي اطلعت عليها:
\[\begin{split} \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2\\ \end{aligned} \end{split}\]لتقليل التكلفة في المعادلة السابقة، نقوم بضبط $ \hat{\theta} $ حتى نصل لأفضل قيم للأوزان Weights أياً كان حجمها. لكن، وجدنا أن كلما كان الوزن عالي وبخصائص أكثر تعقيداً ينتج لنا تباين عالي للنموذج. على العكس، إذا كان بإمكاننا التعديل في دالة التكلفة لمعاقبة الأوزان العالية، سيكون النموذج الناتج ذو تباين قليل. نستخدم الضبط للقيام بذلك.
الضبط L2: انحدار Ridge
في هذا الجزء سنتعرف على طريقة الضبط $ L_2 $، طريقة لمعاقبة الأوزان الكبيرة في دوال التكلفة للتقليل من تباين النموذج. راجعنا بشكل مبسط الانحدار الخطي، ثم تعرفنا على الضبط كأداة للتعديل في دالة التكلفة.
لتطبيق الانحدار الخطي للمربعات الصغرى، نستخدم النموذج:
\[f_\hat{\theta}(x) = \hat{\theta} \cdot x\]نقوم بضبط النموذج عن طريق التقليل دالة تكلفة متوسط الخطأ التربيعي:
\[\begin{split} \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}^n(y_i - f_\hat{\theta} (X_i))^2\\ \end{aligned} \end{split}\]في المعادلة السابقة، $ X $ تمثل مصفوفة البيانات $ n \times p $، و $ x $ تمثل سطر من أسطر $ X $، و $ y $ تمثل النتائج التي أطلع عليها، و $ \hat{\theta} $ هي وزن النموذج.
التعريف
لإضافة الضبط $ L_2 $ إلى النموذج، نقوم بتعديل دالة التكلفة السابقة:
\[\begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2 + \lambda \sum_{j = 1}^{p} \hat{\theta_j}^2 \end{aligned}\]نلاحظ أن دالة التكلفة مشابهة للسابقة مع إضافة الضبط $ L_2 $ في المعادلة $ \lambda \sum_{j = 1}^{p} \hat{\theta_j}^2 $. المجموع ( $ \sum $ ) في هذه المعادلة يقوم بجمع تربيع كل وزن في النموذج $ \hat{\theta_1}, \hat{\theta_2}, \ldots, \hat{\theta_p} $. يظهر لنا في المعادلة أيضاً رمز جديد لمتغير رقمي في النموذج $ \lambda $ والذي يتم تعديله لتحديد قيمة عقوبة الضبط Regularization Penalty.
معادلة الضبط الذي أضفناها تسبب زيادة في التكلفة إذا كانت القيم في $ \hat{\theta} $ بعيدة عن صفر. مع إضافة الضبط، الوزن للنموذج المثالي يقلل من الخسارة ومعاقبة الضبط بدلاً من الخسارة فقط. بما أن نتائج أوزان النموذج عادة ما تكون قليلة، فسيكون النموذج ذو تبيان قليل وانحياز عالي.
استخدام الضبط $ L_2 $ مع نموذج خطي ودالة التكلفة لمتوسط الخطأ التربيعي يطلق عليه انحدار Ridge. 📝
متغيرات الضبط
يتحكم متغير الضبط $ \lambda $ بعقوبة الضبط. عندما تكون $ \lambda $ قليلة ينتج قيمة عقاب قليل، إذا كانت $ \lambda = 0 $ تكون قيمة معاقبة الضبط أيضاً $ 0 $ وبالتالي لم يتم ضبط دالة التكلفة.
عندما تكون $ \lambda $ عالية ينتج لنا قيمة عقاب عاليه وبالتالي يكون النموذج بسيط. الزيادة في $ \lambda $ تقلل من التباين وتزيد من الانحياز في النموذج. نستخدم التحقق المتقاطع لاختيار قيمة $ \lambda $ التي تقلل من خطأ التحقق.
ملاحظة عن الضبط في مكتبة scikit-learn:
توفر مكتبة scikit-learn نموذج الانحدار ومضاف إليها بشكل تلقائي الضبط. مثلاً، لتطبيق انحدار Ridge يمكنك استخدام النموذج الخطي sklearn.linear_model.Ridge. لاحظ أن جميع النماذج في مكتبة scikit-learn تطلق على متغير الضبط alpha بدلاً من $ \lambda $.
توفر مكتبة scikit-learn بشكل بسيط ومناسب نماذج مضبوطة تقوم بتطبيق التحقق المتقاطع لاختيار قيمة مناسبة لـ $ \lambda $. مثلاً، sklearn.linear_model.RidgeCV يسمح للمستخدم إدخال قيم متغيرات الضبط وبشكل أوتوماتيكي تقوم بتطبيق التحقق المتقاطع لاختيار أفضل قيمة للمتغير والذي يحصل على أقل خطأ في بيانات التحقق.
استبعاد مصطلح الانحياز
لاحظ أن رمز الانحياز $ \theta_0 $ لم يتم ضمة لعملية الجمع في معادلة الضبط. لا نقوم بمعاقبة الانحياز لأن الزيادة في انحياز النموذج لا تؤدي للزيادة في التباين؛ ببساطة يقوم الانحياز بتغير جميع التوقعات إلى قيم ثابتة.
تسوية البيانات
لاحظ أن معادلة الضبط $ \lambda \sum_{j = 1}^{p} \hat{\theta_j}^2 $ تعاقب كل $ \hat{\theta_j} $ بشكل متكافئ. ولكن، تأثير كل قيمة من $ \hat{\theta_j} $ يختلف بناءاً على البيانات نفسها. لنأخذ مثلاً هذه الجزء من بيانات تدفق المياه بعد إضافة متغيرات متعددة الحدود من الدرجة الثامنة:
pd.DataFrame(clfs[2].named_steps['poly'].transform(X[:5]),
columns=[f'deg_{n}_feat' for n in range(8)])
| deg_7_feat | deg_6_feat | … | deg_1_feat | deg_0_feat | |
|---|---|---|---|---|---|
| 4161020472.12 | -261095791.08 | … | 253.98 | -15.94 | 0 |
| 521751305227.70 | -17897014961.65 | … | 849.9 | -29.15 | 1 |
| 2942153527269.12 | 81298431147.09 | … | 1309.68 | 36.19 | 2 |
| 3904147586408.71 | 104132296999.30 | … | 1405.66 | 37.49 | 3 |
| 28456763821657.70 | -592123531634.12 | … | 2309.65 | -48.06 | 4 |
5 rows × 8 columns
نلاحظ أن متعددة الحدود من الدرجة السابعة حصلت على قيم أعلى بكثير عن متعددة الحدود من الدرجة الأولى. يعني ذلك أن الوزن العالي في نموذج متعددة الحدود من الدرجة السابعة أثر على التوقعات أكثر من الوزن عالي لنموذج متعددة الحدود من الدرجة الأولى. إذا قمنا بتطبيق الضبط على هذه البيانات مباشرة، ستقوم معاقبة الضبط بتقليل الوزن للنموذج بشكل غير مناسب للخصائص في الدرجات الصغرى. بشكل عملي، ينتج عن ذلك تباين عالي للنموذج حتى بعد تطبيق الضبط لأن الخصائص ذات التأثير الأكبر على التوقعات لن تتأثر.
لحل ذلك، نقوم بـ التسوية Normalization جميع الأعمدة عن طريق طرح المتوسط منها وتغير القيم فيها إلى شكل مدرج Scale بين -1 و 1. في مكتبة scikit-learn أغلب نماذج الانحدار تسمح بتطبيق التسوية باستخدام المتغير normalize=True للقيام بتسوية البيانات قبل الضبط. 📝 📝
طريقة أخرى مشابهة للتسوية هي التوحيد Standardization لأعمدة البيانات عن طريق طرح المتوسط وتقسيمه على الانحراف المعياري لكل عمود.
استخدام انحدار Ridge
استخدمنا سابقاً خصائص متعددة الحدود لضبط متعددات الحدود من الدرجة 2، 8 و 12 لبيانات تدفق المياه. البيانات الأساسية ونتائج توقعات النموذج كالتالي:
df
| water_flow | water_level_change | |
|---|---|---|
| 60422330445.52 | -15.94 | 0 |
| 33214896575.60 | -29.15 | 1 |
| 972706380901.06 | 36.19 | 2 |
| … | … | … |
| 236352046523.78 | 7.09 | 20 |
| 1494256381086.73 | 46.28 | 21 |
| 378146284247.97 | 14.61 | 22 |
23 rows × 2 columns
plot_curves(curves)
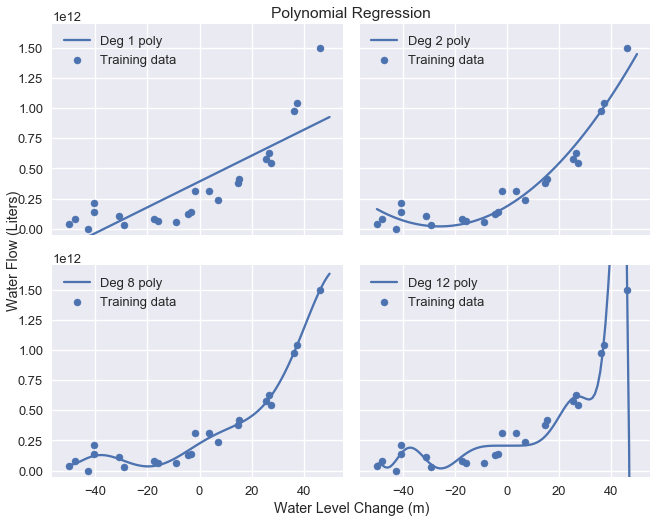
لتطبيق انحدار Ridge، نقوم أولاً باستخراج مصفوفة البيانات و متّجهة النتائج من البيانات:
X = df.iloc[:, [0]].values
y = df.iloc[:, 1].values
print('X: ')
print(X)
print()
print('y: ')
print(y)
X:
[[-15.94]
[-29.15]
[ 36.19]
...
[ 7.09]
[ 46.28]
[ 14.61]]
y:
[6.04e+10 3.32e+10 9.73e+11 ... 2.36e+11 1.49e+12 3.78e+11]
ثم نقوم بتحويل القيم في X إلى متعددة الحدود من الدرجة 12:
from sklearn.preprocessing import PolynomialFeatures
# نريد تحديد include_bias=False
# لأن مصنفات مكتبة sklearns
# تقوم بشكل تلقائي بإضافة قيم الانحياز
X_poly_8 = PolynomialFeatures(degree=8, include_bias=False).fit_transform(X)
print('First two rows of transformed X:')
print(X_poly_8[0:2])
First two rows of transformed X:
[[-1.59e+01 2.54e+02 -4.05e+03 6.45e+04 -1.03e+06 1.64e+07 -2.61e+08
4.16e+09]
[-2.92e+01 8.50e+02 -2.48e+04 7.22e+05 -2.11e+07 6.14e+08 -1.79e+10
5.22e+11]]
نقوم بتحديد قيم alpha التي ستختارها مكتبة scikit-learn باستخدام التحقق المتقاطع، ثم نستخدم نموذج RidgeCV لضبط البيانات بعد التحويل:
from sklearn.linear_model import RidgeCV
alphas = [0.01, 0.1, 1.0, 10.0]
# تذكر ان تحدد normalize=True
# ليتم تسوية البيانات
clf = RidgeCV(alphas=alphas, normalize=True).fit(X_poly_8, y)
# إظهار قيمة Alpha
clf.alpha_
0.1
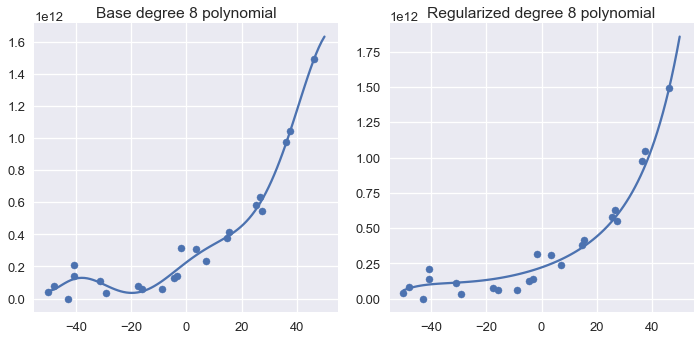
أخيراً، نقوم برسم نتائج التوقعات لنموذج متعددة الحدود من الدرجة الثامنة بجانب النموذج من الدرجة الثامنة الذي تم ضبطه:
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plot_data()
plot_curve(curves[2])
plt.title('Base degree 8 polynomial')
plt.subplot(122)
plot_data()
plot_curve(ridge_curves[2])
plt.title('Regularized degree 8 polynomial')
plt.tight_layout()
إستخدم الكاتب نفس الطريقة السابقة لرسم انحدار Ridge، عن طريق إنشاء مصفوفة أسماها
ridge_curvesوعرفها كالتالي:from sklearn.linear_model import Ridge ridge_clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', Ridge(alpha=0.1, normalize=True))]) .fit(X, y) for deg in degrees] ridge_curves = [make_curve(clf) for clf in ridge_clfs]
نلاحظ أن متعددة الحدود التي تم ضبطها منحناها أكثر سلاسة وتمر على أغلب نقاط البيانات.
بمقارنة المعامِلات للنموذج الذي تم ضبطه والذي لم يتم ضبطه نلاحظ أن انحدار Ridge يفضل وضح وزن للنموذج على متعددات الحدود ذو الدرجات الدنيا:
base = coef_table(clfs[2]).rename(columns={'Coefficient Value': 'Base'})
ridge = coef_table(ridge_clfs[2]).rename(columns={'Coefficient Value': 'Regularized'})
pd.options.display.max_rows = 20
display(base.join(ridge))
pd.options.display.max_rows = 7
| Regularized | Base | |
|---|---|---|
| degree | ||
| 221063525725.23 | 225782472111.94 | 0 |
| 6846139065.96 | 13115217770.78 | 1 |
| 146158037.96 | -144725749.98 | 2 |
| 1930090.04 | -10355082.91 | 3 |
| 38240.62 | 567935.23 | 4 |
| 564.21 | 9805.14 | 5 |
| 7.25 | -249.64 | 6 |
| 0.18 | -2.09 | 7 |
| 0.00 | 0.03 | 8 |
استخدم الكاتب دالتين
coef_tableوcoefsتقومان بإنشاء المُعامِلات على شكل جدول في DataFrame، وتعريفها كالتالي:def coefs(clf): reg = clf.named_steps['reg'] return np.append(reg.intercept_, reg.coef_) def coef_table(clf): vals = coefs(clf) return (pd.DataFrame({'Coefficient Value': vals}) .rename_axis('degree'))
إعادة تطبيق نفس العملية على متعددة الحدود من الدرجة 12 يظهر نتائج مماثلة:
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plot_data()
plot_curve(curves[3])
plt.title('Base degree 12 polynomial')
plt.ylim(-5e10, 170e10)
plt.subplot(122)
plot_data()
plot_curve(ridge_curves[3])
plt.title('Regularized degree 12 polynomial')
plt.ylim(-5e10, 170e10)
plt.tight_layout()
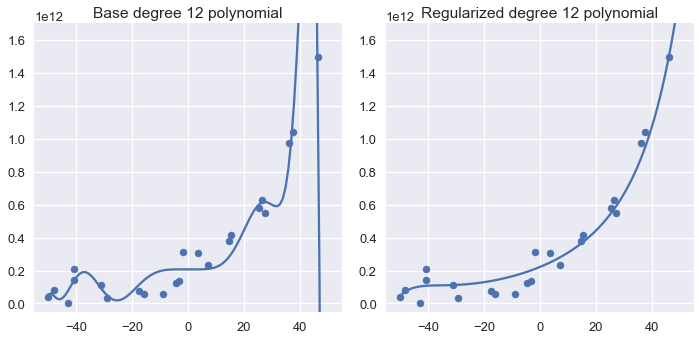
نحصل على نموذج أكثر بساطة كلما قمنا في الزيادة في متغير الضبط. الرسم البياني التالي يوضح تأثير الزيادة في قيمة الضبط من 0.001 حتى 100.0:
alphas = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
alpha_clfs = [Pipeline([
('poly', PolynomialFeatures(degree=12, include_bias=False)),
('reg', Ridge(alpha=alpha, normalize=True))]
).fit(X, y) for alpha in alphas]
alpha_curves = [make_curve(clf) for clf in alpha_clfs]
labels = [f'$\\lambda = {alpha}$' for alpha in alphas]
plot_curves(alpha_curves, cols=3, labels=labels)
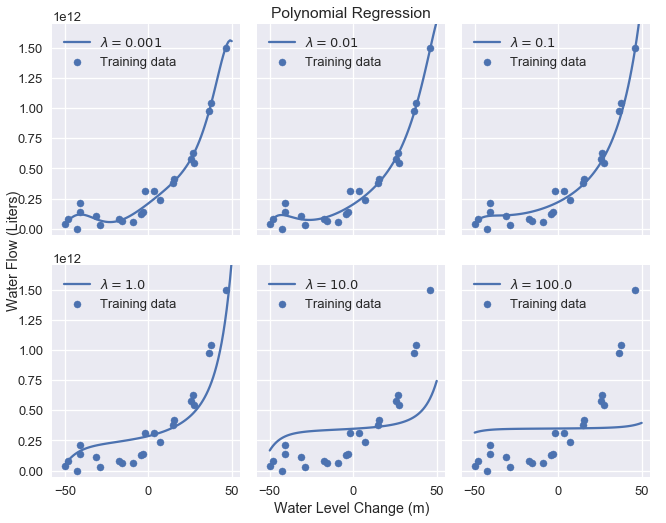
إستخدمت الدالة
plot_curvesللمساعدة على رسم المنحنيات، وتعريفها كالتالي:def plot_curves(curves, cols=2, labels=None): if labels is None: labels = [f'Deg {deg} poly' for deg in degrees] rows = int(np.ceil(len(curves) / cols)) fig, axes = plt.subplots(rows, cols, figsize=(10, 8), sharex=True, sharey=True) for ax, curve, label in zip(flatten(axes), curves, labels): plot_data(ax=ax, label='Training data') plot_curve(curve, ax=ax, label=label) ax.set_ylim(-5e10, 170e10) ax.legend() # إضافة الرسوم الكبيرة وإخفاء الإطارات fig.add_subplot(111, frameon=False) # إخفاء الحدود والعلامات والعناوين في الرسم plt.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off') plt.grid(False) plt.title('Polynomial Regression') plt.xlabel('Water Level Change (m)') plt.ylabel('Water Flow (Liters)') plt.tight_layout()
كما نرى، الزيادة في متغير الضبط تزيد من انحياز النموذج. إذا كان متغير الضبط عالي جداً، يصبح النموذج نموذجاً ثابتاً لأن أي قيمة لوزن النموذج غير صفر ينتج عنها عقاب عالي.
ملخص انحدار Ridge
استخدام ضبط $ L_2 $ يسمح لنا بضبط انحياز وتباين النموذج عن طريق عقاب أوزان النموذج العالية. ضبط $ L_2 $ للانحدار الخطي للمربعات الصغرى يعرف أيضاً باسم انحدار Ridge. استخدام الضبط يضيف متغير إضافي للنموذج يرمز له $ \lambda $ والذي نقوم بضبطه باستخدام التحقق المتقاطع.
الضبط L1: انحدار Lasso
في هذا الجزء سنتعرف على طريقة الضبط $ L_1 $، طريقة أخرى من طرق الضبط تفيدنا في اختيار الخصائص.
سنبدأ بمراجعة بسيطة للضبط $ L_2 $ للانحدار الخطي. استخدمنا النموذج:
\[f_\hat{\theta}(x) = \hat{\theta} \cdot x\]قمنا بضبط النموذج عن طريق تقليل دالة التكلفة لمتوسط الخطأ التربيعي وأضفنا إليها الضبط:
\[\begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2 + \lambda \sum_{j = 1}^{p} \hat{\theta_j}^2 \end{aligned}\]في المعادلة السابقة، $ X $ تمثل مصفوفة البيانات $ n \times p $، و $ x $ تمثل سطر من أسطر $ X $، و $ y $ تمثل النتائج التي أطلع عليها، و $ \hat{\theta} $ هي وزن النموذج، و $ \lambda $ تمثل قيمة متغير الضبط.
تعريف الضبط
لإضافة الضبط $ L_1 $ إلى النموذج، نقوم بتعديل دالة التكلفة السابقة إلى:
\[\begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2 + \lambda \sum_{j = 1}^{p} |\hat{\theta_j}| \end{aligned}\]لاحظ أن الفرق بين المعادلتين فقط في جزئية الضبط. الضبط $ L_1 $ يعاقب مجموع الأوزان المطلقة بدلاً من مجموع التربيع.
استخدام الضبط $ L_2 $ مع نموذج خطي ودالة التكلفة لمتوسط الخطأ التربيعي يطلق عليه انحدار Lasso. (Lasso هي اختصار ل Least Absolute Shrinkage and Selection Operator معامل الانكماش والاختيار المطلق الأقل.) 📝
المقارنة بين انحدار Ridge و Lasso
لتطبيق انحدار Lasso، سنستخدم النموذج LassoCV من مكتبة scikit-learn، وهي نسخة من نموذج Lasso التي تطبق التحقق المتقاطع لاختيار متغيرات الضبط. في الأسفل، نستعرض بيانات تدفق المياه من السد:
df
| water_flow | water_level_change | |
|---|---|---|
| 60422330445.52 | -15.94 | 0 |
| 33214896575.60 | -29.15 | 1 |
| 972706380901.06 | 36.19 | 2 |
| … | … | … |
| 236352046523.78 | 7.09 | 20 |
| 1494256381086.73 | 46.28 | 21 |
| 378146284247.97 | 14.61 | 22 |
23 rows × 2 columns
بما أن الخطوات في كلا الطريقتين متطابقة، سنستعرض النتائج لجميع النماذج معاً مع متعددة الحدود من الدرجة 12.:
fig = plt.figure(figsize=(10, 4))
plt.subplot(131)
plot_data()
plot_curve(curves[3])
plt.title('Base')
plt.ylim(-5e10, 170e10)
plt.subplot(132)
plot_data()
plot_curve(ridge_curves[3])
plt.title('Ridge Regression')
plt.ylim(-5e10, 170e10)
plt.subplot(133)
plot_data()
plot_curve(lasso_curves[3])
plt.title('Lasso Regression')
plt.ylim(-5e10, 170e10)
plt.tight_layout()
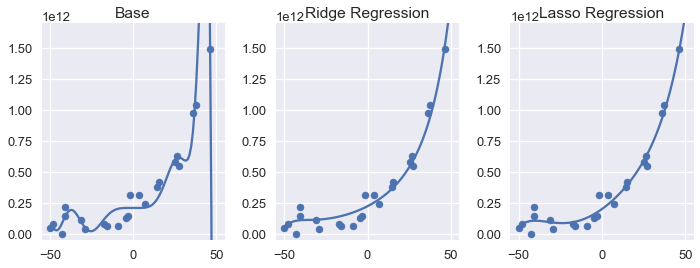
إستخدم الكاتب نفس الطريقة السابقة لرسم انحدار Lasso، عن طريق إنشاء مصفوفة أسماها
lasso_curvesوعرفها كالتالي:from sklearn.linear_model import LassoCV lasso_clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', LassoCV(normalize=True, precompute=True, tol=0.001))]) .fit(X, y) for deg in degrees] lasso_curves = [make_curve(clf) for clf in lasso_clfs]
نلاحظ ان كلا النموذجين المضبوطة لديها تباين قليل مقارنة مع متعددة الحدود من الدرجة 12. نلاحظ أن استخدام الضبط $ L_2 $ أو $ L_1 $ ينتج لنا نتائج قريبة جداً أن تكون متطابقة. لكن، عند مقارنة المُعاملات لنموذجي انحدار Ridge و Lasso، يظهر لنا أهم الفروقات بين النوعين من الضبط: نموذج انحدار Lasso حدد بعض من أوزان النموذج إلى القيمة صفر:
ridge = coef_table(ridge_clfs[3]).rename(columns={'Coefficient Value': 'Ridge'})
lasso = coef_table(lasso_clfs[3]).rename(columns={'Coefficient Value': 'Lasso'})
pd.options.display.max_rows = 20
pd.set_option('display.float_format', '{:.10f}'.format)
display(ridge.join(lasso))
pd.options.display.max_rows = 7
pd.set_option('display.float_format', '{:.2f}'.format)
| Lasso | Ridge | |
|---|---|---|
| degree | ||
| 198212062407 | 221303288116 | 0 |
| 9655088668 | 6953405308 | 1 |
| 198852674.2 | 142621063.9 | 2 |
| 0 | 1893283.057 | 3 |
| 34434.34589 | 38202.15203 | 4 |
| 975.6965959 | 484.4262914 | 5 |
| 0 | 8.152512652 | 6 |
| 0.0887942172 | 0.1197232472 | 7 |
| 0 | 0.0012506185 | 8 |
| 0 | 0.0000289599 | 9 |
| 0 | -0.0000000004 | 10 |
| 0 | 0.0000000069 | 11 |
| 0 | -0.0000000001 | 12 |
عند العودة للنتائج في الجدول، نلاحظ أن انحدار Ridge كانت نتائجه غير صفريه للأوزان في جميع خصائص متعددة الحدود. بينما انحدار Lasso، كانت لدية نتائج تساوي صفر في سبعة من الخصائص.
بمعنى آخر، أن نموذج انحدار Lasso تجاهل بشكل كامل الكثير من الخصائص عند القيام بالتوقعات. ولكن، الرسم البياني السابق أظهر أن نموذج انحدار Lasso قام بتوقعات مطابقة بشكل كبير لنموذج انحدار Ridge.
اختيار الخصائص مع انحدار Lasso
عندما يقوم انحدار Lasso بتطبيق اختيار الخصائص Feature Selection، يتجاهل أجزاء من الخصائص الأصلية عند ضبط الخصائص بالنموذج. هذه الطريقة مفيدة عندما نعمل على بيانات عالية الأبعاد بخصائص كثيره. نموذج يستخدم القليل من الخصائص للقيام بالتوقعات سيعمل بشكل أسرع من نموذج آخر يحتاج الكثير من عمليات الحساب. بما أن الخصائص غير المرغوب فيها تزيد من تباين النموذج دون التقليل من الانحياز، يمكننا أحياناً زيادة دقة النماذج عن طريق استخدام انحدار Lasso ليقوم باختيار جزء من الخصائص ليستخدمها.
Ridge × Lasso عملياً
إذا كان هدفنا فقط الوصول إلى أعلى دقة في التوقع، يمكننا تجربة كلا النوعين من الضبط مع التحقق المتقاطع والاختيار بينهما.
أحياناً نفضل نوع من الضبط عن الآخر لأنها يطابق بشكل كثير المجال الذي نعمل عليه. مثلاً، إذا كنا نعرف أن ظاهره ما والتي نحاول أن نبني لها نموذج تنتج من العديد من العوامل الصغيرة، فربما نفضل استخدام انحدار Ridge لأنه لن يتجاهل أحد هذه العوامل الصغيرة. من ناحية أخرى، بعض النتائج تأتي جزء الخصائص شديدة التأثير. نفضل استخدام انحدار Lasso في تلك الحالات لأنه يتجاهل الخصائص غير المرغوب فيها.
ملخص انحدار Lasso
استخدام الضبط $ L_1 $، كما في الضبط $ L_2 $، يساعدنا على ضبط انحياز وتباين النموذج عن طريق معاقبة الأوزان العالية في النموذج. الضبط $ L_1 $ لانحدار خطي ودالة التكلفة لمتوسط الخطأ التربيعي يطلق عليه بالمصطلح الشائع انحدار Lasso. يمكن أن ستخدم انحدار Lasso في اختيار الخصائص بما أنه يتجاهل الخصائص غير المهمة.