مبادئ وتقنيات علم البيانات
الفصل الثاني عشر: الاحتماليات والتعميم
فهرس الفصل:
مقدمة
تعرفنا على خطوات إنشاء نماذج باستخدام البيانات:
- اختيار النموذج.
- اختيار دالة الخسارة.
- ضبط النموذج عن طريق تقليل الخسارة.
حتى الآن، تعرفنا على النموذج الثابت، عدد مختلف من دوال الخسارة، والنزول الاشتقاقي كوسيلة عامه للتقليل من الخسارة. إتباع هذه الخطوات عادةً ما يكوّن لنا نموذج يقوم بتوقعات صحيحه على البيانات التي تدرب عليها.
للأسف، فائدة النموذج الذي يأتي بشكل جيد على بيانات التدريب عند تطبيقه على بيانات مختلفة محدود وقليل. نهتم بإمكانية النموذج على التعميم. نحتاج أن يكون نموذجنا قادر على التوقع بشكل صحيح بشكل عام، ليس فقط على بيانات التدريب. هذه المشكلة قد تبدو صعبة، قد تتساءل كيف يمكننا الإجابة وتوقع نتائج بيانات لم نرها بعد؟
هنا نستعين بالاستنتاجات في الإحصاء. سنتعرف أولاً على بعض الأدوات الرياضية: العينات العشوائية، التوقع والتباين. باستخدام هذه الأدوات، سنتمكن من إيجاد توقعات مستقبليه لأداء النموذج على بياناتنا، وحتى تلك التي لم يتدرب النموذج عليها!
المتغيرات العشوائية
تحتوي جميع الظواهر في العالم الحقيقي على القليل من العشوائية، مما يجعل تكوين وجمع البيانات عشوائياً بشكل طبيعي. لأننا نضبط نماذجنا على هذه البيانات، فإن النماذج أيضاً تحتوي على بعض العشوائية. للتعبير عن هذه العشوائية بشكل رياضي، نستخدم المتغيرات العشوائية.
المتغير العشوائي Random Variable هو متغير جبري يمثل قيمه رقمية / عدديه تم تحديديها بواسطة الاحتمالات. في هذا الكتاب، سنستخدم دائماً الحروف الكبيرة مثل $ X $ و $ Y $ لتمثيل متغير عشوائي. على الرغم أن المتغيرات العشوائية يمكن تمثيلها بعدة أشكال كقيم منفصله ( مثلاً عدد الذكور في عينة من 10 أشخاص) أو كقيم متسلسلة (مثلاً متوسط درجة الحرارة في لوس أنجلوس)، في هذا الكتاب، سنستخدم المتغيرات العشوائية المنفصلة. 📝 📝
يجب علينا دائماً تحديد ما يمثله المتغير العشوائي. مثلاً، قد نكتب أن المتغير العشوائي $ X $ يمثل عدد مرات ظهور صورة في 10 مرات من رمي العملة المعدنية. تعريف المتغير العشوائي يحدد القيم التي بداخله. في المثال السابق، $ X $ ستأخذ فقط القيم من $ 0 $ إلى $ 10 $.
يجب علينا أيضاً تحديد احتمالية ظهور أي من القيم المحتملة في المتغير العشوائي. مثلاً، احتمالية أن $ X = 0 $ يتم كتابتها كالتالي $ P(X = 0) = (0.5)^{10} $ كذلك وبنفس الطريقة يمكننا حساب احتمالية أن $ X $ هي أي قيمه من بين القيم التالية $ \{ 0, 1, \ldots, 10 \} $.
دالة كتلة الاحتمال
دالة كتلة الاحتمال Probability Mass Function (PMF) أو توزيع Distribution المتغير العشوائي $ X $ تقدم لنا احتمالية أن $ X $ هي أحد القيم المحتملة. إذا جعلنا $ \mathbb{X} $ ترمز لمصفوفة القيم التي يمكن أن تمثلها $ X $ و $ x $ قيمه معينة من القيم في $ \mathbb{X} $، فإن دالة كتلة الاحتمال ل $ X $ يجب أن توفي الشروط التالية: 📝
\[1) \sum_{x \in \mathbb{X}} P(X = x) = 1\] \[2) \text{ For all } x \in \mathbb{X}, 0 \leq P(X = x) \leq 1\]الشرط الأول يقول إن مجموع الاحتماليات للقيم فيه $ X $ يساوي $ 1 $.
الشرط الثاني يقول إن احتمالية كل قيمه من القيم في $ X $ يجب أن تكون بين $ 0 $ و $ 1 $.
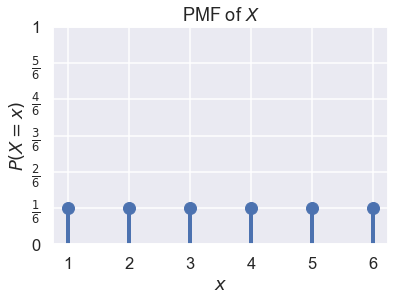
لنفترض أن $ X $ تمثل نتيجة رمي حجر النرد. نعلم أن $ X \in \{1, 2, 3, 4, 5, 6\} $ و أن $ P(X = 1) = P(X = 2) = \ldots = P(X = 6) = \frac{1}{6} $. يمكننا رسم نتيجة PMF ل $ X $ كالتالي:
التوزيعات المشتركة
بشكل تلقائي، تمتد فكرة التوزيع PMF للمتغير العشوائي إلى التوزيع المشترك للعديد من المتغيرات العشوائية. بشكل أوضح، التوزيع المشترك Joint Distribution لمتغيران عشوائيان أو أكثر ينتج عنه احتماليه أن هذه المتغيرات العشوائية تأخذ نفس مصفوفة القيم. 📝
مثلاً، المتغير العشوائي $ X $ يمثل عدد مرات ظهور صوره عند رمي العملة المعدنية 10 مرات، و $ Y $ تمثل عدد مرات ظهور كتابه عند رمي العملة المعدنية 10 مرات. يمكننا ملاحظة أن:
\[P(X=0, Y=10) = P(X=10, Y=0) = (0.5)^{10}\]بينما $ P(X=6, Y=6) = 0 $ لأنه من المستحيل أن نحصل على 6 صور و 6 كتابات في 10 رميات.
التوزيع الهامشي
أحياناً، نبدأ بتوزيع مشترك لمتغيران عشوائيان $ X $ و $ Y $ ولكن نريد البحث عن توزيع $ X $ فقط. يطلق على ذلك التوزيع الهامشي Marginal Distribution. لإيجاد احتمالية $ X $ لقيمه معينة، يجب علينا الأخذ بالاعتبار جميع القيم المحتملة ل $ Y $ والتي قد تأتي مع $ X $ وجمع كل هذه الاحتماليات المشتركة: 📝
\[\begin{aligned} \sum_{y \in \mathbb{Y}} P(X=x, Y=y) &= P(X=x) \end{aligned}\]يمكننا إثبات ذلك على النحو التالي:
\[\begin{split} \begin{aligned} \sum_{y \in \mathbb{Y}} P(X=x, Y=y) &= \sum_{y \in \mathbb{Y}} P(X=x) \times P(Y=y \; \vert \; X=x)\\ &= P(X=x) \times \sum_{y \in \mathbb{Y}} P(Y=y \; \vert \; X=x)\\ &= P(X=x) \times 1 \\ &= P(X=x) \end{aligned} \end{split}\]في السطر الأخير من الإثبات، تعاملنا مع $ Y \; \vert \; X = x$ كقيم عشوائية مع PMF غير معروفة. ذلك يهمنا لأننا استخدمنا الخاصية الأولى التي تقول إن مجموع الاحتماليات ل PMF يجب أن يساوي 1، يعني ذلك أن $ \sum_{y\in \mathbb{Y}} P(Y = y \; \vert \; X = x) = 1 $.
المتغيرات العشوائية المستقلة
كما في الأحداث، المتغيران العشوائيين قد يكونا مستقلان أو غير مستقلان. أي متغيرين عشوائيين يكونان مستقلان فقط اذا كانت معرفة نتيجة إحداهما لا تأثر على احتمالية أي نتيجة للمتغير الآخر.
مثلاً، عند رمي العملة المعدنية عشر مرات لنجعل $ X $ تكون عدد مرات ظهور الصورة و $ Y $ عدد مرات ظهور الكتابة. بشكل واضح، $ X $ و $ Y $ غير مستقلان كون معرفتنا أن $ X = 0 $ تعني أن $ Y = 10 $.
يمكننا بدلاً من ذلك إجراء جولتين لرمي العملة المعدنية عشر مرات. إذا كانت $ X $ هي عدد مرات ظهور صوره في الجولة الأولى و $ Y $ هي عدد مرات ظهور صوره في الجولة الثانية، فإن $ X $ و $ Y $ مستقلان لأن النتائج للجولة الأولى من رمي العملة المعدنية لا تأثر على النتائج من رمي العملة المعدنية في الجولة الثانية.
مثال على الأعمار
لنفترض أن لدينا البيانات البسيطة التالية لأربع أشخاص:
| Age | Name | |
|---|---|---|
| 50 | Carol | 0 |
| 52 | Bob | 1 |
| 51 | John | 2 |
| 50 | Dave | 3 |
لنفترض اننا أخذنا شخصين كعينه من هذه البيانات ووضعنا اشخاص بدلاً منهم. اذا كان المتغير العشوائي $ Z $ يمثل الفرق في الأعمار بين الشخص الأول والثاني في العينة، فما هو توزيع المتغير العشوائي PMF ل $ Z $?
لحل هذه المشكله، نقوم من جديد بتعريف متغيران عشوائيان. نقوم بتعريف $ X $ كعمر الشخص الأول و $ Y $ كعمر للشخص الثاني. فأن $ Z = X - Y $. ثم نوجد توزيع الإحتمالات المشتركة ل $ X $ و $ Y $، والتي تعني الإحتماليه لكل متغير أن يحصل عليها بنفس الوقت. في هذه الحاله، نلاحظ أن $ X $ و $ Y $ مستقلان وموزعين بالتساوي؛ كلا المتغيران العشوائيان يمثلان احتمالات عشوائية مستقله للإختيار من بين البيانات، وعملية الإختيار الأولى لا تأثر على الثانيه. مثلاً، إحتمالية أن $ X = 51 $ و $ Y = 50 $ هي $ P(X = 51, Y = 50) = \frac{1}{4} \cdot \frac{2}{4} = \frac{2}{16} $. بنفس الطريقه، نحصل على التالي:
| $Y=52$ | $Y=51$ | $Y=50$ | |
|---|---|---|---|
| $\frac{2}{16}$ | $\frac{2}{16}$ | $\frac{4}{16}$ | $X=50$ |
| $\frac{1}{16}$ | $\frac{1}{16}$ | $\frac{2}{16}$ | $X=51$ |
| $\frac{1}{16}$ | $\frac{1}{16}$ | $\frac{2}{16}$ | $X=52$ |
دعنا الآن نأخذ بعين الاعتبار لو أخذنا شخصان من هذه البيانات دون توفير بدائل لهم. كما في السابق، نعرف $ X $ كالعمر للشخص الأول و $ Y $ العمر للشخص الثاني، و $ Z = X - Y $. ولكن، الآن $ X $ و $ Y $ ليست مستقلة؛ مثلاً، إذا عرفنا أن $ X = 51 $، فإن $ Y \neq 51 $. ونجد التوزيع المشترك ل $ X $ و $ Y $ كالتالي:
| $Y=52$ | $Y=51$ | $Y=50$ | |
|---|---|---|---|
| $\frac{2}{12}$ | $\frac{2}{12}$ | $\frac{2}{12}$ | $X=50$ |
| $\frac{1}{12}$ | $ 0 $ | $\frac{2}{12}$ | $X=51$ |
| $ 0 $ | $\frac{1}{12}$ | $\frac{2}{12}$ | $X=52$ |
يمكننا إيجاد التوزيع الهامشي ل $ Y $ من الجدول:
\[\begin{split} \begin{aligned} P(Y = 50) &= P(Y = 50, X = 50) + P(Y = 50, X = 51) + P(Y = 50, X = 52) \\ &= \frac{2}{12} + \frac{2}{12} + \frac{2}{12} \\ &= \frac{1}{2} \\ P(Y = 51) &= \frac{2}{12} + 0 + \frac{1}{12} = \frac{1}{4} \\ P(Y = 52) &= \frac{2}{12} + \frac{1}{12} + 0 = \frac{1}{4} \end{aligned} \end{split}\]لاحظ أننا قمنا بجمع كل عمود من التوزيع المشترك في الجدول العلوي. يمكن للشخص حساب نتائج الجمع لكل عمود وكتابتها على الهامش أسفل الجدول؛ هذه كانت بداية فكرة المصطلح التوزيع الهامشي.
يجب أن تلاحظ أيضاً أن $ X $ و $ Y $ ليست مستقلة عندما نأخذ عينات دون توفير بدائل. مثلاً، إذا كانت $ X = 52 $ فإن $ Y \neq 52 $. مع ذلك، لا يزال التوزيع الهامشي بين $ X $ و $ Y $ نفسه.
ملخص المتغيرات العشوائية
في هذا الجزء، تعرفنا على المتغيرات العشوائية، متغيرات رياضية تأخذ قيم بناءًا على عملية عشوائية. هذه النتائج يجب أن تعرف بشكل كامل ودقيق، كل نتيجة يجب أن تحتوي على احتماليه معرفة بشكل واضح للحالات. المتغير العشوائي مفيد جداً في كثير من الحالات، بما فيها عملية جمع البيانات.
التوقع والتباين
على الرغم أن المتغير العشوائي يتم وصفحه بشكل كامل بواسطة دالة PMF الخاصة به، عادةً ما نستخدم التوقع و التباين لوصف متوسط وتوزيع المتغير على المدى الطويل. هذان المتغيران لديهما خصائص رياضية مميزة والتي لديها أهمية خاصة لعلم البيانات. مثلاً، يمكننا إظهار أن التوقع صحيح على المدى البعيد عن طريق إظهار نتيجة التوقع مساويه لقيمه معْلَمة المجتمع الإحصائي. سنبدأ بتعريف التوقع والتباين، والتعرف على أهم خصائصهم الرياضية، والانتهاء بتطبيق بسيط على التوقع. 📝
التوقع
بالعادة، يهمنا متوسط القيمة العشوائية على المدى البعيد لأنها تعطينا نظره عن توزيع البيانات. نطلق على المتوسط على المدى البعيد القيمة المتوقعة Expected Value، أو التوقع Expectation للقيمة العشوائية. التوقع القيمة العشوائية $ X $ هو:
\[\mathbb{E}[X] = \sum_{x\in \mathbb{X}} x \cdot P(X = x)\]مثلاً، إذا كانت $ X $ تمثل رمي حجر النرد مرة واحدة:
\[\begin{split} \begin{aligned} \mathbb{E}[X] &= 1 \cdot P(X = 1) + 2 \cdot P(X = 2) + \ldots + 6 \cdot P(X = 6) \\ &= 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + \ldots + 6 \cdot \frac{1}{6} \\ &= 3.5 \end{aligned} \end{split}\]لاحظ أن القيمة المتوقعة ل $ X $ لا يجب أن تكون القيمة المحتملة لها. على الرغم أن $ \mathbb{E}[X] = 3.5 $، ولكن $ X $ لا يمكنها أن تكون القيمة $ 3.5 $
القيمة 3.5 ليست موجودة في حجر النرد، القيمة المتوقعة هي من 1 حتى 6.
مثال: لنعود للبيانات في الجزء السابق.
| Age | Name | |
|---|---|---|
| 50 | Carol | 0 |
| 52 | Bob | 1 |
| 51 | John | 2 |
| 50 | Dave | 3 |
نختار شخصاً واحداً من هذه البيانات بشكل محايد وعشوائي. لتكون $ Y $ هي القيمة العشوائية التي تمثل عمر هذا الشخص. إذاً:
\[\begin{split} \begin{aligned} \mathbb{E}[Y] &= 50 \cdot P(Y = 50) + 51 \cdot P(Y = 51) + 52 \cdot P(Y = 52) \\ &= 50 \cdot \frac{2}{4} + 51 \cdot \frac{1}{4} + 52 \cdot \frac{1}{4} \\ &= 50.75 \end{aligned} \end{split}\]مثال: لنفرض أننا سنأخذ عينتين من البيانات مع استبدالهم. إذا كانت القيمة العشوائية $ Z $ تمثل الفرق في العمر بين الشخص الأول والثاني في هذه العينة، فما هي $ \mathbb{E}[Z] $؟
كما في الجزء السابق، عرفنا $ X $ على أنا عمر الشخص الأول، و $ Y $ هي عمر الشخص الثاني، ف $ Z = X - Y $. من التوزيع المشترك ل $ X $ و $ Y $ الذي أعطي في الجزء السابق، يمكننا إيجاد دالة كتلة الاحتمال ل $ Z $، مثلاً:
\[P(Z = 1) = P(X = 51, Y = 50) + P(X = 52, Y = 51) = \frac{3}{16}\]فإن:
\[\begin{split} \begin{aligned} \mathbb{E}[Z] &= (-2) \cdot P(Z = -2) + (-1) \cdot P(Z = -1) + \ldots + (2) \cdot P(Z = 2) \\ &= (-2) \cdot \frac{2}{16} + (-1) \cdot \frac{3}{16}+ \ldots + (2) \cdot \frac{2}{16} \\ &= 0 \end{aligned} \end{split}\]بما أن $ \mathbb{E}[Z] = 0 $، فأننا نتوقع على المدى البعيد أن الفرق في الأعمار في عينه ذات الحجم 2 يساوي 0.
خطية التوقع
عند التعامل مع مجموعات خطية للمتغيرات العشوائية كما رأينا في الأمثلة السابقة، يمكننا عادةً استخدام خطية التوقع Linearity of Expectations بدلاً من الحساب يدوياً للتوزيع المشترك. 📝
خطية التوقع يمكن وصفها كالتالي:
\[\begin{split} \begin{aligned} \mathbb{E}[X + Y] &= \mathbb{E}[X] + \mathbb{E}[Y] \\ \end{aligned} \end{split}\]ومن ذلك الوصف يمكننا قول التالي:
\[\begin{split} \begin{aligned} \mathbb{E}[cX] &= c\mathbb{E}[X] \\ \end{aligned} \end{split}\]وفيها $ X $ و $ Y $ هي متغيرات عشوائية، و $ c $ رقم ثابت.
يمكننا القول، التوقع لمجموع متغيرين عشوائيين هو مجموع التوقع للمتغيرات.
في المثال السابق، رأينا أن $ Z = X - Y $. فإن:
\[\mathbb{E}[Z] = \mathbb{E}[X - Y] = \mathbb{E}[X] - \mathbb{E}[Y]\]الآن يمكننا حساب $ \mathbb{E}[X] $ و $ \mathbb{E}[Y] $ بشكل منفصل عن بعضهما. لأن $ \mathbb{E}[X] = \mathbb{E}[Y] = 50.75 $ فإن $ \mathbb{E}[Z] = 50.75 - 50.75 = 0 $.
يمكن حساب خطية التوقع حتى لو كانت $ X $ و $ Y $ غير مستقلان! كمثال، لنأخذ شخصين من نفس البيانات في الجزء السابق دون توفير بديل لهم. كما في السابق، عرفنا $ X $ أنها عمر الشخص الأول و $ Y $ هي عمر الشخص الثاني، و $ Z = X - Y $. بشكل واضح، $ X $ و $ Y $ غير مستقلان، معرفة أن $ X = 52 $، تعني أن $ Y \neq 52 $.
من خلال التوزيع المشترك ل $ X $ و $ Y $ الذي سبق أن أعطي في الجزء السابق، يمكننا إيجاد $ \mathbb{E}[Z] $:
\[\begin{split} \begin{aligned} \mathbb{E}[Z] &= (-2) \cdot P(Z = -2) + (-1) \cdot P(Z = -1) + \ldots + (2) \cdot P(Z = 2) \\ &= (-2) \cdot \frac{2}{12} + (-1) \cdot \frac{3}{12}+ \ldots + (2) \cdot \frac{2}{12} \\ &= 0 \end{aligned} \end{split}\]طريقة أسهل لإيجاد التوقع هي استخدام خطية التوقع. حتى ولو كانت $ X $ و $ Y $ مستقلان، فإن $ \mathbb{E}[Z] = \mathbb{E}[X - Y] = \mathbb{E}[X] - \mathbb{E}[Y] $. لنتذكر من الجزء السابق أن $ X $ و $ Y $ لديهما نفس قيمة PMF حتى عندما قمنا بأخذ عينات دون توفير بدائل، والذي يعني أن $ \mathbb{E}[X] = \mathbb{E}[Y] = 50.75 $. وبالتالي، فكما في المثال الأول، $ \mathbb{E}[Z] = 0 $.
لاحظ أن خطية التوقع فقط تنطبق على القيم الخطية من المتغيرات العشوائية. مثلاً، $ \mathbb{E}[XY] = \mathbb{E}[X]\mathbb{E}[Y] $ ليست خطيه ل $ X $ و $ Y $. في هذه الحالة، $ \mathbb{E}[XY] = \mathbb{E}[X]\mathbb{E}[Y] $ هي صحيحه بشكل عام فقط للمتغيرات العشوائية المستقلة.
التباين
التباين لمتغير عشوائي هي تعبير رقمي لتوزيع المتغير. مثلاً، للمتغير العشوائي $ X $:
\[\begin{split} \begin{aligned} Var(X) &= \mathbb{E}[(X - \mathbb{E}[X])^2] \\ \end{aligned} \end{split}\]المعادلة السابقة تقول إن التباين ل $ X $ هو تربيع متوسط المسافة للقيمة المتوقعة ل $ X $.
مع بعض العمليات الرياضية التي لم نكتبها للاختصار، يمكننا أن نكتب المعادلة بالشكل التالي:
\[\begin{split} \begin{aligned} Var(X) &= \mathbb{E}[X^2] - \mathbb{E}[X]^2 \\ \end{aligned} \end{split}\]لنأخذ المتغيرين العشوائيين $ X $ و $ Y $ ولديهما التوزيعات الاحتمالية التالية:
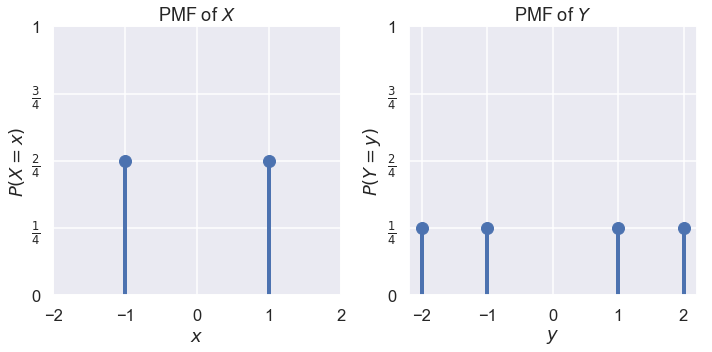
تأخذ $ X $ القيم $ -1 $ و $ 1 $ مع احتمالية $ \frac{1}{2} $ لهما. بينما تأخذ $ Y $ القيم $ -2 $، $ -1 $، $ 1 $ و $ 2 $ مع احتمالية $ \frac{1}{4} $ لكل قيمه. وجدنا أن $ \mathbb{E}[X] = \mathbb{E}[Y] = 0 $. لأن توزيع $ Y $ أعلى من $ X $، فأننا نتوقع أن $ Var(Y) $ أكبر من $ Var(X) $.
\[\begin{split} \begin{aligned} Var(X) &= \mathbb{E}[X^2] - \mathbb{E}[X]^2 \\ &= \mathbb{E}[X^2] - 0^2 \\ &= \mathbb{E}[X^2] \\ &= (-1)^2 P(X = -1) + (1)^2 P(X = 1) \\ &= 1 \cdot 0.5 + 1 \cdot 0.5 \\ &= 1 \\\\ Var(Y) &= \mathbb{E}[Y^2] - \mathbb{E}[Y]^2 \\ &= \mathbb{E}[Y^2] - 0^2 \\ &= \mathbb{E}[Y^2] \\ &= (-2)^2 P(Y = -2) + (-1)^2 P(Y = -1) + (1)^2 P(Y = 1) + (2)^2 P(Y = 2) \\ &= 4 \cdot 0.25 + 1 \cdot 0.25 + 1 \cdot 0.25 + 4 \cdot 0.25\\ &= 2.5 \end{aligned} \end{split}\]كما توقعنا، التباين في $ Y $ أكبر من التباين في $ X $.
لدى التباين خاصية مفيده لتسهل من بعض العمليات الرياضية. إذا كانت $ X $ متغير عشوائي:
\[\begin{aligned} Var(aX + b) &= a^2 Var(X) \end{aligned}\]إذا كان لدينا متغيرين عشوائيين $ X $ و $ Y $ مستقلان:
\[\begin{aligned} Var(X + Y) = Var(X) + Var(Y) \end{aligned}\]لاحظ أن خطية التوقع يمكن تطبيقها على $ X $ و $ Y $ حتى لو كانا غير مستقلان. ولكن، $ Var(X + Y) = Var(X) + Var(Y) $ لا يمكن أن تطبق إلا إذا كانا مستقلان.
التغاير
التغاير لمتغيرين عشوائيين $ X $ و $ Y $ نعرفها كالآتي:
\[\begin{aligned} Cov(X, Y) &= \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] \end{aligned}\]مرة أخرى، يمكننا القيام ببعض العمليات الرياضية ونحصل على التالي:
\[\begin{aligned} Cov(X, Y) = \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y] \end{aligned}\]لاحظ أنه على الرغم أن التباين للمتغير العشوائي يجب أن يكون رقم إيجابي، التغاير لمتغيرين عشوائيين يمكن أن يكون سلبي. بالأصح، التغاير يساعد على قياس العلاقة بين متغيرين؛ علامة نتيجة حساب التغاير تساعدنا على معرفة العلاقة بين المتغيرين إذا كانت إيجابية أو سلبية. إذا كانا المتغيرين $ X $ و $ Y $ مستقلين، فإن $ Cov(X, Y) = 0 $ و $ \mathbb{E}[XY] = \mathbb{E}[X]\mathbb{E}[Y] $
متغيرات برنولي العشوائية
لنفترض أننا نستخدم المتغير العشوائي $ X $ لتمثيل عملية رمي العملة المعدنية بشكل منحاز وفيها $ P(Heads) = p $. يمكننا القول إن $ X = 1 $ إذا كان رمي العملة يؤدي إلى صوره، و $ X = 0 $ إذا كان رمي العملة يؤدي إلى كتابه. لذا، $ P(X = 1) = p $ و $ P(X = 0) = 1 - p $. هذا النوع من المتغيرات العشوائية الثنائية يطلق عليه نافير برنولي العشوائي؛ يمكننا حساب القيمة المتوقعة والتباين بالطريقة التالية: 📝
\[\mathbb{E}[X] = 1 \times p + 0 \times (1 - p) = p\] \[\begin{split} \begin{aligned} Var(X) &= \mathbb{E}[X^2] - \mathbb{E}[X]^2 \\ &= 1^2 \times p + 0^2 \times (1 - p) - p^2 \\ &= p - p^2 \\ &= p(1 - p) \end{aligned} \end{split}\]متوسط العينة
لنفترض أن لدينا عملة معدنية مُنحازة وفيها $ P(Heads) = p $ ونريد أن نتوقع $ p $. يمكننا رمي العملة $ n $ مرات وأخذ عينة من الرميات وحساب نسبة ظهور الصورة في عينتنا، نسميها $ \hat p $. إذا عرفنا أن $ \hat p $ أقرب بشكل أكثر أن تكون $ p $ (صوره)، يمكننا استخدام $ \hat p $ كوسيلة توقع أو تقدير ل $ p $.
لاحظ أن $ p $ ليست قيمه عشوائية؛ هي قيمه ثابتة بناءًا على الانحياز في عملتنا المعدنية. $ \hat p $ هي قيمه عشوائية كونها تتكون من الرمي العشوائي للعملة المعدنية. لذا، يمكننا حساب التوقع والتباين ل $ \hat p $ لنعرف مدى جودة تقديره ل $ p $.
لحساب $ \mathbb{E}[\hat p] $، سنحتاج أولاً لتعريف المتغيرات العشوائية لكل عملية رمي للعملة المعدنية في عينتنا. لتكون $ X_i $ هي متغير برنولي العشوائي للقيمة $ i^{th} $ من رمي العملة. إذا، نعرف أن:
\[\begin{aligned} \hat p = \frac{X_1 + X_2 + \ldots + X_n}{n} \end{aligned}\]لحساب التوقع ل $ \hat p $، يمكننا تعويض المعادلة في الأعلى ونستخدم ما نعرفه أن $ \mathbb{E}[X_i] = p $ بما أن $ X_i $ هي متغير برنولي العشوائي.
\[\begin{split} \begin{aligned} \mathbb{E}[\hat p] &= \mathbb{E} \left[ \frac{X_1 + X_2 + \ldots + X_n}{n} \right] \\ &= \frac{1}{n} \mathbb{E}[X_1 + \ldots + X_n] \\ &= \frac{1}{n} \left( \mathbb{E}[X_1] + \ldots + \mathbb{E}[X_n] \right) \\ &= \frac{1}{n} (p + \ldots + p) \\ &= \frac{1}{n} (np) \\ \mathbb{E}[\hat p] &= p \end{aligned} \end{split}\]وجدنا أن $ \mathbb{E}[\hat p] = p $. بمعنى آخر، بعد كافي من عمليات رمي للعملة نتوقع أن $ \hat p $ ستتلاقى مع الانحياز الحقيقي في العملة $ p $. نقول إن $ \hat p $ هي متوقع (مقدر) غير متحيز Unbiased Estimator ل $ p $.
الآن، نقوم بحساب التباين ل $ \hat p $. بما أن كل عملية رمي للعملة هي عملية مستقلة عن باقي الرميات، فأننا نعرف أن $ X_i $ هي مستقلة. ذلك يُمكننا من استخدام خطية التباين:
\[\begin{split} \begin{aligned} Var(\hat p) &= Var \left(\frac{1}{n} \sum_{i=1}^{n} X_i \right) \\ &= \frac{1}{n^2} \sum_{i=1}^{n}Var(X_i) \\ &= \frac{1}{n^2} \times np(1-p) \\ Var(\hat p) &= \frac{p(1-p)}{n} \end{aligned} \end{split}\]من المعادلة السابقة، نرى أن أداة التوقع لدينا تباينها يقل كلما زادت $ n $، عدد مرات الرمي في عينتنا. بمعنى آخر، إذا قمنا بجمع الكثير من البيانات فسنكون متأكدين من نتائج أداة توقعنا. يعرف ذلك بقاعدة الأرقام الكبيرة. 📝 📝
ملخص التوقع والتباين
استخدمنا التوقع والتباين لشرح بشكل بسيط متوسط وانتشار العينة العشوائية. هذه الأدوات الرياضية تساعدنا على تحديد مدى كفاءة قيمه محسوبة من العينة على توقع باقي المجتمع الإحصائي.
التقليل من دالة الخسارة يكون لنا نموذجاً دقيقاً على بيانات التدريب. التوقع والتباين يساعدنا على إظهار بيانات عن دقة النموذج عندما يرى بيانات جديده من المجتمع الإحصائي.
المخاطر
في مثال لأحد النماذج التي تحدثنا عنها في الفصول السابقة، النادل قام بجمع بيانات الإكراميات التي حصل عليها في إحدى الشهور. قمنا باختيار نموذج وتقليل دالة الخسارة للخطأ التربيعي المتوسط (MSE)، لنتأكد أن نموذجنا يقدم نتائج أفضل من بقية النماذج الأخرى على هذه البيانات. لهذا النموذج متغير واحد فقط وهو $ \theta $. وجدنا أيضاً أن متغير التحسين لدالة الخسارة MSE هو $ \hat{\theta} = \text{mean}(\textbf y) $.
على الرغم أن مثل هذه النماذج تقدم توقعات وتنبؤات صحيحه على بيانات التدريب، نريد أن نعرف ما إذا كان النموذج يستطيع القيام بنفس الأداء على بيانات جديده من المجتمع الإحصائي للبدء في التعامل مع هذه المشكلة، سنتعرف على المصطلح الإحصائي المخاطر Risk، وتعرف أيضاً ب الخسارة المتوقعة Expected Loss. 📝
التعريف
مخاطر النموذج هي الخسارة المتوقعه للنموذج عند تجربته على قيمه عشوائية من المجتمع الأحصائي.
في مثالنا، المجتمع الإحصائي هو جميع الإكراميات التي حصل عليها النادل طوال فترة عمله، بما فيها الإكراميات المستقبليه. نستخدم المتغير العشوائي $ X $ لتمثيل نسبة الإكرامية العشوائية المختاره من المجتمع، والمتغير $ \theta $ يمثل توقع النموذج. بإستخدام هذه الرموز، فأن المخاطر $ R(\theta) $ لنموذجنا هي:
\[\begin{aligned} R(\theta) = \mathbb{E}\left[(X - \theta)^2\right] \end{aligned}\]في المعادلة، استخدمنا دالة الخسارة ل MSE والتي تعطينا $ (X - \theta)^2 $. المخاطر هي دالة $ \theta $ كوننا نتحكم بمحتوى $ \theta $ كما يحلو لنا.
على عكس الخسارة، استخدام المخاطر يسمح لنا بتحديد أسباب دقة النموذج على المجتمع بشكل عام. إذا كانت نتيجة المخاطر لنموذجنا قليله، فأنه سيقوم بتنبؤات صحيحه على بيانات المجتمع على المدى البعيد. في الجانب الآخر، إذا كانت المخاطر لنموذجنا عاليه فإن أداءه على بيانات المجتمع سيكون ضعيفاً.
بالطبع، نحاول أن نختار قيمه ل $ \theta $ تجعل مخاطر النموذج أقل ما يمكن. نستخدم المتغير $ \theta^* $ لتمثيل القيمة الناتجة عن استخدام $ \theta $ للحصول على أقل مخاطر، أو أفضل متغير للحصول على نموذج مثالي للبيانات. للتوضيح، $ \theta^* $ تمثل النموذج الذي يقلل المخاطر بينما $ \hat{\theta} $ تمثل المتغير الذي يقلل من دالة الخسارة للبيانات.
تقليل المخاطر
لنحاول إيجاد قيمة $ \theta $ التي تقلل من المخاطر. في السابق، كنا نستخدم التفاضل والتكامل للقيام بعملية التقليل هذه. الآن، سنستخدم أدوات رياضية ذا مصطلحات واضحة. سنبدل $ X - \theta $ ب $ X - \mathbb{E}[X] + \mathbb{E}[X] - \theta $ ونتوسع:
\[\begin{split} \begin{aligned} R(\theta) &= \mathbb{E}[(X - \theta)^2] \\ &= \mathbb{E}\left[ (X - \mathbb{E}[X] + \mathbb{E}[X] - \theta)^2 \right] \\ &= \mathbb{E}\left[ \bigl( (X - \mathbb{E}[X]) + (\mathbb{E}[X] - \theta) \bigr)^2 \right] \\ &= \mathbb{E}\left[ (X - \mathbb{E}[X])^2 + 2(X - \mathbb{E}[X])(\mathbb{E}[X] - \theta) + (\mathbb{E}[X]- \theta)^2 \right] \\ \end{aligned} \end{split}\]الآن، نطبق خطية التوقع ونبسط المعادلة. سنستخدم $ \mathbb{E}\left[ (X - \mathbb{E}[X]) \right] = 0 $ وهي تعني بشكل كبير أن $ \mathbb{E}[X] $ تقع في متوسط التوزيع ل $ X $.
\[\begin{split} \begin{aligned} R(\theta) &= \mathbb{E}\left[ (X - \mathbb{E}[X])^2 \right] + \mathbb{E}\left[ 2(X - \mathbb{E}[X])(\mathbb{E}[X] - \theta) \right] + \mathbb{E}\left[ (\mathbb{E}[X]- \theta)^2 \right] \\ &= \mathbb{E}\left[ (X - \mathbb{E}[X])^2 \right] + 2 (\mathbb{E}[X] - \theta) \underbrace{ \mathbb{E}\left[ (X - \mathbb{E}[X]) \right]}_{= 0} + (\mathbb{E}[X]- \theta)^2 \\ &= \mathbb{E}\left[ (X - \mathbb{E}[X])^2 \right] + 0 + (\mathbb{E}[X]- \theta)^2 \\ R(\theta) &= \mathbb{E}\left[ (X - \mathbb{E}[X])^2 \right] + (\mathbb{E}[X]- \theta)^2 \\ \end{aligned} \end{split}\]لاحظ أن أول مصطلح في المعادلة السابقة هو التباين Variance ل $ X $، $ Var(X) $، والذي لا يعتمد على $ \theta $. المصطلح الثاني يعطي مقياس لمدى قرب $ \theta $ من $ \mathbb{E}[X] $. بسبب ذلك، يطلق على المصطلح الثاني الانحياز Bias للنموذج. بمعنى آخر، مخاطر النموذج هي انحياز النموذج إضافة إلى التباين للكمية التي نرغب بالتنبؤ عنها:
\[\begin{aligned} R(\theta) &= \underbrace{(\mathbb{E}[X]- \theta)^2}_\text{bias} + \underbrace{Var(X)}_\text{variance} \end{aligned}\]ولذلك، تكون المخاطر أقل عندما لا يكون نموذجنا مُنحاز: $ \theta^* = \mathbb{E}[X] $
تحليل المخاطر
لاحظ عندما يكون نموذجنا دون تحيز، المخاطر تكون إيجابية. ذلك يعني أنه حتى النموذج المثالي سيحصل على توقعات خاطئة. ذلك يحدث لأن النموذج سيتنبأ بقيمه واحدة فقط بينما $ X $ قد تأخذ أي قيمه من المجتمع الإحصائي. التباين يبين لنا حجم وكمية الخطأ. إذا كان التباين قليل يعني أن $ X $ ستكون قيمه قريبه من $ \theta $، وعندما يكون التباين عالي فيعني أن $ X $ ستكون قيمه بعيدة عن $ \theta $.
تقليل المخاطر التجريبية
من التحليل السابق، نريد تعيين $ \theta = \mathbb{E}[X] $. للأسف، لحساب $ \mathbb{E}[X] $ نحتاج لمعرفة كل شيء عن المجتمع الإحصائي. لمعرفة السبب، تحقق من التعبير التالي ل $ \mathbb{E}[X] $:
\[\begin{aligned} \mathbb{E}[X] = \sum_{x \in \mathbb{X}} x \cdot P(X = x) \end{aligned}\]تمثل $ P(X = x) $ احتمالية أن $ X $ تأخذ قيمه معينة من المجتمع الإحصائي. لكن، لحساب الاحتمالية، نحتاج لمعرفة جميع القيم التي يمكن أن تأخذها $ X $ وعدد مرات ظهورها في المجتمع الإحصائي. بمعنى آخر، لتقليل المخاطر في النموذج بشكل مُتقن، نحتاج أن تتوفر لدينا بيانات المجتمع الإحصائي
يمكننا مواجهة هذه المشكلة عن طريق معرفة أن توزيع القيم في عينة عشوائية كبيرة سيكون قريباً من توزيع القيم في المجتمع الإحصائي. إذا كان لذلك صحيحاً في عينتنا، يمكننا التعامل مع العينة كأنها كامل المجتمع الإحصائي.
لنفترض أننا رسمنا نقاطاً بشكل عشوائي من العينة بدلاً من المجتمع الإحصائي. بما أن لدينا عدد $ n $ من النقاط في العينة $ \mathbf{x} = { x_1, x_2, \ldots, x_n } $، كل نقطة $ x_i $ لديها احتمالية تساوي $ \frac{1}{n} $ للظهور. الآن يمكننا كتابة توقع ل $ \mathbb{E}[X] $:
\[\begin{aligned} \mathbb{E}[X] &\approx \frac{1}{n} \sum_{i=1}^n x_i = \text{mean}({\mathbf{x}}) \end{aligned}\]لذا، توقعنا المناسب ل $ \theta^* $ باستخدام المعلومات من العينة العشوائية هو أن $ \hat{\theta} = \text{mean}(\mathbf{x}) $. نقول إن $ \hat{\theta} $ تقلل من المخاطر التجريبية Empirical Risk، وهي المخاطر التي تم حسابها باستخدام العينة كبديل عن المجتمع الإحصائي.
أهمية العينات العشوائية
يجب أن نلاحظ أهمية العينة العشوائية في المثال السابق. إذا كانت العينة غير عشوائية، لن نستطيع إثبات الفرضية السابقة أن توزيع العينة يشابه توزيع المجتمع الإحصائي. باستخدام عينه غير عشوائية لتوقع $ \theta^* $ ستكون النتائج عادةً منحازة وذات مخاطر أعلى.
العلاقة مع تقليل الخسارة
لنتذكر أننا شرحنا مسبقاً بأن $ \hat{\theta} = \text{mean}(\mathbf{x}) $ تقلل من دالة الخسارة MSE في البيانات. الآن، أخذنا خطوه جادة إلى الأمام. إذا كانت بيانات التدريب هي عينه عشوائية، فإن $ \hat{\theta} = \text{mean}(\mathbf{x}) $ لن تكون لنا النموذج المثالي فقط لبيانات التدريب ولكن أيضاً لكامل المجتمع الإحصائي، بالأخذ بالاعتبار المعلومات التي لدينا عن العينة.
ملخص المخاطر
باستخدام الأدوات الرياضية التي طورناها في هذا الفصل، تعرفنا على أداء النموذج على المجتمع الإحصائي. النموذج يكون ذو تنبؤات دقيقة إذا كانت المخاطر الإحصائية Statistical Risk أقل. وجدنا أن المتغير للنموذج المثالي هو:
\[\begin{aligned} \theta^* = \mathbb{E}[X] \end{aligned}\]بما أننا لا نستطيع القيام بعملية الحساب بسهوله، وجدنا متغير النموذج الذي يقلل من المخاطر التجريبية Empirical Risk:
\[\begin{aligned} \hat \theta = \text{mean}(\mathbf x) \end{aligned}\]إذا كانت بيانات التدريب أخذت بشكل عشوائي من المجتمع الإحصائي، فغالباً $ \hat{\theta} \approx \theta^* $. لذا، النموذج الذي يتم تدريبه باستخدام بيانات عشوائية ضخمة من المجتمع الإحصائي غالباً ما يؤدي بشكل ممتاز على كامل المجتمع الإحصائي.