مبادئ وتقنيات علم البيانات
الفصل الثالث عشر: النماذج الخطية
فهرس الفصل:
مقدمة
الآن، بعد أن تعلمنا بشكل عام أدوات لضبط النماذج مع دوال التكلفة، نتحول لطرق تحسين النموذج. للتبسيط، في السابق حددنا عملنا على النموذج الثابت: نموذجنا فقط يتوقع رقم واحد.
ولكن، إعطاء نموذج كهذا للنادل لن يرضيه. يود النادل أن يوضح أنه حصل على معلومات أكثر نسبة الإكرامية من الطاولات التي خدمها. لماذا لا نستخدم بياناته الأخرى، مثلاً حجم العملاء في الطاولة ومجموع الفاتورة، لغرض جعل النموذج أكثر فائدة.
في هذا الفصل سنتعرف على النماذج الخطية والذي يسمح لنا باستخدام جميع البيانات التي لدينا لإجراء توقعات. النماذج الخطية لا تستخدم بنطاقٍ واسع فقط، بل أيضاً لديها أسس نظرية غنية بالمعلومات التي تجعلنا نفهم أدوات مستقبليه للنماذج. سنتعرف على نموذج الانحدار الخطي البسيط الذي يستخدم متغير واحد، سنتعلم كيف يستخدم النزول الاشتقاقي لضبط النموذج، وأخيراً التوسع في النموذج وإضافة المزيد من المتغيرات له.
التنبؤ بالإكراميات
سابقاً، تعاملنا مع بيانات تحتوي على صف واحد لكل طاولة قام النادل بخدمتها لمدة أسبوع. النادل قام بجمع البيانات للقيام بالتوقع بقيمة الإكرامية التي سيحصل عليها في المستقبل:
tips = sns.load_dataset('tips')
tips.head()
| size | time | day | smoker | sex | tip | total_bill | |
|---|---|---|---|---|---|---|---|
| 2 | Dinner | Sun | No | Female | 1.01 | 16.99 | 0 |
| 3 | Dinner | Sun | No | Male | 1.66 | 10.34 | 1 |
| 3 | Dinner | Sun | No | Male | 3.5 | 21.01 | 2 |
| 2 | Dinner | Sun | No | Male | 3.31 | 23.68 | 3 |
| 4 | Dinner | Sun | No | Female | 3.61 | 24.59 | 4 |
sns.distplot(tips['tip'], bins=25);
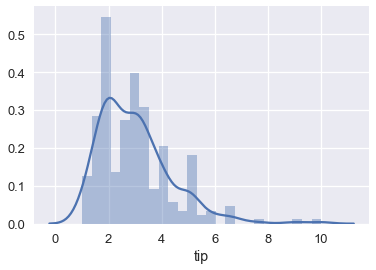
كما تحدثنا سابقاً، إذا اخترنا النموذج الثابت ودالة الخطأ التربيعي المتوسط، فإن نموذجنا سيتوقع متوسط الإكراميات:
np.mean(tips['tip'])
2.9982786885245902
يعني ذلك أن عندما يأتي مجموعة من الزبائن للنادل ثم يسألنا النادل عن مجموعه الإكرامية التي سيحصل عليها، فسنجيب عليه “حوالي $ \$3 $”، أياً كان عدد الزبائن ومجموع الفاتورة.
ولكن، عند التحقق من باقي المتغيرات في البيانات، يمكننا أن نقوم بتوقعات دقيقه إذا أضفنا تلك المتغيرات للنموذج. مثلاً، الرسم البياني التالي يوضح مجموع الإكرامية مقارنة بمبلغ الفاتورة ويظهر العلاقة الإيجابية بينهما:
sns.lmplot(x='total_bill', y='tip', data=tips, fit_reg=False)
plt.title('Tip amount vs. Total Bill')
plt.xlabel('Total Bill')
plt.ylabel('Tip Amount');
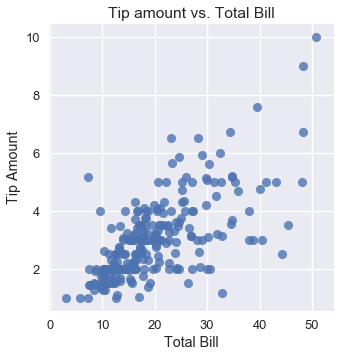
على الرغم من أن متوسط الإكرامية هو $ \$3 $، إذا كانت الطاولة طلبت ما مجموعه $ \$40 $ من الوجبات فأننا متأكدين أن النادل سيحصل على أكثر من $ \$3 $ كإكرامية. لذا، نريد التعديل في نموذجنا ليتمكن من التوقع بناءًا على متغيرات في بياناتنا بدلاً من توقع متوسط الإكرامية. للقيام بذلك، سنستخدم النموذج الخطي بدلاً من الثابت.
لنراجع أولاً الأدوات التي لدينا لبناء النموذج والتوقع وتعريف بعض الرموز الجديدة لنتمكن بشكل أفضل من تمثيل العمليات الرياضية الإضافية في النموذج الخطي.
تعريف نموذج خطي بسيط
نحن مهتمون بتوقع قيمة الإكرامية بناءًا على مجموع الفاتورة. لنجعل $ y $ تمثل مجموع الإكرامية، المتغير الذي نريد أن يتوقعه النموذج. و $ x $ تمثل مجموع الفاتورة، المتغير الذي نريد استخدامه للتوقع.
نقوم بتعريف النموذج الخطي $ f_\boldsymbol\theta^* $ الذي يعتمد على $ x $:
\[f_\boldsymbol\theta^* (x) = \theta_1^* x + \theta_0^*\]نتعامل مع $ f_\boldsymbol\theta^* (x) $ على أنها الدالة التي أنشأت البيانات.
تفترض $ f_\boldsymbol\theta^* (x) $ أن $ y $ لديها علاقة خطيه كاملة مع $ x $. ولكن، في بياناتنا لا يظهر لنا خط مستقيم بسبب وجود بعض البيانات العشوائية المزعجة $ \epsilon $. رياضياً، نأخذ بعين الاعتبار هذه المشكلة بإضافة المصطلح:
\[y = f_\boldsymbol\theta^* (x) + \epsilon\]إذا كانت الافتراضية أن $ y $ لديها علاقه خطية كاملة مع $ x $، وتمكنا بطريقة ما من توقع القيمة الصحيحة ل $ \theta_1^* $ و $ \theta_0^* $، وبشكل غير اعتيادي لم يكنا لدينا أي عشوائية في البيانات، سنتمكن من التوقع بشكل دقيق قيمة الإكرامية التي سيحصل عليها النادل من جميع الزبائن، وبشكل دائم. بالطبع، لا يمكننا تلبية جميع المعايير في الواقع. بدلاً من ذلك، نتوقع $ \theta_1^* $ و $ \theta_0^* $ باستخدام البيانات لجعل توقعاتنا أقرب دقه للواقع.
توقع النموذج الخطي
بما أننا لا نستطيع إيجاد قيمة $ \theta_1^* $ و $ \theta_0^* $ بشكل دقيق، سنفترض أن بياناتنا تتوقع قيمة هذه المتغيرات. نشير للتوقعات ب $ \theta_1 $ و $ \theta_0 $، وتوقعنا الذي يتم ضبطه بالنموذج ب $ \hat{\theta_1} $ و $ \hat{\theta_0} $، و النموذج:
\[f_\boldsymbol\theta (x) = \theta_1 x + \theta_0\]أحياناً سترى $ h(x) $ بدلاً من $ f_\hat{\boldsymbol\theta} (x) $؛ ال $ h $ تعني الفرضية Hypothesis، كون $ f_\hat{\boldsymbol\theta} (x) $ هي فرضيتنا ل $ f_{\boldsymbol\theta^*} (x) $.
من أجل تحديد قيمة $ \hat{\theta_1} $ و $ \hat{\theta_0} $، نقوم باختيار دالة تكلفة وتقليلها باستخدام النزول الاشتقاقي.
ضبط النموذج الخطي باستخدام النزول الاشتقاقي
نريد ضبط نموذج خطي يتنبأ بقيمة الإكرامية من مجموع الفاتورة:
\[f_\boldsymbol\theta (x) = \theta_1 x + \theta_0\]ولتحسين قيم $ \theta_1 $ و $ \theta_0 $، نحتاج أولاً لاختيار دالة خسارة. سنختار دالة خسارة الخطأ التربيعي المتوسط MSE:
\[\begin{split} \begin{aligned} L(\boldsymbol\theta, \textbf{x}, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - f_\boldsymbol\theta (x_i))^2\\ \end{aligned} \end{split}\]لاحظ أننا عدلنا على دالة الخسارة لتوضيح إضافتنا لمتغير في النموذج. الآن، $ \textbf{x} $ هي مصفوفة أحادية البعد تحتوي على جميع الفواتير، و $ \textbf{y} $ هي مصفوفة أحادية البعد تحتوي على قيمة كل إكرامية، و $ \boldsymbol\theta $ هي مصفوفة تحتوي على التالي: $ \boldsymbol\theta = [ \theta_1, \theta_0 ] $.
يطلق على استخدام النموذج الخطي مع دالة خسارة الخطأ التربيعي المتوسط بإسم الانحدار الخطي للمربعات الصغرى Least-squares Linear Regression. يمكننا استخدام النزول الاشتقاقي لإيجاد قيمة $ \boldsymbol\theta $ التي تقلل الخسارة. 📝
ملاحظة عن استخدام العلاقات
إذا سبق أن رأيت الانحدار الخطي للمربعات الصغرى، قد تلاحظ أننا نستطيع حساب معامل الارتباط واستخدامه لتحديد قيمة $ \theta_1 $ و $ \theta_0 $. هذه طريقة أسهل وأسرع للحساب بدلاً من استخدام النزول الاشتقاقي في أي معادله، تماماً كما يكون أسهل لنا حساب المتوسط بدلاً من حساب النزول الاشتقاقي لضبط النموذج الثابت. على أية حال، سنستخدم النزول الاشتقاقي لأنها طريقة عامله لتقليل الخسارة وستعمل معنا لاحقاً عندما نتعرف على نماذج لا يمكن حساب خسارتها إحصائياً. بالأصح، في كثير من المشاكل في العالم الحقيقي، سنستخدم النزول الاشتقاقي حتى ولو كانت هناك طرق إحصائية تحليله لأن حسابها يأخذ وقتاً أطول من النزول الاشتقاقي، خاصة عندما تكون البيانات ذات حجم كبير.
مشتقة خسارة الخطأ التربيعي المتوسط MSE
لاستخدام النزول الاشتقاقي، نحتاج لحساب مشتقة خسارة الخطأ التربيعي المتوسط بالنسبة ل $ \boldsymbol\theta $. الآن بما أن $ \boldsymbol\theta $ عبارة عن مصفوفة ذات طول 2 وليست قيمة عددية مدرجة Scalar، و $ \nabla_{\boldsymbol\theta} L(\boldsymbol\theta, \textbf{x}, \textbf{y}) $ أيضاً مصفوفة من الحجم 2. 📝
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} L(\boldsymbol\theta, \textbf{x}, \textbf{y}) &= \nabla_{\boldsymbol\theta} \left[ \frac{1}{n} \sum_{i = 1}^{n}(y_i - f_\boldsymbol\theta (x_i))^2 \right] \\ &= \frac{1}{n} \sum_{i = 1}^{n}2 (y_i - f_\boldsymbol\theta (x_i))(- \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (x_i))\\ &= -\frac{2}{n} \sum_{i = 1}^{n}(y_i - f_\boldsymbol\theta (x_i))(\nabla_{\boldsymbol\theta} f_\boldsymbol\theta (x_i))\\ \end{aligned} \end{split}\]نعرف أن:
\[f_\boldsymbol\theta (x) = \theta_1 x + \theta_0\]نريد حساب قيمة $ \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (x_i) $ والتي هي مصفوفة طولها 2:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (x_i) &= \begin{bmatrix} \frac{\partial}{\partial \theta_0} f_\boldsymbol\theta (x_i)\\ \frac{\partial}{\partial \theta_1} f_\boldsymbol\theta (x_i) \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial}{\partial \theta_0} [\theta_1 x_i + \theta_0]\\ \frac{\partial}{\partial \theta_1} [\theta_1 x_i + \theta_0] \end{bmatrix} \\ &= \begin{bmatrix} 1 \\ x_i \end{bmatrix} \\ \end{aligned} \end{split}\]أخيراً، نعوضها في معادلتنا الأساسية لنحصل على التالي:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} L(\theta, \textbf{x}, \textbf{y}) &= -\frac{2}{n} \sum_{i = 1}^{n}(y_i - f_\boldsymbol\theta (x_i))(\nabla_{\boldsymbol\theta} f_\boldsymbol\theta (x_i))\\ &= -\frac{2}{n} \sum_{i = 1}^{n} (y_i - f_\boldsymbol\theta (x_i)) \begin{bmatrix} 1 \\ x_i \end{bmatrix} \\ &= -\frac{2}{n} \sum_{i = 1}^{n} \begin{bmatrix} (y_i - f_\boldsymbol\theta (x_i)) \\ (y_i - f_\boldsymbol\theta (x_i)) x_i \end{bmatrix} \\ \end{aligned} \end{split}\]هذه مصفوفة من طولها 2 كون $ (y_i - f_\boldsymbol\theta (x_i)) $ قيمة عددية مدرجه.
تطبيق النزول الاشتقاقي
الآن، لنقوم بضبط النموذج الخطي على بيانات الإكراميات لتوقع قيمة الإكرامية من مجموع الفاتورة.
أولاً، نقوم بتعريف دالة في بايثون لحساب الخسارة:
def simple_linear_model(thetas, x_vals):
'''نتيجة هذه الداله هي القيمه المتوقعه من النموذج الخطي'''
return thetas[0] + thetas[1] * x_vals
def mse_loss(thetas, x_vals, y_vals):
return np.mean((y_vals - simple_linear_model(thetas, x_vals)) ** 2)
ثم نعرف دالة تقوم بحساب خطية الخسارة:
def grad_mse_loss(thetas, x_vals, y_vals):
n = len(x_vals)
grad_0 = y_vals - simple_linear_model(thetas, x_vals)
grad_1 = (y_vals - simple_linear_model(thetas, x_vals)) * x_vals
return -2 / n * np.array([np.sum(grad_0), np.sum(grad_1)])
سنقوم باستخدام الدالة minimize التي سبق أن عرفناها لتطبيق النزول الاشتقاقي:
def minimize(loss_fn, grad_loss_fn, x_vals, y_vals,
alpha=0.0005, progress=True):
# تستخدم النزول الاشتقاقي للتقليل من دالة الخسارة loss_fn.
# تنتج لنا الداله القيمه الصغرى ل theta_hat (θ^) عندما يكون
# التغيير اقل من 0.001 بين التكرارات.
theta = np.array([0., 0.])
loss = loss_fn(theta, x_vals, y_vals)
while True:
if progress:
print(f'theta: {theta} | loss: {loss}')
gradient = grad_loss_fn(theta, x_vals, y_vals)
new_theta = theta - alpha * gradient
new_loss = loss_fn(new_theta, x_vals, y_vals)
if abs(new_loss - loss) < 0.0001:
return new_theta
theta = new_theta
loss = new_loss
والآن نقوم بتطبيق النزول الاشتقاقي:
thetas = minimize(mse_loss, grad_mse_loss, tips['total_bill'], tips['tip'])
theta: [0. 0.] | cost: 10.896283606557377
theta: [0. 0.07] | cost: 3.8937622006094705
theta: [0. 0.1] | cost: 1.9359443267168215
theta: [0.01 0.12] | cost: 1.388538448286097
theta: [0.01 0.13] | cost: 1.235459416905535
theta: [0.01 0.14] | cost: 1.1926273731479433
theta: [0.01 0.14] | cost: 1.1806184944517062
theta: [0.01 0.14] | cost: 1.177227251696266
theta: [0.01 0.14] | cost: 1.1762453624313751
theta: [0.01 0.14] | cost: 1.1759370980989148
theta: [0.01 0.14] | cost: 1.175817178966766
نلاحظ أن النزول الاشتقاقي يقترب لقيمة $ \hat\theta_0 = 0.01 $ و $ \hat\theta_0 = 0.14 $. نموذجنا الخطي الآن:
\[y = 0.14x + 0.01\]يمكننا استخدام النتيجة السابقة لرسم توقعاتنا بجانب البيانات الحقيقية:
x_vals = np.array([0, 55])
sns.lmplot(x='total_bill', y='tip', data=tips, fit_reg=False)
plt.plot(x_vals, simple_linear_model(thetas, x_vals), c='goldenrod')
plt.title('Tip amount vs. Total Bill')
plt.xlabel('Total Bill')
plt.ylabel('Tip Amount');
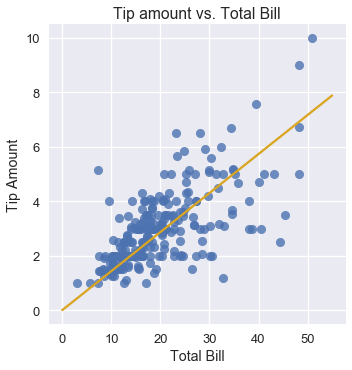
نلاحظ أنه عندما تكون قيمة الفاتورة $ \$10 $، فإن نموذجنا يتوقع أن النادل سيحصل على إكرامية بحوالي $ \$1.50 $. بنفس الطريقة، إذا كانت قيمة الفاتورة $ \$40 $ فإن النموذج يتوقع حصول النادل على إكرامية بقيمة $ \$6.00 $.
الانحدار الخطي المتعدد
نموذجنا الخطي البسيط لميزة إضافية عن النموذج الثابت، الميزة هي استخدامه البيانات للتوقع. ولكن، لا يزال النموذج محدود كونه يستخدم متغير واحد من بياناتنا. الكثير من البيانات تحتوي على أكثر من متغير مهم ومفيد للاستخدام، ويمكن للانحدار الخطي المتعدد الاستفادة من ذلك. مثلاً، لنأخذ البيانات التالية لأنواع السيارات ومعلومات صرف الوقود بالميل لكل جالون (Milage Per Gallon MPG):
لتحميل قاعدة البيانات mpg.csv اضغط هنا.
mpg = pd.read_csv('mpg.csv').dropna().reset_index(drop=True)
mpg
| car name | origin | model year | ... | displacement | cylinders | mpg | |
|---|---|---|---|---|---|---|---|
| chevrolet chevelle malibu | 1 | 70 | ... | 307 | 8 | 18 | 0 |
| buick skylark 320 | 1 | 70 | ... | 350 | 8 | 15 | 1 |
| plymouth satellite | 1 | 70 | ... | 318 | 8 | 18 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| dodge rampage | 1 | 82 | ... | 135 | 4 | 32 | 389 |
| ford ranger | 1 | 82 | ... | 120 | 4 | 28 | 390 |
| chevy s-10 | 1 | 82 | ... | 119 | 4 | 31 | 391 |
392 rows × 9 columns
يبدو لنا أن أكثر من متغير يؤثر على صرف السيارة للوقود. مثلاً، يبدو أن صرف الوقود يقل عندما تزيد قوة الحصان للسيارة:
sns.lmplot(x='horsepower', y='mpg', data=mpg);
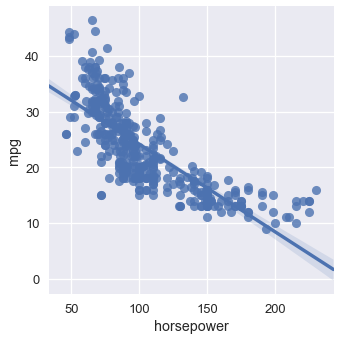
ولكن، السيارات التي في السنوات الأخيرة لديها صرف وقود أفضل بشكل عام عن السيارات القديمة:
sns.lmplot(x='model year', y='mpg', data=mpg);
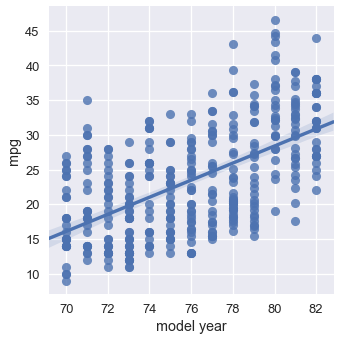
يظهر أن بإمكاننا الحصول على نتائج أكثر دقة للنموذج إذا استطعنا استخدام قوة الحصان وسنة صناعة السيارة للتنبؤ عن كمية صرف الوقود بالميل لكل جالون MPG. بالأصح، يبدو أن النموذج المثالي يأخذ بعين الاعتبار جميع المتغيرات الرقمية في بياناتنا. يمكننا توسيع نموذجنا الخطي ذو المتغير الواحد ليتمكن من التنبؤ بناءًا على أي عدد من المتغيرات.
ذكرنا أن تعريف النموذج كالتالي:
\[f_\boldsymbol\theta (\textbf{x}) = \theta_0 + \theta_1 x_1 + \ldots + \theta_p x_p\]فيها $ \textbf{x} $ تمثل متّجهة Vector تحتوي على عدد $ p $ من المتغيرات لسيارة واحدة. النموذج السابق يقول التالي، “خذ أكثر من متغير عن السيارة، اضربهم بوزن Weight معين، ثم أجمعهم معاً للقيام بتوقع صرفية السيارة للوقود بالميل لكل جالون”.
توجد أنواع متعددة من طرق تمثيل الأرقام: 📝
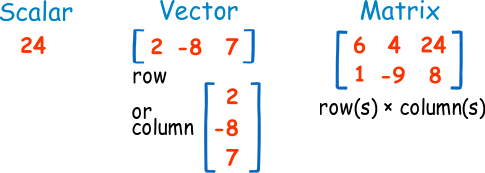
- عدد Scalar: رقم صحيح مثلاً $ 7, -4, 0.345 $.
- المتّجه Vector: هي مصفوفة أرقام أحادية الأبعاد، تكون إما من صف واحد أو عمود واحد.
- مصفوفة Matrix: مصفوفة أرقام تحتوي على أكثر من صف أو عمود.
مثلاً، إذا أردنا إجراء توقع لأول سيارة في بياناتنا باستخدام قوة الحصان، الوزن، وسنة الصناعة، فسيكون شكل المتّجهة $ \textbf{x} $ كالتالي:
mpg.loc[0:0, ['horsepower', 'weight', 'model year']]
| model year | weight | horsepower | |
|---|---|---|---|
| 70 | 3504.0 | 130.0 | 0 |
في هذا المثال أبقينا أسماء الأعمدة للتوضيح، ولكن تذكر أن $ \textbf{x} $ تحتوي فقط على القيم الرقمية من الجدول السابق: $ \textbf{x} = [130.0, 3504.0, 70] $.
الآن، سنقوم بتعريف طريقه حسابية ستسهل العمليات الحسابية القادمة. سنقوم بإضافة الرقم $ 1 $ إلى المتّجهة $ \textbf{x} $، وسيكون شكل الصف كالتالي:
mpg_mat = mpg.assign(bias=1)
mpg_mat.loc[0:0, ['bias', 'horsepower', 'weight', 'model year']]
| model year | weight | horsepower | bias | |
|---|---|---|---|---|
| 70 | 3504.0 | 130.0 | 1 | 0 |
الآن، لاحظ ما سيحدث للعملية الحسابية لنموذجنا:
\[\begin{split} \begin{aligned} f_\boldsymbol\theta (\textbf{x}) &= \theta_0 + \theta_1 x_1 + \ldots + \theta_p x_p \\ &= \theta_0 (1) + \theta_1 x_1 + \ldots + \theta_p x_p \\ &= \theta_0 x_0 + \theta_1 x_1 + \ldots + \theta_p x_p \\ f_\boldsymbol\theta (\textbf{x}) &= \boldsymbol\theta \cdot \textbf{x} \end{aligned} \end{split}\]فيها $ \boldsymbol\theta \cdot \textbf{x} $ هي متّجه لحاصل ضرب $ \boldsymbol\theta $ و $ \textbf{x} $. صُممت المتّجهات والمصفوفات لكتابة التركيبات الخطية ولذلك فهي مناسبة جداً لنموذجنا الخطي. ولكن، يجب عليك من الآن وصاعدًا تذكر أن $ \boldsymbol\theta \cdot \textbf{x} $ هي حاصل ضرب متّجه بأخرى. يمكن أيضاً لنزع الشك، توسيع عملية ضرب المتجهتين إلى عملية جمع وضرب مبسطة.
الآن، نقوم بتعريف المصفوفة $ \textbf{X} $ والتي ستكون المصفوفة التي تحتوي على جميع أنواع السيارات كصفوف، وأول عمود هو قيمة التحيز Bias. مثلاً، هذه أول خمس أسطر من المصفوفة $ \textbf{X} $:
mpg_mat = mpg.assign(bias=1)
mpg_mat.loc[0:4, ['bias', 'horsepower', 'weight', 'model year']]
| model year | weight | horsepower | bias | |
|---|---|---|---|---|
| 70 | 3504.0 | 130.0 | 1 | 0 |
| 70 | 3693.0 | 165.0 | 1 | 1 |
| 70 | 3436.0 | 150.0 | 1 | 2 |
| 70 | 3433.0 | 150.0 | 1 | 3 |
| 70 | 3449.0 | 140.0 | 1 | 4 |
للتذكير مرة أخرى، المصفوفة الحقيقية $ \textbf{X} $ فقط تحتوي على القيم الرقمية من الجدول السابق.
لاحظ أن $ \textbf{X} $ تحتوي على أكثر من مُتجهة $ \textbf{x} $ فوق بعضها البعض. ليكون الوصف واضحاً، نقوم بتعريف $ \textbf{X}_{i} $ والتي ترمز للمتّجه في الصف رقم $ i $ في المصفوفة $ \textbf{X} $. نقوم بتعريف $ X_{i,j} $ والتي تمثل القيمة ذات الرقم $ j $ في الصف ذو الرقم $ i $ في المصفوفة $ \textbf{X} $. لذا، $ \textbf{X}_{i} $ هي متّجه ذات أبعاد $ p $ و $ $ \textbf{X}_{i,j} $ هي عدد. $ $ \textbf{X} $ هي مصفوفة $ n \times p $، فيها $ n $ هي عدد السيارات لدينا و $ p $ هي عدد المتغيرات لكل سيارة.
مثلاً، في الجدول السابق لدينا $ \textbf{X}_4 = [1, 140, 3449, 70] $ و $ X_{4,1} = 140 $ لذا الرموز هي مهمة عند تعريف دوال الخسارة لأننا سنحتاج إلى كلا القيمتين $ \textbf{X} $، مصفوفة البيانات المدخلة للنموذج، و $ y $، متّجه صرف الوقود بالميل لكل جالون.
- $ \textbf{X} $ هي مصفوفة Matrix.
- $ \textbf{x} $ هي متّجه Vector وهي هنا كل صف على حدة. مثلاً السطر الثاني: $ [1, 165.0, 3693.0, 70] $.
- $ j $ هي رقم صحيح Scalar مثلاً وزن السيارة في الصف الثالث $ 3436.0 $.
خسارة الخطأ التربيعي المتوسط وانحدارها
دالة خسارة الخطأ التربيعي المتوسط تأخذ متّجه بوزن $ \boldsymbol\theta $ و مدخلات على شكل مصفوفة $ \textbf{X} $، و متّجه لصرف الوقود بالميل لكل جالون لكل سيارة $ \textbf{y} $:
\[\begin{split} \begin{aligned} L(\boldsymbol\theta, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_{i}(y_i - f_\boldsymbol\theta (\textbf{X}_i))^2\\ \end{aligned} \end{split}\]أوجدنا مسبقاً مشتقة دالة خسارة الخطأ التربيعي المتوسط بالنسبة ل $ \boldsymbol\theta $:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} L(\boldsymbol\theta, \textbf{X}, \textbf{y}) &= -\frac{2}{n} \sum_{i}(y_i - f_\boldsymbol\theta (\textbf{X}_i))(\nabla_{\boldsymbol\theta} f_\boldsymbol\theta (\textbf{X}_i))\\ \end{aligned} \end{split}\]نعرف أيضاً أن:
\[\begin{split} \begin{aligned} f_\boldsymbol\theta (\textbf{x}) &= \boldsymbol\theta \cdot \textbf{x} \\ \end{aligned} \end{split}\]لنقوم بحساب $ \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (\textbf{x}) $. عملية الحساب أسهل من المتوقع لأن $ \boldsymbol\theta \cdot \textbf{x} = \theta_0 x_0 + \ldots + \theta_p x_p $ إذاً $ \frac{\partial}{\partial \theta_0}(\boldsymbol\theta \cdot \textbf{x}) = x_0 $ و $ \frac{\partial}{\partial \theta_1}(\boldsymbol\theta \cdot \textbf{x}) = x_1 $ إلى آخره:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (\textbf{x}) &= \nabla_{\boldsymbol\theta} [ \boldsymbol\theta \cdot \textbf{x} ] \\ &= \begin{bmatrix} \frac{\partial}{\partial \theta_0} (\boldsymbol\theta \cdot \textbf{x}) \\ \frac{\partial}{\partial \theta_1} (\boldsymbol\theta \cdot \textbf{x}) \\ \vdots \\ \frac{\partial}{\partial \theta_p} (\boldsymbol\theta \cdot \textbf{x}) \\ \end{bmatrix} \\ &= \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_p \end{bmatrix} \\ \nabla_{\boldsymbol\theta} f_\boldsymbol\theta (\textbf{x}) &= \textbf{x} \end{aligned} \end{split}\]أخيراً، نقوم بإدخال النتيجة لحساب الخطية:
\[\begin{split} \begin{aligned} \nabla_{\boldsymbol\theta} L(\boldsymbol\theta, \textbf{X}, \textbf{y}) &= -\frac{2}{n} \sum_{i}(y_i - f_\boldsymbol\theta (\textbf{X}_i))(\nabla_{\boldsymbol\theta} f_\boldsymbol\theta (\textbf{X}_i))\\ &= -\frac{2}{n} \sum_{i}(y_i - \boldsymbol\theta \cdot \textbf{X}_i)(\textbf{X}_i)\\ \end{aligned} \end{split}\]تذكر أنه بما أن $ y_i - \boldsymbol\theta \cdot \textbf{X}_i $ هي عدد و $ \textbf{X}_i $ هي متّجه ذات $ p $ أبعاد، الخطية $ \nabla_{\boldsymbol\theta} L(\boldsymbol\theta, \textbf{X}, \textbf{y}) $ هي أيضاً متّجه ذات $ p $ أبعاد.
رأينا نفس هذا النوع من النتائج عندما قمنا بحساب خطية الانحدار الخطي ووجدنا أنها ثنائية الأبعاد بما أن $ \boldsymbol\theta $ كانت ثنائية الأبعاد.
ضبط النموذج الخطي مع النزول الاشتقاقي
يمكننا الآن إدخال الخسارة ومشتقاتها إلى دالة النزول الاشتقاقي. كالعادة، سنقوم بتعريف النموذج، دالة الخسارة و دالة النزول الاشتقاقيمشتقتها في بايثون:
def linear_model(thetas, X):
'''Returns predictions by a linear model on x_vals.'''
return X @ thetas
def mse_loss(thetas, X, y):
return np.mean((y - linear_model(thetas, X)) ** 2)
def grad_mse_loss(thetas, X, y):
n = len(X)
return -2 / n * (X.T @ y - X.T @ X @ thetas)
استخدم الكاتب الرمز
@وهي علامة ضرب بين المصفوفات في Numpy، لذا يحتاج أن تكونXوthetasهي مصفوفات في Numpy كي يعمل الرمز@.
الآن، ببساطه يمكننا إدخال دوالنا إلى النزول الاشتقاقي:
X = (mpg_mat
.loc[:, ['bias', 'horsepower', 'weight', 'model year']]
.to_numpy())
y = mpg_mat['mpg'].to_numpy()
thetas = minimize(mse_loss, grad_mse_loss, X, y)
print(f'theta: {thetas} | loss: {mse_loss(thetas, X, y):.2f}')
theta: [ 0. 0. 0. 0.] | cost: 610.47
theta: [ 0. 0. 0.01 0. ] | cost: 178.95
theta: [ 0.01 -0.11 -0. 0.55] | cost: 15.78
theta: [ 0.01 -0.01 -0.01 0.58] | cost: 11.97
theta: [-4. -0.01 -0.01 0.63] | cost: 11.81
theta: [-13.72 -0. -0.01 0.75] | cost: 11.65
theta: [-13.72 -0. -0.01 0.75] | cost: 11.65
استخدم الكاتب في الكود البرمجي السابق الدالة
minimizeوهي مختلفة قليلاً عن السابقة، أجري عليها التعديلات التالية:from scipy.optimize import minimize as sci_min def minimize(loss_fn, grad_loss_fn, X, y, progress=True): # تستخدم دالة من مكتبة scipy للتقليل من خسارة الداله loss_fun # باستخدام نموذج من النزول الاشتقاقي theta = np.zeros(X.shape[1]) iters = 0 def objective(theta): return loss_fn(theta, X, y) def gradient(theta): return grad_loss_fn(theta, X, y) def print_theta(theta): nonlocal iters if progress and iters % progress == 0: print(f'theta: {theta} | loss: {loss_fn(theta, X, y):.2f}') iters += 1 print_theta(theta) return sci_min( objective, theta, method='BFGS', jac=gradient, callback=print_theta, tol=1e-7 ).x
بناءًا على النزول الاشتقاقي، فإن نموذجنا الخطي هو كالتالي:
\[y = -13.72 - 0.01x_2 + 0.75x_3\]الرسم البياني لتنبؤاتنا
كيف أدى نموذجنا؟ نلاحظ أن الخسارة قلت بشكل كبير (من 610 حتى 11.6). يمكننا طباعة نتائج توقع النموذج بجانب النتائج الحقيقية:
reordered = ['predicted_mpg', 'mpg', 'horsepower', 'weight', 'model year']
with_predictions = (
mpg
.assign(predicted_mpg=linear_model(thetas, X))
.loc[:, reordered]
)
with_predictions
| model year | weight | horsepower | mpg | predicted_mpg | |
|---|---|---|---|---|---|
| 70 | 3504 | 130 | 18 | 15.447125 | 0 |
| 70 | 3693 | 165 | 15 | 14.053509 | 1 |
| 70 | 3436 | 150 | 18 | 15.785576 | 2 |
| ... | ... | ... | ... | ... | ... |
| 82 | 2295 | 84 | 32 | 32.4569 | 389 |
| 82 | 2625 | 79 | 28 | 30.354143 | 390 |
| 82 | 2720 | 82 | 31 | 29.726608 | 391 |
392 rows × 5 columns
بما أننا أوجدنا $ \boldsymbol\theta $ من النزول الاشتقاقي، يمكننا أن نتأكد من أول سطر في بياناتنا أن $ \boldsymbol\theta \cdot \textbf{X}_0 $ تطابق توقعنا السابق:
print(f'Prediction for first row: '
f'{thetas[0] + thetas[1] * 130 + thetas[2] * 3504 + thetas[3] * 70:.2f}')
Prediction for first row: 15.45
يمكننا رسم الفرق بين توقعنا والنتيجة الحقيقية (النتيجة الحقيقية - التوقع):
resid = y - linear_model(thetas, X)
plt.scatter(np.arange(len(resid)), resid, s=15)
plt.title('Residuals (actual MPG - predicted MPG)')
plt.xlabel('Index of row in data')
plt.ylabel('MPG');
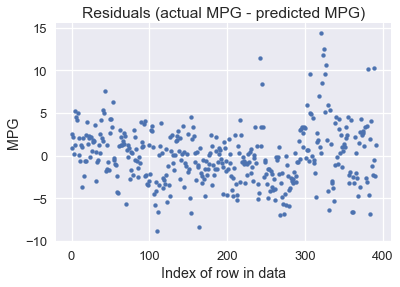
يبدو واضحاً أن نموذجنا يعطي توقعات منطقية لكثير من السيارات، على الرغم أن بعض النتائج كان الفرق فيها أكثر من 10 ميل لكل جالون (بعض السيارات لديها أقل من 10!). قد يهمنا أكثر معرفة نسبة الخط بين التوقع والنتيجة الصحيحة لصرف الوقود:
resid_prop = resid / with_predictions['mpg']
plt.scatter(np.arange(len(resid_prop)), resid_prop, s=15)
plt.title('Residual proportions (resid / actual MPG)')
plt.xlabel('Index of row in data')
plt.ylabel('Error proportion');
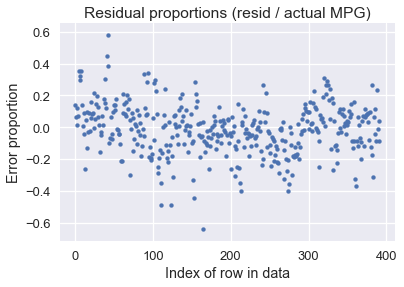
يظهر لنا أن النموذج عادةً أبعد بحدود 20% من القيمة الصحيحة.
استخدام كامل البيانات
لاحظ أن في مثالنا حتى الآن، المصفوفة $ \textbf{X} $ تحتوي على أربع أعمدة: أولها يحتوي على القيمة 1 في جميع الصفوف، عمود قوة السيارة بالحصان، وزنها، وسنة الصناعة. ولكن، يسمح لنا النموذج باستخدام أكثر من هذا العدد:
\[\begin{aligned} f_\boldsymbol\theta (\textbf{x}) &= \boldsymbol\theta \cdot \textbf{x} \end{aligned}\]عندما نضيف المزيد من الأعمدة لمصفوفتنا، نقوم بتوسيع $ \boldsymbol\theta $ لتحتوي على متغير لكل عمود في $ \textbf{x} $. بدلاً من اختيار فقط 3 أعمدة رقمية لإجراء التنبؤ، لماذا لا نستخدم جميع الأعمدة السبعة؟
cols = ['bias', 'cylinders', 'displacement', 'horsepower',
'weight', 'acceleration', 'model year', 'origin']
X = mpg_mat[cols].to_numpy()
mpg_mat[cols]
| origin | model year | acceleration | weight | horsepower | displacement | cylinders | bias | |
|---|---|---|---|---|---|---|---|---|
| 1 | 70 | 12 | 3504 | 130 | 307 | 8 | 1 | 0 |
| 1 | 70 | 11.5 | 3693 | 165 | 350 | 8 | 1 | 1 |
| 1 | 70 | 11 | 3436 | 150 | 318 | 8 | 1 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1 | 82 | 11.6 | 2295 | 84 | 135 | 4 | 1 | 389 |
| 1 | 82 | 18.6 | 2625 | 79 | 120 | 4 | 1 | 390 |
| 1 | 82 | 19.4 | 2720 | 82 | 119 | 4 | 1 | 391 |
392 rows × 8 columns
thetas_all = minimize(mse_loss, grad_mse_loss, X, y, progress=10)
print(f'theta: {thetas_all} | loss: {mse_loss(thetas_all, X, y):.2f}')
theta: [0. 0. 0. 0. 0. 0. 0. 0.] | loss: 610.47
theta: [-0.5 -0.81 0.02 -0.04 -0.01 -0.07 0.59 1.3 ] | loss: 11.22
theta: [-17.23 -0.49 0.02 -0.02 -0.01 0.08 0.75 1.43] | loss: 10.85
theta: [-17.22 -0.49 0.02 -0.02 -0.01 0.08 0.75 1.43] | loss: 10.85
وفقاً لنتيجة النزول الاشتقاقي، فإن النموذج الخطي يمكننا تعريفه كالتالي:
\[y = -17.22 - 0.49x_1 + 0.02x_2 - 0.02x_3 - 0.01x_4 + 0.08x_5 + 0.75x_6 + 1.43x_7\]نلاحظ أن خسارتنا قلت من 11.6 باستخدام ثلاث أعمدة إلى 10.85 باستخدام جميع الأعمدة الرقمية السبعة في بياناتنا. سنرى نسبة الخطأ في الرسم البياني لكل التوقعين السابق (باستخدام ثلاث أعمدة) والجديد (باستخدام سبع أعمدة):
resid_prop_all = (y - linear_model(thetas_all, X)) / with_predictions['mpg']
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.scatter(np.arange(len(resid_prop)), resid_prop, s=15)
plt.title('Residual proportions using 3 columns')
plt.xlabel('Index of row in data')
plt.ylabel('Error proportion')
plt.ylim(-0.7, 0.7)
plt.subplot(122)
plt.scatter(np.arange(len(resid_prop_all)), resid_prop_all, s=15)
plt.title('Residual proportions using 7 columns')
plt.xlabel('Index of row in data')
plt.ylabel('Error proportion')
plt.ylim(-0.7, 0.7)
plt.tight_layout();
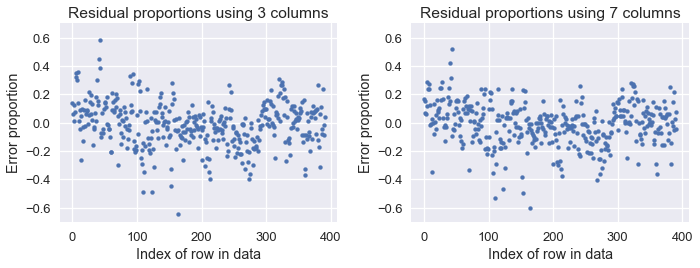
على الرغم أن الفرق بسيط، نلاحظ أن الفرق أقل عندما نستخدم السبع أعمدة. كلا النموذجين أفضل من النموذج الثابت، كما يوضح الرسم البياني التالي:
constant_resid_prop = (y - with_predictions['mpg'].mean()) / with_predictions['mpg']
plt.scatter(np.arange(len(constant_resid_prop)), constant_resid_prop, s=15)
plt.title('Residual proportions using constant model')
plt.xlabel('Index of row in data')
plt.ylabel('Error proportion')
plt.ylim(-1, 1);
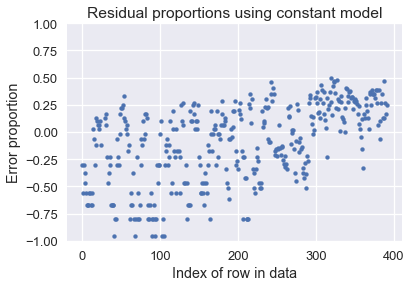
استخدام النموذج الثابت وصلت فيه نتائج الخطأ إلى أكثر من 75% لكثير من السيارات!
ملخص الانحدار الخطي المتعدد
تعرفنا على النموذج الخطي للانحدار. على عكس النموذج الثابت، الانحدار الخطي يأخذ خصائص من البيانات بالحسبان عند إجراء التوقعات، مما يجعله أكثر فائدة عندما يكون لدينا علاقات في بياناتنا.
خطوات ضبط النموذج من المفترض أن تكون واضحة الآن:
- اختيار النموذج.
- اختيار دالة الخسارة.
- تقليل دالة الخسارة باستخدام النزول الاشتقاقي.
من المفيد معرفة أن بإمكاننا التعديل على أحد المكونات دون الأخرى. في هذا الجزء، تعرفنا على النموذج الخطي دون التغير في دالة الخسارة أو استخدام خوارزميات تقليل أخرى. على الرغم أن النمذجة قد تكون معقدة، يكون أسهل التركيز على مكون واحد فقط في كل مرة، ثم جمع المكونات مع بعضها البعض.
المربعات الصغرى - منظور هندسي
لنتذكر أننا أوجدنا المتغيرات الرياضية المثالية للنموذج الخطي بواسطة التحسين من دالة الخسارة باستخدام النزول الاشتقاقي. ذكرنا أيضاً أن الانحدار الخطي للمربعات الصغرى يمكن حسابه تحليلياً. على الرغم أن النزول الاشتقاقي أكثر عملياً، هذا المنظور الهندسي سيساعدك على فهم الانحدار الخطي بشكل أكبر.
يتوقع من القارئ أن يكون على علم بفضاء المتجهات Vector Space وطريقة القيام بالعمليات الحسابية عليها.
لنفترض أننا نبحث عن النموذج الخطي للبيانات التالية:
| y | x |
|---|---|
| 2 | 3 |
| 1 | 0 |
| -2 | -1 |
data = pd.DataFrame(
[
[3,2],
[0,1],
[-1,-2]
],
columns=['x', 'y']
)
sns.regplot(x='x', y='y', data=data, ci=None, fit_reg=False);
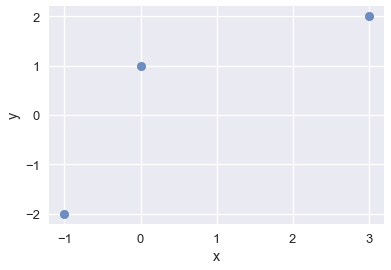
لنفترض أن النموذج المثالي هو النموذج بأقل خسارة، وان خطأ المربعات الصغرى هي أداة مقبولة للقياس.
المربعات الصغرى: النموذج الثابت
كما فعلنا في بيانات الإكراميات، لنبدأ بالنموذج الثابت: نموذج يتوقع رقم واحد فقط.
\[\theta = C\]نعمل نحن فقط مع قيم $ y $:
| y |
|---|
| 2 |
| 1 |
| -2 |
وهدفنا هو إيجاد قيمة $ \theta $ التي تنتج لنا خطاً يقلل من الخسارة التربيعية:
\[\begin{split} L(\theta, \textbf{y}) = \sum_{i = 1}^{n}(y_i - \theta)^2\\ \end{split}\]لنتذكر أن للنموذج الثابت، قيمة $ \theta $ التي تقلل الخسارة في دالة الخطأ التربيعي المتوسط MSE هي $ \bar{\textbf{y}} $، متوسط قيم $ \textbf{y} $. يمكن إيجاد العملية الحسابية الكاملة في جزء دوال الخسارة في فصل النماذج والتوقعات.
لاحظ أن دالة الخسارة لدينا هي مجمع التربيع. القاعدة L2 للمتجهات هي أيضاً مجموع التربيع، ولكن مع الجذر التربيعي:
\[\Vert \textbf{v} \Vert = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2}\]إذا جعلنا $ y_i - \theta = v_i $:
\[\begin{split} \begin{aligned} L(\theta, \textbf{y}) &= v_1^2 + v_2^2 + \dots + v_n^2 \\ &= \Vert \textbf{v} \Vert^2 \end{aligned} \end{split}\]يعني ذلك أن بإمكاننا تعريف الخسارة على أنها تربيع القاعدة L2 لمتّجه $ \textbf{v} $. يمكننا وصف $ v_i $ كالتالي $ y_i - \theta \quad \forall i \in [1,n] $ إذاً ذلك في كتعريف ديكارتي:
\[\begin{split} \begin{aligned} \textbf{v} \quad &= \quad \begin{bmatrix} y_1 - \theta \\ y_2 - \theta \\ \vdots \\ y_n - \theta \end{bmatrix} \\ &= \quad \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \quad - \quad \begin{bmatrix} \theta \\ \theta \\ \vdots \\ \theta \end{bmatrix} \\ &= \quad \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \quad - \quad \theta \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix} \end{aligned} \end{split}\]إذاً، يمكننا كتابة دالة الخسارة كالتالي:
\[\begin{split} \begin{aligned} L(\theta, \textbf{y}) \quad &= \quad \left \Vert \qquad \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \quad - \quad \theta \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix} \qquad \right \Vert ^2 \\ \quad &= \quad \left \Vert \qquad \textbf{y} \quad - \quad \hat{\textbf{y}} \qquad \right \Vert ^2 \\ \end{aligned} \end{split}\]الوصف \(\theta \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}\) هو مضاعف عددي للأعمدة في المتّجه $ \textbf{1} $، وهي أيضاً نتيجة التوقع، ويرمز لها $ \hat{\textbf{y}} $.
يعطينا ذلك منظوراً جديداً عن معنى تقليل الخسارة في خطأ المربعات الصغرى.
قيم $ \textbf{y} $ و $ \textbf{1} $ ثابتة، ولكن $ \theta $ يمكن أن تأخذ أي قيمة، لذا $ \hat{\textbf{y}} $ يمكن أن تكون أي مضاعف عددي ل $ \textbf{1} $. نريد إيجاد $ \theta $ لتكون $ \theta \textbf{1} $ أقرب ما تكون إلى $ \textbf{y} $. نستخدم $ \hat{\theta} $ لوصف ذلك الضبط المثالي ل $ \theta $.
المربعات الصغرى: نموذج خطي بسيط
الآن، لنلقي نظره على نموذج الانحدار الخطي البسيط. يشبه النموذج بشكل كبير لاشتقاق النموذج الثابت، ولكن لاحظ الفرق وفكر بطريقة عامة لإجراء الانحدار الخطي المتعدد.
النموذج الخطي البسيط هو:
\[\begin{split} \begin{aligned} f_\boldsymbol\theta (x_i) &= \theta_0 + \theta_1 x_i \\ \end{aligned} \end{split}\]هدفنا إيجاد $ \boldsymbol\theta $ التي تنتج لنا خطاً بأقل خطأ تربيعي:
\[\begin{split} \begin{aligned} L(\boldsymbol\theta, \textbf{x}, \textbf{y}) &= \sum_{i = 1}^{n}(y_i - f_\boldsymbol\theta (x_i))^2\\ &= \sum_{i = 1}^{n}(y_i - \theta_0 - \theta_1 x_i)^2\\ &= \sum_{i = 1}^{n}(y_i - \begin{bmatrix} 1 & x_i \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix} ) ^2 \end{aligned} \end{split}\]لمساعدتنا على تحويل شكل جمع الخسارة إلى شكل مصفوفة، دعنا نوسع من الخسارة ب $ n = 3 $:
\[\begin{split} \begin{aligned} L(\boldsymbol{\theta}, \textbf{x}, \textbf{y}) &= (y_1 - \begin{bmatrix} 1 & x_1 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix})^2 \\ &+ (y_2 - \begin{bmatrix} 1 & x_2 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix})^2 \\ &+ (y_3 - \begin{bmatrix} 1 & x_3 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix})^2 \\ \end{aligned} \end{split}\]مرة أخرى، دالة الخسارة هي مجموع التربيع و القاعدة L2 للمتّجه هي الجذر التربيعي لمجموع التربيع:
\[\Vert \textbf{v} \Vert = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2}\]إذا جعلنا \(y_i - \begin{bmatrix} 1 & x_i \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix}\) $ v_i = $:
\[\begin{split} \begin{aligned} L(\boldsymbol{\theta}, \textbf{x}, \textbf{y}) &= v_1^2 + v_2^2 + \dots + v_n^2 \\ &= \Vert \textbf{v} \Vert^2 \end{aligned} \end{split}\]كما في السابق، يمكننا وصف خسارتنا على أنها تربيع القاعدة L2 للمتّجه $ \textbf{v} $.
\[v_i = y_i - \begin{bmatrix} 1 & x_i \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix} \quad \forall i \in [1,3]\] \[\begin{aligned} L(\boldsymbol{\theta}, \textbf{x}, \textbf{y}) &= \left \Vert \qquad \begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix} \quad - \quad \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix} \qquad \right \Vert ^2 \\ &= \left \Vert \qquad \textbf{y} \quad - \quad \textbf{X} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix} \qquad \right \Vert ^2 \\ &= \left \Vert \qquad \textbf{y} \quad - \quad f_\boldsymbol\theta(\textbf{x}) \qquad \right \Vert ^2 \\ &= \left \Vert \qquad \textbf{y} \quad - \quad \hat{\textbf{y}} \qquad \right \Vert ^2 \\ \end{aligned}\]عملية ضرب المصفوفة \(\begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \end{bmatrix}\) هي تركيبة خطية للأعمدة في $ \textbf{X} $: كل $ \theta_i $ يتم ضربها بعمود واحد من $ \textbf{X} $، يظهر لنا هذا المنظور أن $ f_\boldsymbol\theta $ تركيبة خطية للخصائص في بياناتنا.
$ \textbf{X} $ و $ \textbf{y} $ ثابتين، ولكن $ \theta_0 $ و $ \theta_1 $ يمكن أن يأخذان أي قيمه، لذا $ \hat{\textbf{y}} $ يمكن أن تأخذ أياً من التركيبات الخطية من الأعمدة في $ \textbf{X} $. للحصول على أقل خسارة، تريد أن نختار $ \boldsymbol\theta $ التي فيها $ \hat{\textbf{y}} $ أقرب ما تكون إلى $ \textbf{y} $، يرمز لها بالرمز $ \hat{\boldsymbol\theta} $.
الفكرة الهندسية
الآن، لنحاول تكوين فكرة عن أهمية أن تكون $ \hat{\textbf{y}} $ محدودة للتركيبات الخطية للأعمدة في $ \textbf{X} $. على الرغم أن مدى أي متّجه يحتوي على عدد غير محدود من التركيبات الخطية، غير محدود لا تعني أياً كان، التركيبات الخطية محدودة بواسطة أساس المتّجه.
للتذكير، هذه دالة الخسارة ومخطط التشتت:
\[L(\boldsymbol{\theta}, \textbf{x}, \textbf{y}) \quad = \quad \left \Vert \quad \textbf{y} \quad - \quad \textbf{X} \boldsymbol\theta \quad \right \Vert ^2\]sns.regplot(x='x', y='y', data=data, ci=None, fit_reg=False);
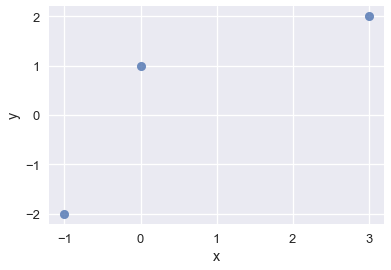
من خلال مشاهدتنا لمخطط التشتت، نلاحظ أنه لا يوجد خط مثالي للنقاط، لذا لن نستطيع الوصول إلى خسارة تساوي صفر. نعرف أن $ \textbf{y} $ ليست على مستوى خطي مع $ \textbf{x} $ و $ \textbf{1}:
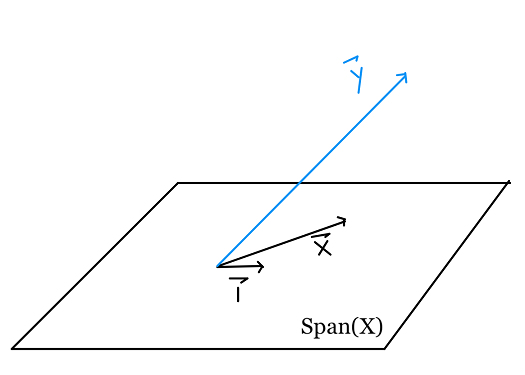
بما أن حساب الخسارة يكون بالمسافة، يمكننا ملاحظة أنه لتقليل الخسارة $ L(\boldsymbol\theta, \textbf{x}, \textbf{y}) = \left \Vert \textbf{y} - \textbf{X} \boldsymbol\theta \right \Vert ^2 $، فنريد أن تكون $ \textbf{X} \boldsymbol\theta $ أقرب ما تكون إلى $ \textbf{y} $.
رياضياً، نرى توقع $ \textbf{y} $ في فضاء المتّجه الممتد بواسطة الأعمدة في $ \textbf{X} $، لأن التوقع لأي متّجه هي أقرب نقطة في $ Span(\textbf{X})$ للمتّجه. لذا، اختيار $ \boldsymbol\theta $ يكون فيها $ \hat{\textbf{y}} $ $ \textbf{X} \boldsymbol\theta = $ $ \mathit{proj}_{Span(\textbf{X})} \textbf{y} = $ هو الحل المثالي.
proj = projection = التوقع
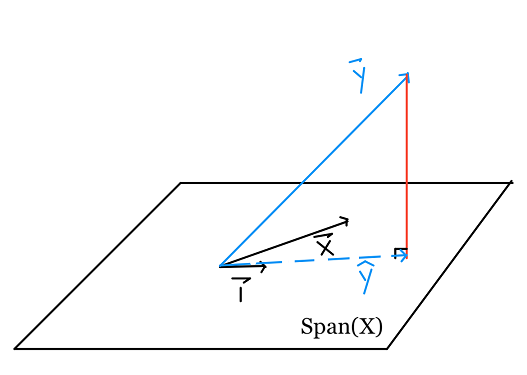
لنعرف لماذا، لنأخذ بالاعتبار النقاط الأخرى في فضاء المتّجه، النقاط باللون البنفسجي:
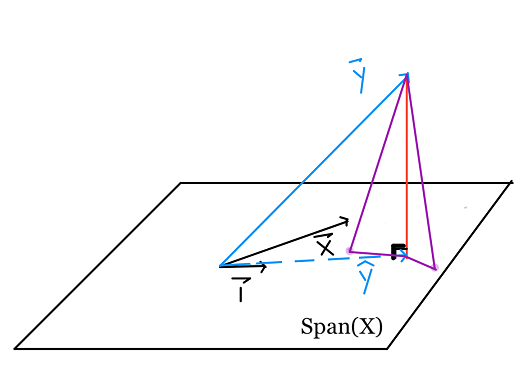
بناءًا على نظرية فيثاغورس، أي نقطة على السطح هي أبعد عن $ \textbf{y} $ من $ \hat{\textbf{y}} $. طول العمود المقابل ل $ \hat{\textbf{y}} $ هو خطأ المربعات الصغرى.
الجبر الخطي
تحدثنا بشكل كبير عن الجبر الخطي، ما تبقى لنا الآن هو حل $ \hat{\boldsymbol\theta} $ التي تكون لنا ما نبحث عنه $ \hat{\textbf{y}} $
بعض النقاط نأخذها بالاعتبار:
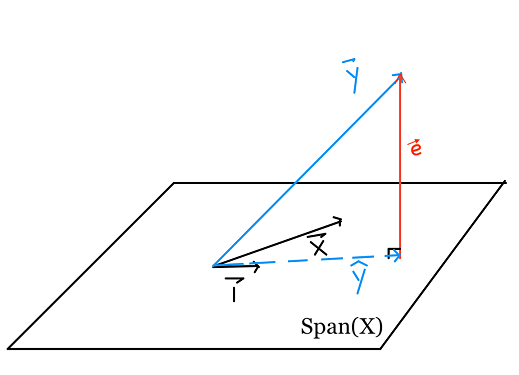
- $ \hat{\textbf{y}} + \textbf{e} = \textbf{y} $
- $ \textbf{e} $ متوازيه عامودياً مع $ \textbf{x} $ و $ \textbf{1} $
- $ \hat{\textbf{y}} = \textbf{X} \hat{\boldsymbol\theta} $ هي المتّجه الأقرب إلى $ \textbf{y} $ في فضاء المتّجهات الممتدة من $ \textbf{x} $ و $ \textbf{1} $
ولذا، تنتج لنا المعادلة التالية:
\[\textbf{X} \hat{\boldsymbol\theta} + \textbf{e} = \textbf{y}\]ضرب الجهة اليسرى لكل القيم ب $ \textbf{X}^T $ ينتج لنا التالي:
\[\textbf{X}^T \textbf{X} \hat{\boldsymbol\theta} + \textbf{X}^T \textbf{e} = \textbf{X}^T \textbf{y}\]بما أن $ \textbf{e} $ متعامدة مع الأعمدة في $ \textbf{X} $، فإن $ \textbf{X}^T \textbf{e} $ هو عمود متّجه يحتوي على أصفار. لذا، نصل إلى المعادلة التالية:
\[\textbf{X}^T \textbf{X} \hat{\boldsymbol\theta} = \textbf{X}^T \textbf{y}\]من هنا، يمكننا بسهولة الحل لإيجاد $ \hat{\boldsymbol\theta} $ بواسطة ضرب الجهة اليسرى في كلا الجانبين ب $ (\textbf{X}^T \textbf{X})^{-1} $:
\[\hat{\boldsymbol\theta} = (\textbf{X}^T \textbf{X})^{-1} \textbf{X}^T \textbf{y}\]ملاحظة: يمكننا الحصول على نفس النتيجة بواسطة التقليل باستخدام متجهات التفاضل والتكامل، ولكن بالنسبة لخطأ المربعات الصغرى، متجهات التفاضل والتكامل ليست ضرورية. لدوال الخسارة الأخرى، سنحتاج لاستخدام متجهات التفاضل والتكامل للحصول على النتيجة التحليلية.
إنهاء الدراسة
لنعود لتجربتنا، لنطبق ما تعلمناه، ونشرح إجابتنا:
\[\begin{split} \textbf{y} = \begin{bmatrix} 2 \\ 1 \\ -2 \end{bmatrix} \qquad \textbf{X} = \begin{bmatrix} 1 & 3 \\ 1 & 0 \\ 1 & -1 \end{bmatrix} \end{split}\] \[\begin{split} \begin{align} \hat{\boldsymbol\theta} &= \left( \begin{bmatrix} 1 & 1 & 1 \\ 3 & 0 & -1 \end{bmatrix} \begin{bmatrix} 1 & 3 \\ 1 & 0 \\ 1 & -1 \end{bmatrix} \right)^{-1} \begin{bmatrix} 1 & 1 & 1 \\ 3 & 0 & -1 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ -2 \end{bmatrix} \\ &= \left( \begin{bmatrix} 3 & 2\\ 2 & 10 \end{bmatrix} \right)^{-1} \begin{bmatrix} 1 \\ 8 \end{bmatrix} \\ &= \frac{1}{30-4} \begin{bmatrix} 10 & -2\\ -2 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 8 \end{bmatrix} \\ &= \frac{1}{26} \begin{bmatrix} -6 \\ 22 \end{bmatrix}\\ &= \begin{bmatrix} - \frac{3}{13} \\ \frac{11}{13} \end{bmatrix} \end{align} \end{split}\]قمنا تحليلياً بإيجاد النموذج المثالي لانحدار المربعات الصغرى وهو $ f_\boldsymbol{\boldsymbol\theta}(x_i) = - \frac{3}{13} + \frac{11}{13} x_i $. نعرف أن اختيارنا ل $ \boldsymbol\theta $ صحيح باستخدام الخاصية الرياضية التي تقول توقع $ \textbf{y} $ لامتداد الأعمدة في $ \textbf{X} $ ينتج لنا أقرب نقطة في فضاء المتّجه ل $ \textbf{y} $. تحت القيود الخطية باستخدام خسارة المربعات الصغرى، الحل ل $ \hat{\boldsymbol\theta} $ ينتج لنا توقع مضمون أنه الحل الأفضل.
عندما تعتمد المتغيرات خطياً
لكل متغير إضافي، نضيف عممود جديد إلى $ \textbf{X} $. امتداد أعمدة ل $ \textbf{X} $ هو التركيب الخطي لأعمدة المتّجهات، لذا إضافة أعمدة تغير من الامتداد فقط إذا كانت مستقلة خطياً عن بقية الأعمدة الموجودة مسبقاً.
عندما يكون العمود المضاف غير مستقل خطياً، يمكن وصفة كتركيب خطي من أحد الأعمدة الأخرى، لذا، لن يكون لنا أي متّجه جديده في الفضاء الجزئي.
لنتذكر أن امتداد $ \textbf{X} $ مهم لأنه الفضاء الجزئي الذي نريد أن نتوقع $ \textbf{y} $ فيه. إذا لم يتغير هذا الفضاء، فإن التوقع لن يتغير.
مثلاً، عندما عرفنا $ \textbf{x} $ على النموذج الثابت لنحصل على النموذج الخطي البسيط، عرفنا دالة مستقلة. \(\textbf{x} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix}\) لا يمكن وصفها كعدديه من \(\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\). لذا، انتقلنا من إيجاد توقع ل $ \textbf{y} $ في الخط:
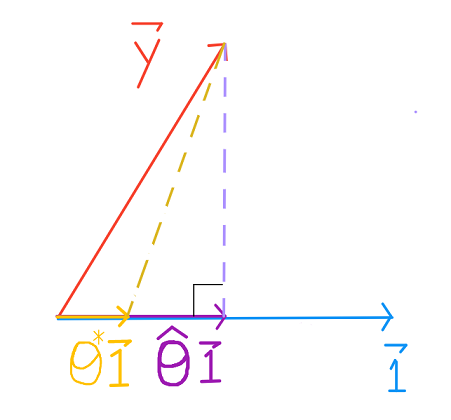
إلى إيجاد توقع ل $ \textbf{y} $ على السطح:

الآن، لنعرف متغير آخر، $ \textbf{z} $، يكون بشكل واضح هذا العمود متحيز:
| y | x | 1 | z |
|---|---|---|---|
| 2 | 3 | 1 | 4 |
| 1 | 0 | 1 | 1 |
| -2 | -1 | 1 | 0 |
لاحظ أن $ \textbf{z} = \textbf{1} + \textbf{x} $. بما أن $ \textbf{z} $ تركيبتها خطية من $ \textbf{1} $ و $ \textbf{x} $، فأنها تقع في $ Span(\textbf{X}) $. الآن، $ \textbf{z} $ معتمده خطياً على $ \{\textbf{1} ,\textbf{x}\} $ ولا تغيّر في $ Span(\textbf{X}) $. لذا، توقع $ \textbf{y} $ في الفضاء الجزئي الممتد بواسطة $ \textbf{1} $، $ \textbf{x} $ و $ \textbf{z} $ سيكون مطابق لتوقع $ \textbf{y} $ في الفضاء الجزئي الممتد بواسطة $ \textbf{1} $ و $ \textbf{x} $.
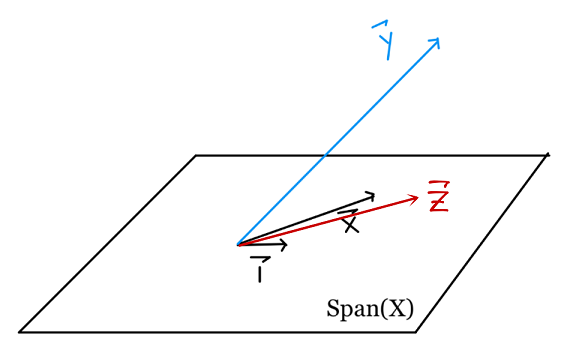
يمكننا ايضاً ملاحظة ذلك عند تقليل دالة الخسارة:
\[\begin{split} \begin{aligned} L(\boldsymbol\theta, \textbf{d}, \textbf{y}) &= \left \Vert \qquad \begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix} \quad - \quad \begin{bmatrix} 1 & x_1 & z_1 \\ 1 & x_2 & z_2\\ 1 & x_3 & z_3\end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix} \qquad \right \Vert ^2 \end{aligned} \end{split}\]الحل المتوقع لنا سيكون كالشكل التالي $ \theta_0 \textbf{1} + \theta_1 \textbf{x} + \theta_2 \textbf{z} $.
بما أن $ \textbf{z} = \textbf{1} + \textbf{x} $، ايضاً كانت $ \theta_0 $، $ \theta_1 $ و $ \theta_2 $، القيم المتوقعة يمكن إعادة كتابتها كالتالي:
\[\begin{split} \begin{aligned} \theta_0 \textbf{1} + \theta_1 \textbf{x} + \theta_2 (\textbf{1} + \textbf{x}) &= (\theta_0 + \theta_2) \textbf{1} + (\theta_1 + \theta_2) \textbf{x} \\ \end{aligned} \end{split}\]إذاً، إضافة $ \textbf{z} $ لن تغير أي شيء. الفرق الوحيد هو أن بإمكاننا وصف هذا التوقع بعدة أشكال. لنتذكر أننا أوجدنا توقع $ \textbf{y} $ على امتداد $ \textbf{1} $ و $ \textbf{x} $ وكان:
\[\begin{split} \begin{bmatrix} \textbf{1} & \textbf{x} \end{bmatrix} \begin{bmatrix} - \frac{3}{13} \\ \frac{11}{13} \end{bmatrix} = - \frac{3}{13} \textbf{1} + \frac{11}{13} \textbf{x}\end{split}\]لكن، مع التعرف على $ \textbf{z} $، يمكننا وصف توقع المتّجه بأكثر من طريقه.
بما أن $ \textbf{1} = \textbf{z} - \textbf{x} $، ف $ \hat{\textbf{y}} $ يمكن وصفها كالتالي:
\[- \frac{3}{13} (\textbf{z} - \textbf{x}) + \frac{11}{13} \textbf{x} = - \frac{3}{13} \textbf{z} + \frac{14}{13} \textbf{x}\]بما أن $ \textbf{x} = \textbf{z} + \textbf{1} $، ف $ \hat{\textbf{y}} $ يمكن وصفها كالتالي:
\[- \frac{3}{13} \textbf{1} + \frac{11}{13} (\textbf{z} + \textbf{1}) = \frac{8}{13} \textbf{1} + \frac{11}{13} \textbf{z}\]ولكن جميع الأوصاف الثلاثة تقدم نفس التوقع.
في الختام، إضافة عمود غير مستقل خطياً إلى $ \textbf{x} $ لا يغير في $ Span(\textbf{X}) $، ولذلك لن يغير في التوقع والحل لمشكلة المربعات الصغرى.
طريقتين للتفكير
أضفنا مخططات التشتت مرتين في هذا الدرس. أول مرة للتذكير أنه كما في السابق، نحاول إيجاد الخط المثالي للبيانات. المرة الثانية كانت تأكد أنه لا يوجد خط مثالي لجميع النقاط. بصرف النظر هن ذلك، حاولنا عدم تخريب رسم فضاء المتّجه بمخططات التشتت. ذلك لأن مخططات التشتت تتوافق مع نظرية مساحة الصف في مشكلة المربعات الصغرى: النظر لكل نقاط البيانات ومحاولة التقليل في المسافة بين توقعنا و كل نقطة. في هذا الدرس، تعرفنا على نطريقة مساحة العامود: كل متغير كان متّجه، تكون لنا فضاء من الإجابات المُحتملة (التوقعات).
تطبيق عملي للانحدار الخطي
في هذا الجزء، سنقوم بتطبيق عملي لنموذج الانحدار الخطي على بيانات. لدى البيانات التي سنعمل عليها العديد من الخصائص، مثل الطول والحجم لحيوان الحِمار.
مهمتنا هي توقع الوزن باستخدام الانحدار الخطي.
نظره عامه على البيانات
سنبدأ أولاً بقراءة البيانات وأخذ نظره سريعة على محتواها:
لتحميل البيانات، اضغط هنا.
import pandas as pd
donkeys = pd.read_csv("donkeys.csv")
donkeys.head()
| WeightAlt | Weight | Height | … | Sex | Age | BCS | |
|---|---|---|---|---|---|---|---|
| NaN | 77 | 90 | … | stallion | 2> | 3 | 0 |
| NaN | 100 | 94 | … | stallion | 2> | 2.5 | 1 |
| NaN | 74 | 95 | … | stallion | 2> | 1.5 | 2 |
| NaN | 116 | 96 | … | female | 2> | 3 | 3 |
| NaN | 91 | 91 | … | female | 2> | 2.5 | 4 |
5 rows × 8 columns
فكرة جيدة دائماً هي النظر لعدد البيانات لدينا عن طريق عرض مقاسات الـ DataFrame. عندما يكون حجم البيانات لدينا كبير، طباعة كامل البيانات قد يسبب مشاكل للمتصفح وتتسبب بإغلاقه:
donkeys.shape
(544, 8)
البيانات قليله نسبياً، لدينا فقط 544 سطر و 8 أعمدة. لنرى ما هي الأعمدة المتوفرة لدينا:
donkeys.columns.values
array(['BCS', 'Age', 'Sex', 'Length', 'Girth', 'Height', 'Weight',
'WeightAlt'], dtype=object)
فهم البيانات لدينا يساعدنا على توجيه عملية تحليلنا لها، يجب علينا فهم ما يحتويه كل عمود. بعض هذه الأعمدة واضحة من مسمياتها، ولكن بعضها يحتاج شرحاً أكثر:
BCS(Body Condition Score): حالة الجسم (تقييم لصحة جسد الحيوان).Grith: مقياس لمتوسط جسم الحيوان.WeightAlt: وزن آخر (من بين البيانات لدينا تم وزن بعضهم مرتين وعددهم 31، تم وزنهم مرتين للتأكد من دقة الوزن).
فكرة مناسبة الآن هو تحديد أي الأعمدة تحتوي على بيانات كمية وأيها يحتوي على بيانات أسميه.
الكمية: Length، Girth، Height، Weight و WeightAlt.
الاسمية: BCS، Age و Sex.
تنظيف البيانات
في هذا الجزء، سنتحقق من البيانات إذا كانت تحتوي على أي شذوذ ونتعامل معها.
عن طريق التحقق من عمود WeightAlt، يمكننا التأكد من دقة الوزن بأخذ الفرق بين الوزنين ورسمها النتائج:
difference = donkeys['WeightAlt'] - donkeys['Weight']
sns.distplot(difference.dropna());
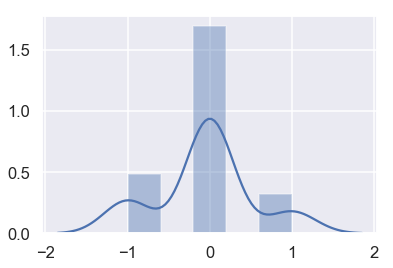
الأوزان تبدو معقولة بفارق 1 أو أقل كيلو قرام فيما بينها.
الآن، يمكننا النظر إلى قيم غريبه والتي قد تظر أن لدينا مشاكل أو أخطاء. يمكننا استخدام الدالة Quantile للكشف عن القيم الشاذه:
donkeys.quantile([0.005, 0.995])
| WeightAlt | Weight | Height | Girth | Length | BCS | |
|---|---|---|---|---|---|---|
| 98.75 | 71.715 | 89 | 90 | 71.145 | 1.5 | 0.005 |
| 192.8 | 214 | 112 | 131.285 | 111 | 4 | 0.995 |
شرح مبسط للدالة quantile:
تقوم الدالة بإظهار نتائج بناءًا على النسبة المعطاة لها، في المثال السابق طلبنا نتائج من هم في النسبة 0.005 وأقل و منهم في النسبة 0.995 وأقل.
مثلاً في العمود Height، يظهر لنا أن 0.5% أو أقل يبلغ طولهم 89.0 بينما 99.5% أو أقل يبلغ طولهم 112.0 في بياناتنا.
لكل الأعمدة الكمية، يمكن أن نبحث عن أي سطر تكون نتيجته خارج هذه الأعداد، لأننا نريد أن يطبق النموذج على أي حيوان صحته ممتازة وناضح.
أولاً، لنرى العمود BCS:
donkeys[(donkeys['BCS'] < 1.5) | (donkeys['BCS'] > 4)]['BCS']
291 4.5
445 1.0
Name: BCS, dtype: float64
أيضاً عند النظر على المخطط الشريطي للعمود BCS:
plt.hist(donkeys['BCS'], density=True)
plt.xlabel('BCS');
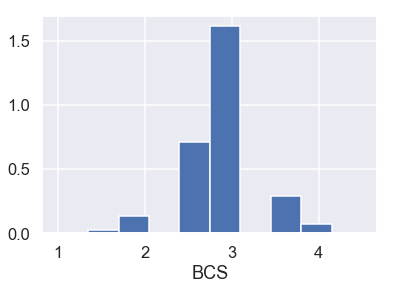
بالأخذ بالإعتبار أن العمود BCS يظهر لنا مدى صحة ونضوج الحيوان، حصول الحيوان على 1 يبين أنه هزيل وحصوله على 4.5 يبين أن وزنه زائد. أيضاً بالنظر إلى المخطط الشريطي، فقط يظهر لدينا اثنين بقيم شاذه في العمود BCS. لذا سنقوم بحذف هذه البيانات.
الآن، لنلقي نظره على الأعمدة Length، Girth و Height:
donkeys[(donkeys['Length'] < 71.145) | (donkeys['Length'] > 111)]['Length']
8 46
22 68
26 69
216 112
Name: Length, dtype: int64
donkeys[(donkeys['Girth'] < 90) | (donkeys['Girth'] > 131.285)]['Girth']
8 66
239 132
283 134
523 134
Name: Girth, dtype: int64
donkeys[(donkeys['Height'] < 89) | (donkeys['Height'] > 112)]['Height']
8 71
22 86
244 113
523 116
Name: Height, dtype: int64
بالنسبة لهذه الأعمدة الثلاثة، يبدو أن السطر 8 يحتوي على قيم ادنى من باقي البيانات بينما الأسطر الأخرى قريبه جداً من باقي البيانات ولا يحتاج أن نحذفها.
أخيراً، لنرى العمود Weight:
donkeys[(donkeys['Weight'] < 71.715) | (donkeys['Weight'] > 214)]['Weight']
8 27
26 65
50 71
291 227
523 230
Name: Weight, dtype: int64
أو سطرين وآخر سطرين بعيدة جداً عن بقية البيانات وعلى الأرجح سنقوم بحذفها. يمكننا أن نبقي السطر في المنتصف كونه قريباً جداً من بقية البيانات.
بما أن العمود WeightAlt مشابه للعمود Weight، لن نقوم بالبحث عن شواذ فيه. ولتجميع ما فهمناه، هذا ما سنقوم بفلترته في بياناتنا:
- الإبقاء على البيانات بين 1.5 و 4 في العمود
BCS. - الإبقاء على الأسطر التي بياناتها بين 71 و 214 في العمود
Weight.
donkeys_c = donkeys[(donkeys['BCS'] >= 1.5) & (donkeys['BCS'] <= 4) &
(donkeys['Weight'] >= 71) & (donkeys['Weight'] <= 214)]
فصل بيانات التدريب والاختبار
قبل أن نبدأ بتحليل البيانات، نريد أن نقسم البيانات إلى تقسيم 80/20، نستخدم فيها 80% من البيانات لتدريب النموذج، ونترك 20% لتقييم واختبار النموذج:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(donkeys_c.drop(['Weight'], axis=1),
donkeys_c['Weight'],
test_size=0.2,
random_state=42)
X_train.shape, X_test.shape
((431, 7), (108, 7))
أستخدم الكاتب دالة train_test_split والتي تأتي من مكتبة sklearn وهي مكتبة متخصصه بأدوات تحليل البيانات وتعلم الآله.
نقوم أيضاً بإنشاء دالة تقييم التوقع على بيانات الإختبار، لنستخدم الخطأ التربيعي المتوسط:
def mse_test_set(predictions):
return float(np.sum((predictions - y_test) ** 2))
استكشاف البيانات وتصويرها
كالمعتاد، سنتحقق من البيانات قبل محاولة ضبط النموذج عليها.
أولاً، لنطلع على البيانات الاسمية باستخدام مخطط الصندوق:
sns.boxplot(x=X_train['BCS'], y=y_train);
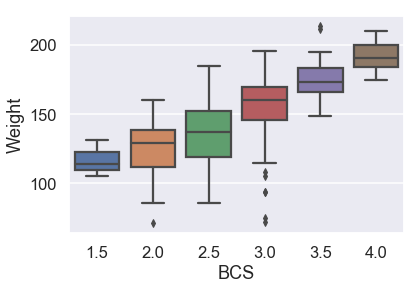
يبدو أن متوسط الوزن يزداد مع BCS، وليس خطياً:
sns.boxplot(x=X_train['Sex'], y=y_train,
order = ['female', 'stallion', 'gelding']);
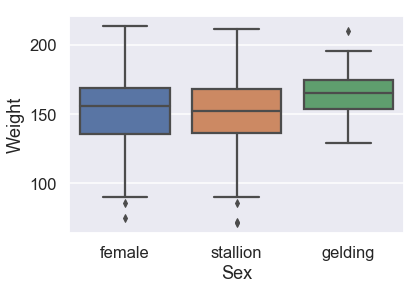
يظهر أن الجنس لا يتأثر كثيراً بالوزن
sns.boxplot(x=X_train['Age'], y=y_train,
order = ['<2', '2-5', '5-10', '10-15', '15-20', '>20']);
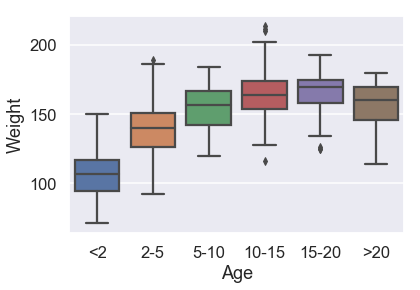
بعمر 5 أو أكثر، توزيع الأوزان لا يظهر أي تغير كبير.
الآن، لنلقي نظره على البيانات الكمية. يمكننا رسم كل واحدٍ منها مع المتغير الذي نريد التنبؤ عنه:
X_train['Weight'] = y_train
sns.regplot('Length', 'Weight', X_train, fit_reg=False);
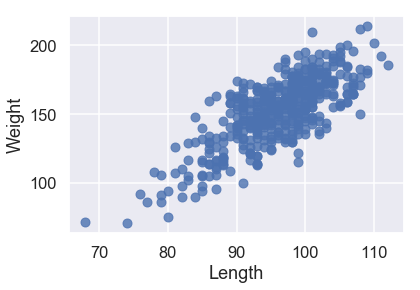
sns.regplot('Girth', 'Weight', X_train, fit_reg=False);
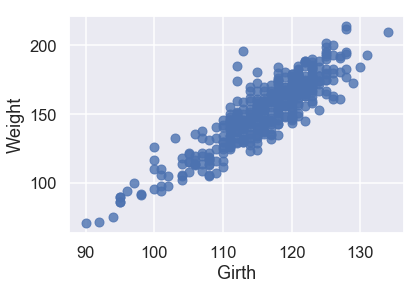
sns.regplot('Height', 'Weight', X_train, fit_reg=False);
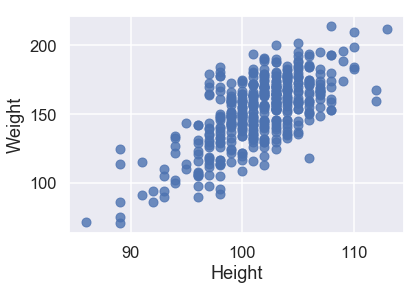
جميع البيانات الكمية لديها علاقة خطية مع المتغير الذي نريد توقعه Weight، لذا لا نحتاج للقيام بأي تعديلات على البيانات التي سندرب النموذج عليها.
أيضاً تبدو فكرة جيدة إذا رأينا بين كل متغير وآخر إذا كانت العلاقة بينهم خطية. سنقوم برسم اثنين:
sns.regplot('Height', 'Length', X_train, fit_reg=False);
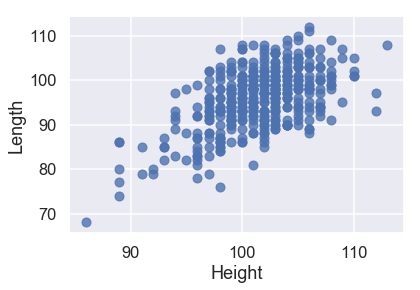
sns.regplot('Height', 'Girth', X_train, fit_reg=False);
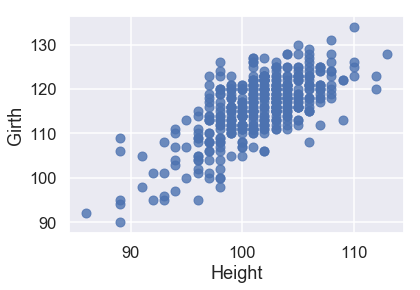
من هذه الرسوم، نلاحظ أيضاً أن المتغيرات التي تساعدنا على التنبؤ لديها علاقة خطية قوية فيما بينها. يصعب ذلك من عملية تفسير نتائج النموذج، لذا لنتذكر لذلك بعد إنشاء النموذج.
نماذج خطية أبسط
بدلاً من استخدام كل البيانات مرة واحدة، لنجرب ضبط النموذج على متغير أو اثنين أولاً.
في الأسفل ثلاث نماذج انحدار خطي فقط باستخدام متغير كمي واحد. أي هذه النماذج يبدو الأفضل؟
sns.regplot('Length', 'Weight', X_train, fit_reg=True);
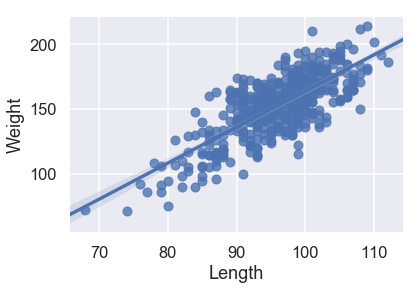
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train[['Length']], X_train['Weight'])
predictions = model.predict(X_test[['Length']])
print("MSE:", mse_test_set(predictions))
MSE: 26052.58007702549
sns.regplot('Girth', 'Weight', X_train, fit_reg=True);
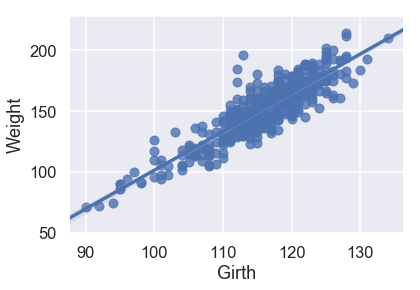
model = LinearRegression()
model.fit(X_train[['Girth']], X_train['Weight'])
predictions = model.predict(X_test[['Girth']])
print("MSE:", mse_test_set(predictions))
MSE: 13248.814105932383
sns.regplot('Height', 'Weight', X_train, fit_reg=True);
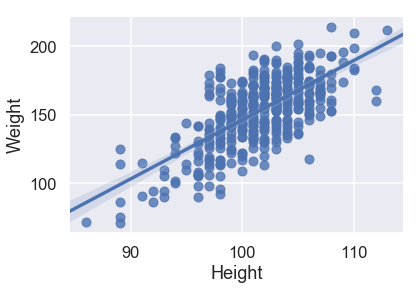
model = LinearRegression()
model.fit(X_train[['Height']], X_train['Weight'])
predictions = model.predict(X_test[['Height']])
print("MSE:", mse_test_set(predictions))
MSE: 36343.308584306134
بالنظر إلى مهطط التشتت ونتيجة MSE، يبدو لنا أن Girth هي الأفضل لتوقع الوزن وحدها كون لديها علاقة خطية قوية مع Weight ولديها أقل قيمة للخطأ التربيعي المتوسط.
هل سنحصل على أداء أفضل عند استخدام مُتغيرين؟ لنجرب ضبط النموذج باستخدام Girth و Length. على الرغم انه من الصعب رسم هذا النموذج، يمكننا رؤية نتيجة الخطأ التربيعي المتوسط:
model = LinearRegression()
model.fit(X_train[['Girth', 'Length']], X_train['Weight'])
predictions = model.predict(X_test[['Girth', 'Length']])
print("MSE:", mse_test_set(predictions))
MSE: 9680.902423377258
رائع! يبدو أن MSE تم تقليلها لدينا من حوالي 13000 باستخدام Girth وحدها إلى 10000 باستخدام Girth و Length. أضافة متغير أخر حسن من نموذجنا.
يمكننا أيضاً استخدام المتغيرات الاسمية في نموذجنا. لنرى الآن كيف نستخدم النموذج الخطي مع البيانات الاسمية في العمود Age. هذا الرسم البياني ل Age و Weight:
sns.stripplot(x='Age', y='Weight', data=X_train, order=['<2', '2-5', '5-10', '10-15', '15-20', '>20']);
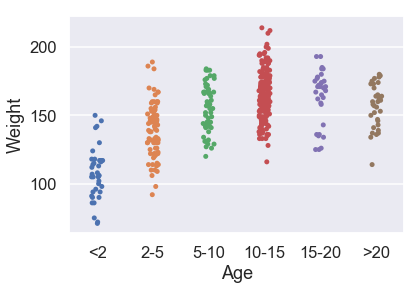
بما أن البيانات في العمود Age أسميه، فنحتاج لاستخدام بيانات رقمية مطابقة لها لنتمكن من تطبيق نموذج الانحدار الخطي عليه:
just_age_and_weight = X_train[['Age', 'Weight']]
with_age_dummies = pd.get_dummies(just_age_and_weight, columns=['Age'])
model = LinearRegression()
model.fit(with_age_dummies.drop('Weight', axis=1), with_age_dummies['Weight'])
just_age_and_weight_test = X_test[['Age']]
with_age_dummies_test = pd.get_dummies(just_age_and_weight_test, columns=['Age'])
predictions = model.predict(with_age_dummies_test)
print("MSE:", mse_test_set(predictions))
MSE: 41398.515625
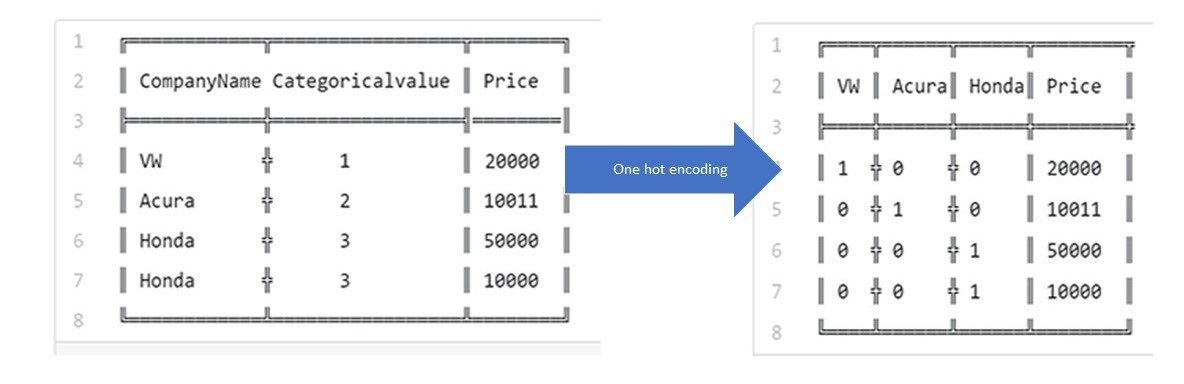
استخدم الكاتب الدالة
get_dummiesلتحويل المتغيرات الاسمية إلى بيانات وهمية كمية تتكون من 0 و 1، يطلق على هذه الطريقة ب One-hot encoding ويمكن وصفها في الصورة التالية:
نتيجة 40000 أسولأ بكثير مما حصلنا عليه باستخدام متغير كمي واحد، ولكن هذا المتغير قد يثبت أهميته في نموذجنا الخطي.
لنحاول تفسير هذا النموذج. لاحظ أن أي حِمار عمره لنقل بين 2 و 5 سنوات، سيحصل على نفس التوقع لأن لديهم نفس المدخلات: 1 للعمود إلى يحدد العمر بين 2-5 سنوات. و 0 في بقية الأعمدة. لذا، يمكننا تفسير المتغيرات الاسمية ببساطه بتغير القيم في النموذج لأن المتغيرات الاسمية تفصلهم إلى مجموعات وتعطي توقع واحد لجميع من في هذه المجموعة.
خطوتنا القادمة هي بناء النموذج النهائي باستخدام المتغيرات الاسمية وأكثر من متغير كمي.
تحويل المتغيرات
لنتذكر من رسمات الصندوق السابقة أن العمود Sex لم يكن مفيداً، لذا سنتخلص منه. سنقوم أيضاً بحذف العمود WeightAlt لأن لدينا فقط 31 منها. أخيراً، استخدام get_dummies، لتحويل البيانات الاسمية فيه BCS و Age إلى بيانات وهمية كمية لنتمكن من إدخالها إلى النموذج:
# هذا الخيار لزيادة عدد الأعمدة التي تظهر في جوبتر
pd.set_option('max_columns', 15)
X_train.drop(['Sex', 'WeightAlt'], axis=1, inplace=True)
X_train = pd.get_dummies(X_train, columns=['BCS', 'Age'])
X_train.head()
| Age_>20 | Age_<2 | Age_5-10 | Age_2-5 | Age_15-20 | Age_10-15 | BCS_4.0 | BCS_3.5 | BCS_3.0 | BCS_2.5 | BCS_2.0 | BCS_1.5 | Height | Girth | Length | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 99 | 113 | 98 | 465 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 101 | 119 | 101 | 233 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 103 | 125 | 106 | 450 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 100 | 120 | 93 | 453 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 108 | 120 | 98 | 452 |
لنتذكر أننا لاحظنا توزيع الوزن لمن أعمارهم أكبر من 5 وعدم وجود فارق كبير. لذا، سنجمع الأعمدة Age_10-15، Age_15-20، و Age_>20 إلى عمود واحد:
age_over_10 = X_train['Age_10-15'] | X_train['Age_15-20'] | X_train['Age_>20']
X_train['Age_>10'] = age_over_10
X_train.drop(['Age_10-15', 'Age_15-20', 'Age_>20'], axis=1, inplace=True)
لأننا لا نريد أن تكون المصفوفة تحتوي على متغيرات كثيره، لنقوم بحذف واحد من كلا الأعمدة الاسمية BCS و Age:
X_train.drop(['BCS_3.0', 'Age_5-10'], axis=1, inplace=True)
X_train.head()
| Age_>10 | Age_<2 | Age_2-5 | BCS_4.0 | BCS_3.5 | BCS_2.5 | BCS_2.0 | BCS_1.5 | Height | Girth | Length | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 99 | 113 | 98 | 465 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 101 | 119 | 101 | 233 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 103 | 125 | 106 | 450 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 100 | 120 | 93 | 453 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 108 | 120 | 98 | 452 |
يجب علينا إضافة عمود جديد لإظهار الانحياز في النموذج:
# اضافة عمود bias
X_train = X_train.assign(bias=1)
X_train = X_train.reindex(columns=['bias'] + list(X_train.columns[:-1]))
X_train.head()
| Age_>10 | Age_<2 | Age_2-5 | BCS_4.0 | BCS_3.5 | BCS_2.5 | BCS_2.0 | BCS_1.5 | Height | Girth | Length | bias | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 99 | 113 | 98 | 1 | 465 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 101 | 119 | 101 | 1 | 233 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 103 | 125 | 106 | 1 | 450 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 100 | 120 | 93 | 1 | 453 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 108 | 120 | 98 | 1 | 452 |
نموذج الانحدار الخطي المتعدد
نحن الآن جاهزون لضبط النموذج باستخدام جميع المتغيرات التي قررنا أنها الأهم وبعد أن حولناها لشكل مناسب للنموذج.
يمكننا تعريف نموذجنا كالتالي:
\[f_\theta (\textbf{x}) = \theta_0 + \theta_1 (Length) + \theta_2 (Girth) + \theta_3 (Height) + ... + \theta_{11} (Age\_>10)\]هذه هي الدوال التي عرفناها في درس الانحدار الخطي المتعدد، والتي سنستخدمها مرة أخرى:
def linear_model(thetas, X):
'''Returns predictions by a linear model on x_vals.'''
return X @ thetas
def mse_cost(thetas, X, y):
return np.mean((y - linear_model(thetas, X)) ** 2)
def grad_mse_cost(thetas, X, y):
n = len(X)
return -2 / n * (X.T @ y - X.T @ X @ thetas)
للقدرة على استخدام الدوال السابقة، نريد X و y. يمكننا أن نحصل عليهما من بياناتنا. تذكر أن X و y يجب أن تكون مصفوفات في NumPy لتتمكن من القيام بعملية الضرب باستخدام الرمز @:
X_train = X_train.values
y_train = y_train.values
الآن، فقط نحتاج لاستخدام الدالة minimize التي عرفناها في الجزء السابق:
thetas = minimize(mse_cost, grad_mse_cost, X_train, y_train)
theta: [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] | cost: 23979.72
theta: [0.01 0.53 0.65 0.56 0. 0. 0. 0. 0. 0. 0. 0. ] | cost: 1214.03
theta: [-0.07 1.84 2.55 -2.87 -0.02 -0.13 -0.34 0.19 0.07 -0.22 -0.3 0.43] | cost: 1002.46
theta: [-0.25 -0.76 4.81 -3.06 -0.08 -0.38 -1.11 0.61 0.24 -0.66 -0.93 1.27] | cost: 815.50
theta: [-0.44 -0.33 4.08 -2.7 -0.14 -0.61 -1.89 1.02 0.4 -1.06 -1.57 2.09] | cost: 491.91
theta: [-1.52 0.85 2. -1.58 -0.52 -2.22 -5.63 3.29 1.42 -2.59 -5.14 5.54] | cost: 140.86
theta: [-2.25 0.9 1.72 -1.3 -0.82 -3.52 -7.25 4.64 2.16 -2.95 -7.32 6.61] | cost: 130.33
theta: [ -4.16 0.84 1.32 -0.78 -1.65 -7.09 -10.4 7.82 4.18 -3.44
-12.61 8.24] | cost: 116.92
theta: [ -5.89 0.75 1.17 -0.5 -2.45 -10.36 -11.81 10.04 6.08 -3.6
-16.65 8.45] | cost: 110.37
theta: [ -7.75 0.67 1.13 -0.35 -3.38 -13.76 -11.84 11.55 8.2 -3.8
-20. 7.55] | cost: 105.74
theta: [ -9.41 0.64 1.15 -0.31 -4.26 -16.36 -10.81 11.97 10.12 -4.33
-21.88 6.15] | cost: 102.82
theta: [-11.08 0.66 1.17 -0.32 -5.18 -18.28 -9.43 11.61 11.99 -5.37
-22.77 4.69] | cost: 100.70
theta: [-12.59 0.69 1.16 -0.32 -6.02 -19.17 -8.53 10.86 13.54 -6.65
-22.89 3.73] | cost: 99.34
theta: [-14.2 0.72 1.14 -0.3 -6.89 -19.35 -8.29 10.03 14.98 -7.99
-22.74 3.14] | cost: 98.30
theta: [-16.14 0.73 1.11 -0.26 -7.94 -19.03 -8.65 9.3 16.47 -9.18
-22.59 2.76] | cost: 97.35
theta: [-18.68 0.73 1.1 -0.21 -9.27 -18.29 -9.42 8.76 18.14 -10.04
-22.55 2.39] | cost: 96.38
theta: [-21.93 0.72 1.1 -0.17 -10.94 -17.19 -10.25 8.5 19.92 -10.36
-22.66 1.99] | cost: 95.35
theta: [-26.08 0.7 1.13 -0.14 -13.03 -15.78 -10.79 8.54 21.78 -10.05
-22.83 1.59] | cost: 94.18
theta: [-31.35 0.69 1.17 -0.13 -15.59 -14.12 -10.69 8.9 23.61 -9.19
-22.93 1.32] | cost: 92.84
theta: [-37.51 0.7 1.21 -0.13 -18.44 -12.47 -9.79 9.52 25.14 -8.06
-22.78 1.38] | cost: 91.40
theta: [-43.57 0.72 1.23 -0.12 -21.06 -11.3 -8.4 10.2 25.98 -7.16
-22.24 1.87] | cost: 90.06
theta: [-48.96 0.74 1.23 -0.1 -23.13 -10.82 -7.13 10.76 26.06 -6.79
-21.34 2.6 ] | cost: 88.89
theta: [-54.87 0.76 1.22 -0.05 -25.11 -10.88 -6.25 11.22 25.55 -6.8
-20.04 3.41] | cost: 87.62
theta: [-63.83 0.78 1.21 0.02 -27.82 -11.42 -5.83 11.68 24.36 -6.96
-17.97 4.26] | cost: 85.79
theta: [-77.9 0.8 1.22 0.13 -31.81 -12.47 -6.17 12.03 22.29 -6.98
-14.93 4.9 ] | cost: 83.19
theta: [-94.94 0.81 1.26 0.23 -36.3 -13.73 -7.37 11.98 19.65 -6.47
-11.73 4.88] | cost: 80.40
theta: [-108.1 0.81 1.34 0.28 -39.34 -14.55 -8.72 11.32 17.48
-5.47 -9.92 4.21] | cost: 78.34
theta: [-115.07 0.81 1.4 0.29 -40.38 -14.75 -9.46 10.3 16.16
-4.47 -9.7 3.5 ] | cost: 77.07
theta: [-119.8 0.81 1.44 0.28 -40.43 -14.6 -9.61 9.02 15.09
-3.67 -10.25 3.05] | cost: 76.03
theta: [-125.16 0.82 1.47 0.3 -40.01 -14.23 -9.3 7.48 13.79
-3.14 -11.09 2.94] | cost: 74.96
theta: [-131.24 0.83 1.48 0.33 -39.39 -13.76 -8.71 6.21 12.41
-3.16 -11.79 3.17] | cost: 74.03
theta: [-137.42 0.84 1.48 0.39 -38.62 -13.25 -8.11 5.57 11.18
-3.67 -12.11 3.47] | cost: 73.23
theta: [-144.82 0.85 1.47 0.46 -37.36 -12.53 -7.56 5.47 9.93
-4.57 -12.23 3.56] | cost: 72.28
theta: [-155.48 0.86 1.48 0.54 -34.88 -11.3 -6.98 5.95 8.38
-5.92 -12.27 3.13] | cost: 70.91
theta: [-167.86 0.88 1.52 0.62 -31.01 -9.63 -6.53 7.03 6.9
-7.3 -12.29 1.91] | cost: 69.33
theta: [-176.09 0.89 1.57 0.64 -27.32 -8.32 -6.41 8.07 6.31
-7.84 -12.29 0.44] | cost: 68.19
theta: [-178.63 0.9 1.6 0.62 -25.15 -7.88 -6.5 8.52 6.6
-7.51 -12.19 -0.39] | cost: 67.59
theta: [-179.83 0.91 1.63 0.6 -23.4 -7.84 -6.6 8.61 7.27
-6.83 -11.89 -0.72] | cost: 67.08
theta: [-182.79 0.91 1.66 0.58 -20.55 -8.01 -6.68 8.49 8.44
-5.7 -11.11 -0.69] | cost: 66.27
theta: [-190.23 0.93 1.68 0.6 -15.62 -8.38 -6.68 8.1 10.26
-4.1 -9.46 0.01] | cost: 65.11
theta: [-199.13 0.93 1.69 0.67 -11.37 -8.7 -6.55 7.67 11.53
-3.17 -7.81 1.13] | cost: 64.28
theta: [-203.85 0.93 1.68 0.72 -10.03 -8.78 -6.42 7.5 11.68
-3.25 -7.13 1.86] | cost: 64.01
theta: [-204.24 0.93 1.67 0.74 -10.33 -8.74 -6.39 7.52 11.46
-3.52 -7.17 1.97] | cost: 63.98
theta: [-204.06 0.93 1.67 0.74 -10.48 -8.72 -6.39 7.54 11.39
-3.59 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
theta: [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95] | cost: 63.98
ونموذجنا يبدو كالتالي:
\[y = -204.03 + 0.93x_1 + ... -7.22x_{9} + 1.95x_{11}\]لنقارن هذه المعادلة التي حصلنا عليها مع أخرى قد نحصل عليها من نموذج الانحدار الخطي في مكتبة sklearn:
model = LinearRegression(fit_intercept=False)
model.fit(X_train[:, :14], y_train)
print("Coefficients", model.coef_)
Coefficients [-204.03 0.93 1.67 0.74 -10.5 -8.72 -6.39 7.54 11.39
-3.6 -7.22 1.95]
يظهر المعامل مطابقاً لما حصلنا عليه! دوالنا التي كتبناها أنتجت نفس النموذج كما لو أنتجته مكتبة بايثون!
تمكنا بنجاح من ضبط النموذج الخطي!
تقييم نموذجنا
خطوتنا التالية هي تقييم نتائج النموذج باستخدام بيانات الاختبار. نحتاج لتطبيق جميع ما فعلناه على بيانات التدريب في بيانات الاختبار قبل أن ندخلها إلى النموذج للتوقع:
X_test.drop(['Sex', 'WeightAlt'], axis=1, inplace=True)
X_test = pd.get_dummies(X_test, columns=['BCS', 'Age'])
age_over_10 = X_test['Age_10-15'] | X_test['Age_15-20'] | X_test['Age_>20']
X_test['Age_>10'] = age_over_10
X_test.drop(['Age_10-15', 'Age_15-20', 'Age_>20'], axis=1, inplace=True)
X_test.drop(['BCS_3.0', 'Age_5-10'], axis=1, inplace=True)
X_test = X_test.assign(bias=1)
X_test = X_test.reindex(columns=['bias'] + list(X_test.columns[:-1]))
X_test
| Age_>10 | Age_<2 | Age_2-5 | BCS_4.0 | BCS_3.5 | BCS_2.5 | BCS_2.0 | BCS_1.5 | Height | Girth | Length | bias | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 103 | 119 | 98 | 1 | 490 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 105 | 114 | 86 | 1 | 75 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 101 | 114 | 94 | 1 | 352 |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 102 | 114 | 94 | 1 | 182 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 105 | 113 | 104 | 1 | 334 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 110 | 124 | 104 | 1 | 543 |
108 rows × 12 columns
نقوم بإدخال X_test إلى predict في نموذجنا الخطي LinearRegression:
X_test = X_test.values
predictions = model.predict(X_test)
الآن لنطلع على نتيجة الخطأ التربيعي المتوسط:
mse_test_set(predictions)
7261.974205350604
بهذه التوقعات، يمكننا رسم نتيجة الفارق بين التوقع مقارنة بالنتائج الحقيقية Residual plot:
y_test = y_test.values
resid = y_test - predictions
resid_prop = resid / y_test
plt.scatter(np.arange(len(resid_prop)), resid_prop, s=15)
plt.axhline(0)
plt.title('Residual proportions (resid / actual Weight)')
plt.xlabel('Index of row in data')
plt.ylabel('Error proportion');
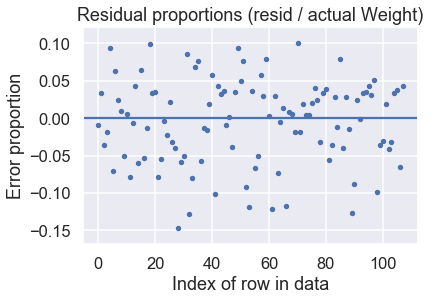
يبدو أن النموذج يؤدي بشكل رائع! نتيجة الفارق بين التوقع والنتائج الحقيقية تظهر أن توقعنا كان بحد أعلى 15% من النتيجة الحقيقية.